Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-21T09:38:49.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of Solutions for Harmonic Functions With Neumann Boundary Value

Published online by Cambridge University Press:  20 November 2018

Tao Zhang  and
Chunqin Zhou
Tao Zhang
Affiliation:
School of Mathematical Sciences, Shanghai Jiaotong University, 200240, Shanghai, China, e-mail: [email protected]
Chunqin Zhou
Affiliation:
School of Mathematical Sciences, Shanghai Jiaotong University, 200240, Shanghai, China, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we classify all solutions of

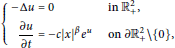$$\left\{ \begin{align} & -\Delta u=0\,\,\,\,\,\,\,\,\,\text{in}\,\,\,\mathbb{R}_{+}^{2}, \\ & \frac{\partial u}{\partial t}=-c{{\left| x \right|}^{\beta }}{{e}^{u}}\,\,\,\text{on}\,\,\partial \mathbb{R}_{+}^{2}\backslash \left\{ 0 \right\}, \\ \end{align} \right.$$

with the finite conditions

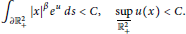$${{\int }_{\partial \mathbb{R}_{+}^{2}}}|x{{|}^{\beta }}{{e}^{u}}\,ds\,<\,C,\,\,\,\,\frac{\sup }{\mathbb{R}_{+}^{2}}\,u(x)\,<\,C.$$

Here $c$ is a positive number and 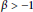$\beta \,>\,-1$.

Keywords

35A0535J65Neumann problemsingular coeffcientclassification of solutions
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 438 - 448
Copyright
Copyright © Canadian Mathematical Society 2018

References

[ADN] Agmon, S., Douglis, A., and Nirenberg, L., Estimates near the boundary for Solutions ofelliptic partial differential equations satisfying general boundary conditions. I. Comm. Pure Appl. Math. 12 (1959), 623–727. http://dx.doi.org/10.1002/cpa.3160120405Google Scholar
[CK] Chanillo, S. and Kiessling, M. K.-H., Conformally invariant Systems of nonlinear PDE of Liouville type. Geom. Funct. Anal. 5 (1995), 924–947. http://dx.doi.org/10.1007/BF01902215Google Scholar
[CL] Chen, W. and Li, C., Classification of Solutions ofsome nonlinear elliptic equations. Duke Math. J. 63(1991),615–622. http://dx.doi.org/10.1215/S0012-7094-91-06325-8Google Scholar
[JAP] Galvez, Jose A., Jimenez, Asun, and Mira, Pablo, The geometric Neumann problem for the Liouville equation. Calc. Var. Partial Differential Equations 44(2012), no. 3-4, 577–599. http://dx.doi.org/10.1007/s00526-011-0445-4Google Scholar
[JWZ] Jost, J., Wang, G. F., and Zhou, C. Q., Metrics of constant curvature on a Riemann surface with two corners on the boundary. Ann. Inst. H. Poincare Anal. Non Lineaire 26 (2009), 437–456. http://dx.doi.Org/10.1016/j.anihpc.2007.11.001Google Scholar
[Li] Liu, P., A Moser-Trudinger type inequality and blow-up analysis on Riemann surfaces. Dissertation, Der Fakultät für Mathematik and Informatik der Universität Leipzig, 2001.Google Scholar
[LZ] Li, Y. Y. and Zhu, M. J., Uniqueness theorems through the method ofmoving spheres. Duke Math. J. 80 (1995), 383–417. http://dx.doi.org/10.1215/S0012-7094-95-08016-8Google Scholar
[OB] Ou, Biao, A uniqueness theorem for harmonic functions on the upper-half plane. Conform. Geom. Dyn. 4 (2000), 120–125. http://dx.doi.org/10.1090/S1088-4173-00-00067-9Google Scholar
[PT] Prajapat, J. and Tarantello, G., On a class ofelliptic problems in R2: symmetry and uniqueness results. Proc. Roy. Soc. Edinburgh Sect. A, 131 (2001), 967–985. http://dx.doi.Org/10.1017/S0308210500001219Google Scholar
[Tl] Troyanov, M., Prescribing curvature on compact surfaces with conical singularities. Trans. Amer. Math. Soc. 324 (1991), 793–821. http://dx.doi.Org/10.1090/S0002-9947-1991-1005085-9Google Scholar
[T2] Troyanov, M., Metrics of constant curvature on a sphere with two conical singularities. In: Differential geometry. Lecture Notes in Math., 1410. Springer, Berlin, 1989, pp. 296–308. http://dx.doi.org/10.1007/BFb0086431Google Scholar
[WZ] Wang, G. and Zhu, X., Extremal Hermitian metrics on Riemann surfaces with singularities. Duke Math. J. 104 (2000), 181–209. http://dx.doi.org/10.1215/S0012-7094-00-10421-8Google Scholar
[KW] Wehrheim, Katrin, Uhlenbeck compactness, European Mathematical Society, Zürich, 2004. http://dx.doi.org/10.4171/004Google Scholar
[ZL] Zhang, Lei, Classification of conformal metrics in R\ with constant Gauss curvature and geodesic curvature on the boundary under various integralfiniteness assumptions. Calc. Var. 16 (2003), 405–430. http://dx.doi.org/10.1007/s0052 601001 55Google Scholar