Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T12:18:23.789Z Has data issue: false hasContentIssue false
  • English
  • Français

The Allison–Faulkner construction of 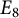$E_8$

Part of: Linear algebraic groups and related topics Other nonassociative rings and algebras Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  10 September 2021

Victor Petrov Open the ORCID record for Victor Petrov [Opens in a new window]  and
Simon W. Rigby Open the ORCID record for Simon W. Rigby [Opens in a new window]
Victor Petrov
Affiliation:
St. Petersburg State University, 29B Line 14th (Vasilyevsky Island), 199178St. Petersburg, Russia PDMI RAS, Nab. Fontanki 27, 191023St. Petersburg, Russia
Simon W. Rigby
Affiliation:
Department of Mathematics, Algebra and Geometry, Ghent University, Krijgslaan 281, 9000Ghent, Belgium e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the Tits index 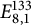$E_{8,1}^{133}$ cannot be obtained by means of the Tits construction over a field with no odd degree extensions. The proof uses a general method coming from the theory of symmetric spaces. We construct two cohomological invariants, in degrees 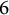$6$ and $8$ , of the Tits construction and the more symmetric Allison–Faulkner construction of Lie algebras of type 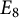$E_8$ and show that these invariants can be used to detect the isotropy rank.

Keywords

Exceptional algebraic groupsTits constructionstructurable algebras

MSC classification

Primary: 20G41: Exceptional groups
Secondary: 17B25: Exceptional (super)algebras 17D99: None of the above, but in this section
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 686 - 701
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by RFBR grant 19-01-00513. The second author was supported by FWO project G004018N.

References

Allison, B. N., A class of nonassociative algebras with involution containing the class of Jordan algebras . Math. Ann. 237(1978), no. 2, 133–156.CrossRefGoogle Scholar
Allison, B. N., Tensor products of composition algebras, Albert forms and some exceptional simple Lie algebras . Trans. Amer. Math. Soc. 306(1988), no. 2, 667–695.CrossRefGoogle Scholar
Allison, B. N., Construction of $3\times 3$ , -matrix Lie algebras and some Lie algebras of type ${D}_4$ . J. Algebra. 143(1991), 63–92.10.1016/0021-8693(91)90252-4CrossRefGoogle Scholar
Allison, B. N. and Faulkner, J. R., Nonassociative coefficient algebras for Steinberg unitary Lie algebras . J. Algebra. 161(1993), no. 1, 1–19.10.1006/jabr.1993.1202CrossRefGoogle Scholar
Allison, B. N. and Hein, W., Isotopes of some nonassociative algebras with involution . J. Algebra. 69(1981), no. 1, 120–142.CrossRefGoogle Scholar
De Clercq, C. and Garibaldi, S., On the tits p-indexes of semisimple algebraic groups. J. Lond. Math. Soc. 95(2017), 567–585.10.1112/jlms.12025CrossRefGoogle Scholar
Demazure, M. and Grothendieck, A., Structure des schémas en groupes réductifs, Lecture Notes in Mathematics, Springer, Berlin, 1970.CrossRefGoogle Scholar
Garibaldi, S., Orthogonal involutions on algebras of degree 16 and the Killing form of ${E}_8$ . In: Baeza, R., Chan, W. K., Hoffmann, D. W., Schulze-Pillot, R. (eds.), Quadratic forms–algebra, arithmetic, and geometry, Contemporary Mathematics, 493, Amer. Math. Society, Providence, RI, 2007, pp. 131–162.CrossRefGoogle Scholar
Garibaldi, S., Cohomological invariants: exceptional groups and spin groups . Mem. Amer. Math. Soc. 200(2009), no. 937, 1–81.Google Scholar
Garibaldi, S. and Guralnick, R. M., Spinors and essential dimension . Compos. Math. 153(2017), no. 3, 535–556.CrossRefGoogle Scholar
Garibaldi, S., Merkurjev, A., and Serre, J.-P., Cohomological invariants in galois cohomology, University Lecture Series, 28, American Mathematical Society (N.S.), Providence, RI, 2003.CrossRefGoogle Scholar
Garibaldi, S. and Petersson, H. P., Outer groups of type ${E}_6$ , with trivial Tits algebras. Doc. Math. 21(2016), 917–954.Google Scholar
Garibaldi, S., Petrov, V., and Semenov, N., Shells of twisted flag varieties and the Rost invariant . Duke Math. J. 165(2016), 285–339.CrossRefGoogle Scholar
Gille, P., Groupes algébriques semi-simples en dimension cohomologique $\le 2$ . Lecture Notes in Mathematics. Springer, Berlin, 2019.CrossRefGoogle Scholar
Helminck, A. and Wang, S., On rationality properties of involutions of reductive groups . Adv. Math. 99(1993), 26–96.10.1006/aima.1993.1019CrossRefGoogle Scholar
Izhboldin, O. T. and Karpenko, N. A., Some new examples in the theory of quadratic forms . Math. Z. 234(2000), no. 4, 647–695.CrossRefGoogle Scholar
Jacobson, N., Lie algebras. Dover Books on Advanced Mathematics, 10, Dover, New York, 1979.Google Scholar
Rost, M., A Pfister form invariant for étale algebras. Preprint, 2002. https://www.math.uni-bielefeld.de/~rost/data/pf-inv-et.pdf Google Scholar
Schafer, R. D., Invariant forms on central simple structurable algebras . J. Algebra. 122(1989), 112–117.CrossRefGoogle Scholar
Serre, J.-P., Cohomologie Galoisienne, Lecture Notes in Mathematics, Springer, Berlin, 1964.Google Scholar
Springer, T. A., Decompositions related to symmetric varieties . J. Algebra. 329(2011), 260–273.CrossRefGoogle Scholar
Springer, T. A. and Veldkamp, F. D., Octonions . In: Jordan algebras and exceptional groups, Springer Monographs in Mathematics, Springer, Berlin, 2000.CrossRefGoogle Scholar
Tignol, J.-P., La norme des espaces quadratiques et la forme trace des algèbres simples centrales . Publ. Math. Besançon. 3(1994), 1–18.Google Scholar
Tits, J., Algebrès alternatives, algebrès de Jordan et algebrès de Lie exceptionelles. I. Construction . Ind. Math. 28(1966), 223–237.CrossRefGoogle Scholar
Tits, J., Strongly inner anisotropic forms of simple algebraic groups . J. Algebra. 131(1990), no. 2, 648–677.CrossRefGoogle Scholar
Wittkop, T., Die Multiplikative Quadratische Norm Für Den Grothendieck-Witt-Ring. Master’s thesis, Universität Bielefeld, 2006.Google Scholar