Published online by Cambridge University Press: 18 May 2021
If the logarithmic dimension of a Cantor-type set K is smaller than 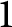 $1$
, then the Whitney space
$1$
, then the Whitney space 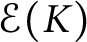 $\mathcal {E}(K)$
possesses an interpolating Faber basis. For any generalized Cantor-type set K, a basis in
$\mathcal {E}(K)$
possesses an interpolating Faber basis. For any generalized Cantor-type set K, a basis in 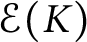 $\mathcal {E}(K)$
can be presented by means of functions that are polynomials locally. This gives a plenty of bases in each space
$\mathcal {E}(K)$
can be presented by means of functions that are polynomials locally. This gives a plenty of bases in each space 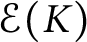 $\mathcal {E}(K)$
. We show that these bases are quasi-equivalent.
$\mathcal {E}(K)$
. We show that these bases are quasi-equivalent.
The research was partially supported by TÜBİTAK (Scientific and Technological Research Council of Turkey), Project 119F023.