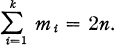A band is a closed connected set in the 2-sphere, bounded by one or more disjoint simple closed curves.
Consider a band B with bounding curves J1, J2, … , Jk. On each curve Ji let there be chosen mi ≥ 0 points to be called vertices, with the restriction that the sum of the k integers mi is to be even. Write
(1)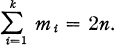
Next consider a set of n disjoint open arcs in the interior of B which join the 2n vertices in pairs and partition the remainder of the interior of B into simply connected domains. We call the resulting dissection of B a slicing with respect to the given set of vertices. The arcs are the internal edges of the slicing and the simply connected domains are its internal faces, or slices.