Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-29T00:19:20.873Z Has data issue: false hasContentIssue false
  • English
  • Français

The Gibbs Phenomenon and Lebesgue Constants for Regular Sonnenschein Matrices

Published online by Cambridge University Press:  20 November 2018

W. T. Sledd
W. T. Sledd*
Affiliation:
University of Kentucky, Michigan State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If ψ(x) is a real-valued function which has a jump discontinuity at x = ε and otherwise satisfies the Dirichlet conditions in a neighbourhood of x = ε then {sn(x)} the sequence of partial sums of the Fourier series for ψ(x) cannot converge uniformly at x = ε. Moreover, it can be shown that given τ in [ — π, π] then there is a sequence {tn} such that tn → ε and

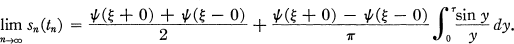
This behaviour of {sn(x)} is called the Gibbs phenomenon. If {σn(x)} is the transform of {sn(x)} by a summability method T, and if {σn(x)} also has the property described then we say that T preserves the Gibbs phenomenon.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 723 - 728
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Bajšanski, B., Sur une classe de procédés de sommations du type d'Euler-Borel, Publ. Inst. Math. Beograd, 10 (1956), 131–152.Google Scholar
2. Carslaw, H. S., Theory of Fourier's series and integrals, London (1930).Google Scholar
3. Clunie, J. and Vermes, P., Regular Sonnenschein type summability methods, Bull. Acad. Royale de Belgique (5), 45 (1959), 930–954.Google Scholar
4. Fejér, L., Lebesguesche Konstanten und Divergente Fourierreihen, J. fur die reine und angewandte Mathematik, 138 (1910), 22–53.Google Scholar
5. Hardy, G. H. and Rogosinski, W. W., Fourier series, Cambridge (1944).Google Scholar
6. Livingston, A. E., The Lebesgue constants for Ruler (E, p) summation of Fourier series, Duke Math. J., 21 (1954), 309–313.Google Scholar
7. Lorch, L., The Lebesgue constants for Borel summability, Duke Math. J., 11 (1944), 459–467.Google Scholar
8. Lorch, L., The Lebesgue constants for (E, I) summation of Fourier series, Duke Math., 19 (1952), 45–50.Google Scholar
9. Lorch, L. and Newman, D. J., The Lebesgue constants for regular Hausdorff methods, Can. J. Math., 13 (1961), 283–298.Google Scholar
10. Miracle, C. L., The Gibbs phenomenon for Taylor means and for [F, dn] means, Can. J. Math., 12 (1960), 660–673.Google Scholar
11. Sledd, W. T., Regularity conditions for Karamata matrices (to appear in J. London Math. Soc).Google Scholar
12. Sonnenschein, J., Sur les séries divergentes, Bull. Acad. Royale de Belgique, 35 (1949), 594–601.Google Scholar