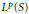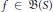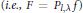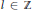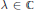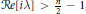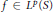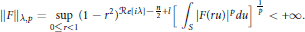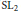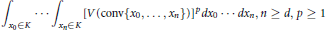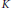Research Article
Criteria for Very Ampleness of Rank Two Vector Bundles over Ruled Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1201-1227
-
- Article
-
- You have access
- Export citation
Valuations for Matroid Polytope Subdivisions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1228-1245
-
- Article
-
- You have access
- Export citation
Quantum Cohomology of Minuscule Homogeneous Spaces III Semi-Simplicity and Consequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1246-1263
-
- Article
-
- You have access
- Export citation
Holomorphic Variations of Minimal Disks with Boundary on a Lagrangian Surface
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1264-1275
-
- Article
-
- You have access
- Export citation
A Generalized Poisson Transform of an Lp-Function over the Shilov Boundary of the n-Dimensional Lie Ball
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1276-1292
-
- Article
-
- You have access
- Export citation
Canonical Toric Fano Threefolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1293-1309
-
- Article
-
- You have access
- Export citation
Iwahori-Hecke Algebras of SL2 over 2-Dimensional Local Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1310-1324
-
- Article
-
- You have access
- Export citation
On Some Explicit Constructions of Finsler Metrics with Scalar Flag Curvature
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1325-1339
-
- Article
-
- You have access
- Export citation
Holomorphie des opérateurs d’entrelacement normalisés à l’aide des paramètres d’Arthur
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1340-1386
-
- Article
-
- You have access
- Export citation
Homotopy Self-Equivalences of 4-manifolds with Free Fundamental Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1387-1403
-
- Article
-
- You have access
- Export citation
Characterizations of Extremals for some Functionals on Convex Bodies
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1404-1418
-
- Article
-
- You have access
- Export citation
BMO-Estimates for Maximal Operators via Approximations of the Identity with Non-Doubling Measures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1419-1434
-
- Article
-
- You have access
- Export citation