A Generalized Poisson Transform of an L^p-Function over the Shilov Boundary of the n-Dimensional Lie Ball

Abstract

Let 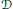$D$ be the $n$-dimensional Lie ball and let 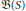$B\text{(S)}$ be the space of hyperfunctions on the Shilov boundary $S$ of 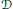$D$. The aim of this paper is to give a necessary and sufficient condition on the generalized Poisson transform 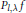${{P}_{l,\text{ }\!\!\lambda\!\!\text{ }}}f$ of an element 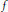$f$ in the space 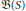$B\text{(S)}$ for 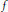$f$ to be in 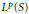${{L}^{p}}\left( S \right)$, $1\,<\,p\,<\,\infty $. Namely, if $F$ is the Poisson transform of some 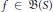$f\in \,B(S)$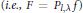$F\,=\,{{P}_{l,\lambda }}f$), then for any 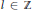$l\,\in \,Z$) and 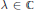$\lambda \,\in \,C$ such that 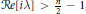$Re[\text{i}\lambda ] > \frac{n}{2}\,-\,1$, we show that 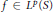$f\,\in \,{{L}^{p}}\text{(}S\text{)}$ if and only if 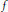$f$ satisfies the growth condition

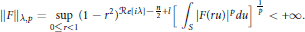$${{\left\| F \right\|}_{\lambda ,p}}=\underset{0\le r<1}{\mathop{\sup }}\,{{\left( 1\,-\,{{r}^{2}} \right)}^{\operatorname{Re}\left[ \text{i }\lambda \text{ } \right]-\frac{n}{2}+l}}{{\left[ \,\int_{s}{{{\left| F\left( ru \right) \right|}^{p}}du} \right]}^{\frac{1}{p}}}<\,+\infty $$