Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-04T19:09:09.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Semidirect Product Compactifications

Published online by Cambridge University Press:  20 November 2018

F. Dangello  and
R. Lindahl
F. Dangello
Affiliation:
Shippensburg State College, Shippensburg, Pennsylvania
R. Lindahl
Affiliation:
Morehead State University, Morehead, Kentucky
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. K. Deleeuw and I. Glicksberg [4] proved that if S and T are commutative topological semigroups with identity, then the Bochner almost periodic compactification of S × T is the direct product of the Bochner almost periodic compactifications of S and T. In Section 3 we consider the semidirect product of two semi topological semigroups with identity and two unital C*-subalgebras 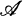and 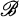of W(S) and W(T) respectively, where W(S) is the weakly almost periodic functions on S. We obtain necessary and sufficient conditions 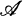and 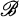for a semidirect product compactification of to exist such that this compactification is a semi topological semigroup and such that this compactification is a topological semigroup. Moreover, we obtain the largest such compactifications.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 1 , 01 February 1983 , pp. 1 - 32
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Berglund, J. F., Junghenn, H. D. and Milnes, P., Compact right topological semigroups and generalizations of almost periodicity (Springer-Verlag, New York, 1978).Google Scholar
2. Berglund, J. F. and Milnes, P., Algebras of functions on semi-topological left-groups, Trans. Amer. Math. Soc. 222 (1976), 157–178.Google Scholar
3. Burckel, R. B., Weakly almost periodic functions on semigroups (Gordon and Breach, New York, 1970).Google Scholar
4. Deleeuw, K. and Glicksberg, I., Almost periodic functions on semigroups, Acta Math. 105 (1961), 99–140.Google Scholar
5. Deleeuw, K. and Glicksberg, I., Applications of almost periodic compactifications, Acta Math. 105 (1961), 63–97.Google Scholar
6. Edwards, R., Functional analysis (Holt, Rinehart, and Winston, New York, 1965).Google Scholar
7. Ellis, R., Locally compact transformation groups, Duke Math. J. 24 (1957), 119–125.Google Scholar
8. Grothendieck, A., Critères de compacité dans les espaces fonctionnels généraux, Amer. J. Math. 74 (1952), 168–186.Google Scholar
9. Hewitt, E. and Ross, K. A., Abstract harmonie analysis I (Academic Press, New York, 1963).Google Scholar
10. Junghenn, H. D., Almost periodic compactifications of transformation semigroups, Pacific J. Math. 57 (1975), 207–216.Google Scholar
11. Junghenn, H. D., Almost periodic functions on semidirect products of transformation semigroups, Pacific J. Math. 79 (1978), 117–128.Google Scholar
12. Junghenn, H. D., C*-algebras of functions on direct products of semigroups, Rocky Mountain J. Math. 10 (1980), 589–597.Google Scholar
13. Junghenn, H. D., Tensor products of spaces of almost periodic functions, Duke Math J. 41 (1974), 661–666.Google Scholar
14. Junghenn, H. D. and Lerner, B. T., Semigroup compactifications of semidirect products, Trans. Amer. Math. Soc. 265 (1981), 393–404.Google Scholar
15. Landstad, M., On the Bohr compactification of a transformation group, Math. Zeit. 127 (1972), 167–178.Google Scholar
16. Milnes, P., Semigroup compactifications of direct and semidirect products, Preprint.Google Scholar
17. Mitchell, T., Function algebras, means, and fixed points, Trans. Amer. Math. Soc. 130 (1968), 117–126.Google Scholar
18. Rickart, C. R., General theory of Banach algebras (D. Van Nostrand, Princeton, N.J., 1960).Google Scholar
19. Schatten, R., A theory of cross-spaces (Ann. of Math. Studies, Princeton University Press, Princeton, N.J., 1950).Google Scholar
20. Troallic, J.-P., Fonctions à valeurs dans des espaces fonctionnels généraux: théorèmes de R. Ellis et de I. Namioka, C. R. Acad. Se. Paris 287 (1978), 63–66.Google Scholar