Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T05:18:48.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of Regular ParametrizedOne-relation Operads

Published online by Cambridge University Press:  20 November 2018

Murray Bremner  and
Vladimir Dotsenko
Murray Bremner
Affiliation:
Department of Mathematics and Statistics, University of Saskatchewan, 106 Wiggins Road, S7M 5E6, Saskatoon, Saskatchewan e-mail: [email protected]
Vladimir Dotsenko
Affiliation:
School of Mathematics, Trinity College Dublin, College Green, Dublin 2, Ireland and Departamento de Matemáticas, CINVESTAV-IPN, Av., Instituto Politécnico Nacional 2508, Col. San Pedro Zacatenco, México, D.F., CP 07360, Mexico e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Jean-Louis Loday introduced a class of symmetric operads generated by one bilinear operation subject to one relation making each left-normed product of three elements equal to a linear combination of right-normed products: $({{a}_{1}}{{a}_{2}}){{a}_{3}}\,=\,\sum{{{_{\sigma }}_{\in {{s}_{3}}}}\,}{{x}_{\sigma }}\,{{a}_{\sigma \,(1)}}({{a}_{\sigma (2)\,}}{{a}_{\sigma (3)}})$. Such an operad is called a parametrized one-relation operad. For a particular choice of parameters 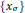$\{{{x}_{\sigma }}\}$, this operad is said to be regular if each of its components is the regular representation of the symmetric group; equivalently, the corresponding free algebra on a vector space 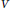$V$ is, as a graded vector space, isomorphic to the tensor algebra of 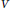$V$. We classify, over an algebraically closed field of characteristic zero, all regular parametrized one-relation operads. In fact, we prove that each such operad is isomorphic to one of the following five operads: the left-nilpotent operad defined by the relation 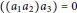$(({{a}_{1}}{{a}_{2}}){{a}_{3}})\,=\,0$, the associative operad, the Leibniz operad, the dual Leibniz (Zinbiel) operad, and the Poisson operad. Our computational methods combine linear algebra over polynomial rings, representation theory of the symmetric group, and Gröbner bases for determinantal ideals and their radicals.

Keywords

18D5013B2513P1013P1515A5417-0417A3017A5020C3068W30parametrized one-relation algebraalgebraic operadKoszul dualityrepresentation theory of the symmetric groupdeterminantal idealGröbner basis
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 5 , 01 October 2017 , pp. 992 - 1035
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Albert, A. A., Power-associative rings. Trans. Amer. Math. Soc. 64(1948), 552–593.http://dx.doi.org/10.1090/S0002-9947-1948-0027750-7 Google Scholar
[2] Bergman, G. M., The diamond lemma for ring theory. Adv. in Math. 29(1978), no. 2,178–218.http://dx.doi.Org/10.1016/0001-8708(78)90010-5 Google Scholar
[3] Boocher, A., Free resolutions and sparse determinantal ideals. Math. Res. Lett. 19(2012), no. 4, 805–821.http://dx.doi.Org/10.4310/MRL.2012.v1 9.n4.a6 Google Scholar
[4] Bosma, W., Cannon, J., and Playoust, C., The Magma algebra system. I. The user language. J. Symbolic Comput, 24(1997), 235–265.http://dx.doi.Org/10.1006/jsco.1996.0125 Google Scholar
[5] Bremner, M. R. and Dotsenko, V., Algebraic operads: an algorithmic companion. To appear: Chapman and Hall / CRC Press, 2016.Google Scholar
[6] Bremner, M. R., Online addendum to the article “Classification of regular parametrized one-relation operads”. Available via the http://www.maths.tcd.ie/~vdots/BDaddendum.pdf, along with the copy-pasteable Magma script http://www.maths.tcd.ie/~vdots/BDaddendum.txt. Google Scholar
[7] Bremner, M. R., Madariaga, S., and Peresi, L. A., Structure theory for the group algebra of the symmetric group, with applications to polynomial identities for the octonions. Comment. Math. Univ. Carolin. 57(2016), no. 4, 413–452.Google Scholar
[8] Clifton, J. M., A simplification of the computation of the natural representation of the symmetric group Sn. Proc. Amer. Math. Soc. 83(1981), no. 2, 248–250.Google Scholar
[9] Cox, D., Little, J., and O'Shea, D., Ideals, varieties, and algorithms: an introduction to computational algebraic geometry and commutative algebra. 3rd ed. Undergraduate Texts in Mathematics, 3. Springer, New York, 2007. http://dx.doi.org/10.1007/978-0-387-35651-8 Google Scholar
[10] Cox, D., Using algebraic geometry. 2nd ed. Graduate Texts in Mathematics, 185. Springer, New York, 2005.Google Scholar
[11] Dotsenko, V. and Khoroshkin, A., Gröbner bases for operads. Duke Math. J. 153(2010), no. 2, 363–396.http://dx.doi.org/10.1215/00127094-2010-026 Google Scholar
[12] Drinfel'd, V. G., On quadratic commutation relations in the quasiclassical case. Selecta Math. Soviet. 11(1992), no. 4, 317–326.Google Scholar
[13] Ginzburg, V., and Kapranov, M., Koszul duality for operads. Duke Math. J. 76(1994), no. 1, 203–272.http://dx.doi.org/10.1215/S0012-7094-94-07608-4 Google Scholar
[14] Livernet, M., Dualité de Koszul pour les opérades quadratiques binaires. M.Sc. thesis, Université de Strasbourg, 1995.Google Scholar
[15] Loday, J.-L. and Vallette, B., Algebraic operads. Grundlehren der Mathematischen Wissenschaften, 346. Springer, Heidelberg, 2012.Google Scholar
[16] Magma Calculator, http://magma.maths.usyd.edu.au/calc/. Google Scholar
[17] Markl, M. and Remm, E., Algebras with one operation including Poisson and other Lie-admissible algebras. J. Algebra 299(2006), no. 1,171–189.http://dx.doi.Org/10.1016/j.jalgebra.2OO5.O9.O18 Google Scholar
[18] Markl, M., (Non-)Koszulness of operads for n-ary algebras, galgalim and other curiosities. J. Homotopy Relat. Struct. 10(2015) no. 4, 939–969.http://dx.doi.Org/10.1007/s40062-014-0090-7 Google Scholar
[19] Miro-Roig, R. M., Determinantal deals. Progress in Mathematics, 264. Birkhäuser Verlag, Basel, 2008.Google Scholar
[20] Polishchuk, A. and Positselski, L., Quadratic algebras. American Mathematical Society, Providence, RI, 2005.http://dx.doi.Org/10.1090/ulect/037 Google Scholar
[21] Stanley, R. P., Catalan numbers. Cambridge University Press, New York, 2015.http://dx.doi.Org/10.1017/CBO9781139871 495 Google Scholar
[22] Zinbiel, G. W., Encyclopedia of types of algebras 2010. In: Operads and universal algebra. World Scientific Publishing, Hackensack, NJ, 2012, pp. 217–297. http://dx.doi.org/10.1142/978981 4365123J3O11 Google Scholar