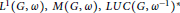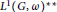Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
DABHI, PRAKASH A.
and
LIKHADA, DARSHANA B.
2021.
ON ALGEBRA ISOMORPHISMS BETWEEN p-BANACH BEURLING ALGEBRAS.
Bulletin of the Australian Mathematical Society,
Vol. 104,
Issue. 2,
p.
308.
Kuznetsova, Yulia
and
Zadeh, Safoura
2021.
On isomorphisms between weighted
-algebras.
Canadian Mathematical Bulletin,
Vol. 64,
Issue. 4,
p.
853.
Kroeker, Matthew E.
Stephens, Alexander
Stokke, Ross
and
Yee, Randy
2022.
Norm-multiplicative homomorphisms of Beurling algebras.
Journal of Mathematical Analysis and Applications,
Vol. 509,
Issue. 1,
p.
125935.
Tabatabaie, Seyyed Mohammad
and
Latifpour, Mahdi
2023.
Isomorphisms of Orlicz spaces.
Forum Mathematicum,
Vol. 35,
Issue. 1,
p.
95.