Research Article
On subnormality of generalized derivations and tensor products
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 235-243
-
- Article
-
- You have access
- Export citation
A note on arewise connected sets and functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-375
-
- Article
-
- You have access
- Export citation
On the zeros of a polynomial and its derivative
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 245-255
-
- Article
-
- You have access
- Export citation
The minimal number of periodic orbits of periods guaranteed in Sharkovskii's theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 89-103
-
- Article
-
- You have access
- Export citation
Irreducible designs from supplementary difference sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 105-115
-
- Article
-
- You have access
- Export citation
The subvariety lattice of the variety of distributive double p-algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-387
-
- Article
-
- You have access
- Export citation
On the radical theory of Andrunakievich varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 257-269
-
- Article
-
- You have access
- Export citation
Trajectories of set valued integrals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 389-411
-
- Article
-
- You have access
- Export citation
Antipodal coincidence sets and stronger forms of connectedness
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 271-284
-
- Article
-
- You have access
- Export citation
Weighted composition operators on functional Hilbert spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 117-126
-
- Article
-
- You have access
- Export citation
Oscillatory behavior of nonlinear differential equations with deviating arguments
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 127-136
-
- Article
-
- You have access
- Export citation
A note on spaces related to Namioka spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 285-292
-
- Article
-
- You have access
- Export citation
A crossing theorem for distribution functions and their moments
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 413-419
-
- Article
-
- You have access
- Export citation
Some results concerning the Cauchy functional equation in certain Banach algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-144
-
- Article
-
- You have access
- Export citation
On convergence of closed sets in a metric space and distance functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-432
-
- Article
-
- You have access
- Export citation
Bilateral approximations and periodic solutions of systems of differential equations with impulses
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-307
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Algorithms and application for special classes of nonlinear least squares problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 309-311
-
- Article
-
- You have access
- Export citation
Research Article
On the basis number of some complete bipartite graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-437
-
- Article
-
- You have access
- Export citation
On the laws of certain varieties of groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-154
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Protein folding
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-314
-
- Article
-
- You have access
- Export citation

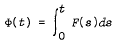 , where the set valued integral is interpreted in the sense of Aumann. We study the topological and algebraic properties of
, where the set valued integral is interpreted in the sense of Aumann. We study the topological and algebraic properties of 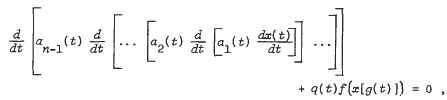
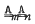 (consisting of all groups
(consisting of all groups 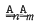 both satisfy the following three laws:
both satisfy the following three laws: