Article contents
Trajectories of set valued integrals
Published online by Cambridge University Press: 17 April 2009
Abstract
The purpose of this paper is to study the trajectory multifunction Φ(·) determined by the indefinite set valued integral of a measurable Banach space valued multifunction F(·), that is for all t ∈ [0, T], 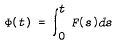 , where the set valued integral is interpreted in the sense of Aumann. We study the topological and algebraic properties of SΦ equaling the set of selectors of Φ(·) whose primitive is an integrable selector of F(·). We also determine several useful properties that Φ(·) possesses and finally we present some convergence and stability results using the Kuratowski-Mosco convergence of sets.
, where the set valued integral is interpreted in the sense of Aumann. We study the topological and algebraic properties of SΦ equaling the set of selectors of Φ(·) whose primitive is an integrable selector of F(·). We also determine several useful properties that Φ(·) possesses and finally we present some convergence and stability results using the Kuratowski-Mosco convergence of sets.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1985
References
- 3
- Cited by


