Research Article
Notes on irreducible ideals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-324
-
- Article
-
- You have access
- Export citation
Wilansky's query on outer measures
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 325-328
-
- Article
-
- You have access
- Export citation
On the discrepancy of the sequence formed from multiples of an irrational number
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-338
-
- Article
-
- You have access
- Export citation
Intersections of finitely generated free groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 339-348
-
- Article
-
- You have access
- Export citation
Indecomposable 2-groups with all automorphisms central
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 349-354
-
- Article
-
- You have access
- Export citation
Normal and subnormal subgroups in the group of units of group rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 355-363
-
- Article
-
- You have access
- Export citation
On a commutativity theorem for semi-simple rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 365-368
-
- Article
-
- You have access
- Export citation
A note on arewise connected sets and functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-375
-
- Article
-
- You have access
- Export citation
The subvariety lattice of the variety of distributive double p-algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-387
-
- Article
-
- You have access
- Export citation
Trajectories of set valued integrals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 389-411
-
- Article
-
- You have access
- Export citation
A crossing theorem for distribution functions and their moments
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 413-419
-
- Article
-
- You have access
- Export citation
On convergence of closed sets in a metric space and distance functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-432
-
- Article
-
- You have access
- Export citation
On the basis number of some complete bipartite graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-437
-
- Article
-
- You have access
- Export citation
Periodic points and chaos for expanding self-maps of the interval
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 439-443
-
- Article
-
- You have access
- Export citation
The Farkas lemma of Shimizu, Aiyoshi and Katayama
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 445-450
-
- Article
-
- You have access
- Export citation
An Egerev's theorem for vector functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 451-462
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Eigenvalue approximation methods for quantum lattice Hamiltonians
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 463-465
-
- Article
-
- You have access
- Export citation
Unattained boundary points of the numerical range of Hilbert space operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 467-469
-
- Article
-
- You have access
- Export citation
Chain decompositions of graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 471-473
-
- Article
-
- You have access
- Export citation
Intersection properties of functions on cardinals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 475-477
-
- Article
-
- You have access
- Export citation

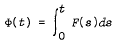 , where the set valued integral is interpreted in the sense of Aumann. We study the topological and algebraic properties of
, where the set valued integral is interpreted in the sense of Aumann. We study the topological and algebraic properties of