Research Article
On the complex complementarity problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-257
-
- Article
-
- You have access
- Export citation
Connected expansions of topologies
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-265
-
- Article
-
- You have access
- Export citation
On categorical semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 61-68
-
- Article
-
- You have access
- Export citation
Hermite-Fejer interpolation at the ‘practical’ Chebyshev nodes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 379-390
-
- Article
-
- You have access
- Export citation
Macroscopic descriptions of microscopic phenomena
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-410
-
- Article
-
- You have access
- Export citation
The zero divisor question for supersolvable groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 69-71
-
- Article
-
- You have access
- Export citation
Finite groups which are the product of two nilpotent subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-274
-
- Article
-
- You have access
- Export citation
Characters for summary functions associated with cartesian products
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 411-415
-
- Article
-
- You have access
- Export citation
On rings with trivial torsion parts
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 275-290
-
- Article
-
- You have access
- Export citation
The algebra of functions with Fourier transforms in a given function space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 73-82
-
- Article
-
- You have access
- Export citation
Transient development of capillary-gravity waves in a running stream
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 417-432
-
- Article
-
- You have access
- Export citation
Invariant metrics on free topological groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-88
-
- Article
-
- You have access
- Export citation
A converse of Bernstein's inequality for locally compact groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-298
-
- Article
-
- You have access
- Export citation
Computer results on Burnside groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-438
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
A discrete analytic theory of geometric difference functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-300
-
- Article
-
- You have access
- Export citation
Research Article
Quasi proximal continuity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 89-98
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Minimal number of generators of some classes of groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 301-302
-
- Article
-
- You have access
- Export citation
Research Article
A useful relationship in the conformal mapping of quadrilaterals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 99-104
-
- Article
-
- You have access
- Export citation
An application of combinatorial techniques to a topological problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 439-443
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Orthogonal transformations and improperly posed problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 303-304
-
- Article
-
- You have access
- Export citation

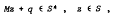
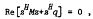
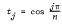 , 0(1)
, 0(1)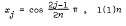 , 1(1)
, 1(1)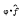 is Fourier transform of an
is Fourier transform of an 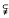
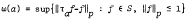
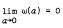 , then
, then  is relatively compact (where Σ(
is relatively compact (where Σ(