Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-04T20:09:03.244Z Has data issue: false hasContentIssue false
  • English
  • Français

The algebra of functions with Fourier transforms in a given function space

Published online by Cambridge University Press:  17 April 2009

U.B. Tewari  and
A.K. Gupta
U.B. Tewari
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kanpur, India.
A.K. Gupta
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kanpur, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a locally compact abelian group and Ĝ be its dual group. For 1 ≤ p < ∞, let Ap (G) denote the set of all those functions in L1(G) whose Fourier transforms belong to Lp (Ĝ). Let M(Ap (G)) denote the set of all functions φ belonging to L∞(Ĝ) such that 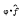is Fourier transform of an L1-function on G whenever f belongs to Ap (G). For 1 ≤ p < q < ∞, we prove that Ap (G) 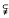Aq(G) provided G is nondiscrete. As an application of this result we prove that if G is an infinite compact abelian group and 1 ≤ p ≤ 4 then lp (Ĝ) 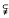M(Ap(G)), and if p > 4 then there exists ψ є lp (Ĝ) such that ψ does not belong to M(Ap (G)).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 9 , Issue 1 , August 1973 , pp. 73 - 82
Copyright
Copyright © Australian Mathematical Society 1973

References

[1]Edwards, R.E., “Changing signs of Fourier coefficients”, Pacific J. Math. 15 (1965), 463–475.CrossRefGoogle Scholar
[2]Edwards, R.E., Fourier series: A modern introduction, Volume II (Holt, Rinehart and Winston, New York, Chicago, San Francisco, Atlanta, Dallas, Montreal, Toronto, London, 1967).Google Scholar
[3]Edwards, R.E., “Inequalities related to those of Hausdorff-Young”, Bull. Austral. Math. Soc. 6 (1972), 185–210.CrossRefGoogle Scholar
[4]Goldberg, P.R., Fourier transforms (Cambridge Tracts in Mathematics and Mathematical Physics, 52. Cambridge University Press, Cambridge, 1961).Google Scholar
[5]Hewitt, Edwin and Ross, Kenneth A., Abstract harmonic analysis, Volume I (Die Grundlehren der mathematischen Wissenschaften, Band 115. Academic Press, New York; Springer-Verlag, Berlin, Göttingen, Heidelberg., 1963).Google Scholar
[6]Hewitt, Edwin and Ross, Kenneth A., Abstract harmonic analysis, Volume II (Die Grundlehren der mathematischen Wissenschaften, Band 152. Springer-Verlag, Berlin, Heidelberg, New York, 1970).Google Scholar
[7]Larsen, Ronald, An introduction to the theory of multipliers (Die Grundlehren der mathematischen Wissenschaften, Band 175. Springer-Verlag, Berlin, Heidelberg, New York, 1971).CrossRefGoogle Scholar
[8]Larsen, Ronald, “The multipliers for functions with Fourier transforms in Lp”, Math. Scand. 28 (1971), 215–225.CrossRefGoogle Scholar
[9]Martin, John C. and Yap, Leonard Y.H., “The algebra of functions with Fourier transforms in Lp”, Proc. Amer. Math. Soc. 24 (1970), 217–219.Google Scholar
[10]Reiter, Hans, Classical harmonic analysis and locally compact groups (Clarendon Press, Oxford, 1968).Google Scholar
[11]Reiter, Hans, L1-algebras and Segal algebras (Lecture Notes in Mathematics, 231. Springer-Verlag, Berlin, Heidelberg, New York, 1971).CrossRefGoogle Scholar
[12]Rudin, Walter, Fourier analysis on groups (Interscience, New York, London, 1962).Google Scholar