The natural, first order version of Peano's axioms (the theory T with 0, the successor function and an induction schema) is shown to possess the following nonstandard model: the natural numbers together with a collection of ‘infinite’ elements isomorphic to the integers. In fact, a complete list of the models of this theory is obtained by showing that T is equivalent to the apparently weaker theory with the induction axiom replaced by axioms stating that there are no finite cycles under the successor function and that 0 is the only non-successor.

A solution is given for un + 1 in terms of u1 and u0, where the elements of the sequence {un} satisfy the linear difference equation

Two linearly independent solutions of the equation are written as determinants and relations are given which can be used to check the evaluation of these determinants.

Let α1, …, αm be distinct complex numbers and τ(1), …, τ(m) be non-negative integers. We obtain conditions under which the functions

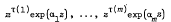
form a perfect system, that is, for every set ρ(1), …, ρ(m) of non-negative integers, there are polynomials a1 (z), …, am (z) with respective degrees exactly ρ(1)−1, …, ρ(m)−1, such that the function

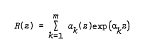
has a zero of order at least ρ(1) + … + ρ(m)−1 at the origin. Moreover, subject to the evaluation of certain determinants, we give explicit formulae for the approximating polynomials a1 (z), …, am (z).

This paper gives convergence properties and applications of the discrete analogs of reproducing kernels for various families of harmonic functions. From these results information is obtained on the solution of interpolation problems, the convergence of the discrete Neumann's function, and the solution to problems involving the discrete biharmonic operator.

Kaplansky's observation, namely, a commutative ring R is (von Neumann) regular if and only if each simple R-module is injective, is generalized to projective modules over a commutative ring.

It is shown how torsionfree modules can be used to characterize certain important classes of orders over Dedekind rings. In particular, we show that an order is Gorenstein if and only if each of its lattices can be embedded as a pure sublattice of a free lattice. We also show that an order is hereditary if and only if the tensor product of any of its right lattices with any of its left lattices is torsionfree over the ground domain.

Multivariate versions of Mercer's Theorem and the usual expansions of the resolvent and Fredholm determinant are shown to hold for an n × n symmetric kernel N(x, y) with arbitrary domain in Rp under weakened continuity conditions. Further, the resolvent and determinant of N(x, y) − a(x)b(y) are given in terms of those of N(x, y).

It is shown by enumeration that for any two non-isomorphic limbs with the same number of points the number of trees with p points that contain one limb equals the number of trees with p points that contain the other.

The object of this paper is to study a stochastic discrete system, including an operator T, of the form

as a perturbation of the linear stochastic discrete system

where ω ∈ Ω, the supporting set of probability measure space (Ω, A, P) and n ∈ N, the set of nonnegative integers. We are concerned vith the existence, uniqueness, boundedness, and asymptotic behavior of random solutions of the above equation.

Let S and X be any two sets; then a mapping Γ which assigns to each point t in S a set Γ(t) of points in X is called a multifunction from S into X. A selector for Γ is a function f from S into X such that f(t) ∈ Γ(t) for each t. We introduce here a class of multifunctions which is both well-supplied with measurable selectors and yet is comprehensive enough to include those kinds of multifunction which have been most commonly studied before. Hence in order to show that a multifunction with non-empty values, which may arise naturally in an implicit function problem, has a measurable selector, it is sufficient to show that it is of Souslin type.

A regular completion with universal property is obtained for each member of the class of u–embedded uniform convergence spaces, a class which includes the Hausdorff uniform spaces. This completion is obtained by embedding each u-embedded uniform convergence space (X, I) into the dual space of a complete function algebra composed of the uniformly continuous functions from (X, I) into the real line.

In defining the torsion-theoretic Krull dimension of an associative ring R we make use of a function δ from the complete lattice of all subsets of the torsion-theoretic spectrum of R to the complete lattice of all hereditary torsion theories on R-mod. In this note we give necessary and sufficient conditions for δ to be injective, surjective, and bijective. In particular, δ is bijective if and only if R is a left semiartinian ring.

Let G be an abelian group, and let S be a subset of G. Necessary and sufficient conditions on G and S are given in order that there should exist a Dedekind domain D with class group G with the property that S is the set of classes that contain maximal ideals of D. If G is a torsion group, then S is the set of classes containing the maximal ideals of D if and only if S generates G. These results are used to determine necessary and sufficient conditions on a family {Hλ} of subgroups of G in order that there should exist a Dedekind domain D with class group G such that {G/Hλ} is the family of class groups of the set of overrings of D. Several applications are given.

In this note some results concerning the equidistant set E(−x, x) and the kernel Mθ of the metric projection PM, where M is a Chebyshev subspace of a normed linear space X, have been obtained. In particular, when X = lp (1 < p < ∞), it has been proved that every equidistant set is closed in the bw-topology of the space. In c0 no equidistant set has this property.

It is proved that the free k-group on a CW-complex X is itself a CW-complex containing X as a subcomplex. It follows, as a corollary, that the free topological group on a countable CW-complex is a countable CW-complex.