Research Article
NILPOTENCY OF THE GROUP OF UNITS OF A FINITE RING
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2009, pp. 177-182
-
- Article
-
- You have access
- Export citation
ON SOME WEIGHTED AVERAGE VALUES OF L-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2009, pp. 183-186
-
- Article
-
- You have access
- Export citation
KRASNOSELSKI–MANN ITERATION FOR HIERARCHICAL FIXED POINTS AND EQUILIBRIUM PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2009, pp. 187-200
-
- Article
-
- You have access
- Export citation
PRODUCT FRACTAL SETS DETERMINED BY STABLE PROCESSES
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2009, pp. 201-212
-
- Article
-
- You have access
- Export citation
A POLYNOMIAL RING CONSTRUCTION FOR THE CLASSIFICATION OF DATA
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 213-225
-
- Article
-
- You have access
- Export citation
COMPACT LEFT MULTIPLIERS ON BANACH ALGEBRAS RELATED TO LOCALLY COMPACT GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 227-238
-
- Article
-
- You have access
- Export citation
EVALUATION OF CERTAIN CLASSES OF EISENSTEIN-TYPE SERIES
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 239-247
-
- Article
-
- You have access
- Export citation
A KADISON–SAKAI-TYPE THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 249-257
-
- Article
-
- You have access
- Export citation
ON THE GOWERS NORM OF PSEUDORANDOM BINARY SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 259-271
-
- Article
-
- You have access
- Export citation
THE GENUS OF PERIODIC LINKS WITH RATIONAL QUOTIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 273-284
-
- Article
-
- You have access
- Export citation
THE DIRICHLET PROBLEM FOR BAIRE-TWO FUNCTIONS ON SIMPLICES
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2009, pp. 285-297
-
- Article
-
- You have access
- Export citation
COMMON FACTORS OF RESULTANTS MODULO p
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 299-302
-
- Article
-
- You have access
- Export citation
EMBEDDING GROUPS OF CLASS TWO AND PRIME EXPONENT IN CAPABLE AND NONCAPABLE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 303-308
-
- Article
-
- You have access
- Export citation
FRÉCHET INTERMEDIATE DIFFERENTIABILITY OF LIPSCHITZ FUNCTIONS ON ASPLUND SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 309-317
-
- Article
-
- You have access
- Export citation
ESSENTIAL AMENABILITY OF ABSTRACT SEGAL ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 319-325
-
- Article
-
- You have access
- Export citation
INJECTIVE TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 327-336
-
- Article
-
- You have access
- Export citation
ON MOROZOV’S DISCREPANCY PRINCIPLE FOR NONLINEAR ILL-POSED EQUATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 337-342
-
- Article
-
- You have access
- Export citation
GROUPS WITH COMMUTING POWERS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2009, pp. 343-351
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
BAZ volume 79 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
BAZ volume 79 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation


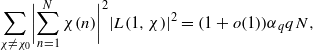
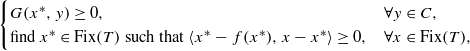
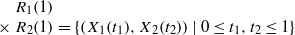 . The result of Hu generalizes [Some fractal sets determined by stable processes,
. The result of Hu generalizes [Some fractal sets determined by stable processes, 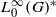 for a locally compact group
for a locally compact group 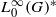 , and prove that the existence of a compact left multiplier on
, and prove that the existence of a compact left multiplier on 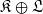 and
and 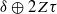 , where
, where 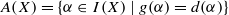 . For example, we describe Green’s relations and ideals in
. For example, we describe Green’s relations and ideals in