Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-30T17:51:40.628Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SOME WEIGHTED AVERAGE VALUES OF L-FUNCTIONS

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  26 February 2009

IGOR E. SHPARLINSKI
IGOR E. SHPARLINSKI*
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let q≥2 and N≥1 be integers. W. Zhang recently proved that for any fixed ε>0 and qε≤N≤q1/2−ε, 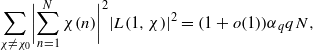where the sum is taken over all nonprincipal characters χ modulo q, L(1,χ) denotes the L-functions corresponding to χ, and αq=qo(1) is some explicit function of q. Here we improve this result and show that the same asymptotic formula holds in the essentially full range qε≤N≤q1−ε.

Keywords

L-functioncharacter sumaverage value

MSC classification

Secondary: 11M06: $zeta (s)$ and $L(s, chi)$
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 79 , Issue 2 , April 2009 , pp. 183 - 186
Copyright
Copyright © Australian Mathematical Society 2009

Footnotes

During the preparation of this work, the author was supported in part by ARC Grant DP0556431.

References

[1] Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers (Oxford University Press, Oxford, 1979).Google Scholar
[2] Zhang, W., ‘On the mean value of L-functions with the weight of character sums’, J. Number Theory 128 (2008), 2459–2466.CrossRefGoogle Scholar