Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
NASR-ISFAHANI, RASOUL
and
NEMATI, MEHDI
2011.
ESSENTIAL CHARACTER AMENABILITY OF BANACH ALGEBRAS.
Bulletin of the Australian Mathematical Society,
Vol. 84,
Issue. 3,
p.
372.
Maghsoudi, Saeid
and
Nasr-Isfahani, Rasoul
2012.
On the Maximal and Minimal Left Ideals of Certain Banach Algebras on Locally Compact Groups.
Results in Mathematics,
Vol. 62,
Issue. 1-2,
p.
157.
JAVANSHIRI, HOSSEIN
and
NASR-ISFAHANI, RASOUL
2013.
THE STRONG DUAL OF MEASURE ALGEBRAS WITH CERTAIN LOCALLY CONVEX TOPOLOGIES.
Bulletin of the Australian Mathematical Society,
Vol. 87,
Issue. 3,
p.
353.
Akhtari, Fatemeh
and
Nasr-Isfahani, Rasoul
2014.
Involutions on certain Banach algebras related to locally compact groups.
Periodica Mathematica Hungarica,
Vol. 68,
Issue. 2,
p.
143.
Mehdipour, Mohammad Javad
and
Saeedi, Zahra
2016.
Derivations on group algebras of a locally compact abelian group.
Monatshefte für Mathematik,
Vol. 180,
Issue. 3,
p.
595.
Chen, Lin
Mehdipour, Mohammad Javad
and
Li, Jun
2024.
σ-symmetric amenability of Banach algebras.
Georgian Mathematical Journal,
Vol. 31,
Issue. 6,
p.
933.


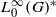 for a locally compact group
for a locally compact group 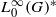 , and prove that the existence of a compact left multiplier on
, and prove that the existence of a compact left multiplier on 