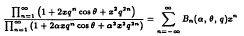Research Article
Calculus rules for combinations of ellipsoids and applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-12
-
- Article
-
- You have access
- Export citation
On Hermite-Fejér type interpolation on the Chebyshev nodes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 13-24
-
- Article
-
- You have access
- Export citation
On minimax inequalities on spaces having certain contractible subsets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 25-40
-
- Article
-
- You have access
- Export citation
Periods for triangular maps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 41-53
-
- Article
-
- You have access
- Export citation
On the signature of generalised Seifert fibrations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 55-58
-
- Article
-
- You have access
- Export citation
Posets of ordered compactifications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 59-72
-
- Article
-
- You have access
- Export citation
A direct ellipsoid method for linear programming
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 73-78
-
- Article
-
- You have access
- Export citation
Posets, near unanimity functions and zigzags
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 79-93
-
- Article
-
- You have access
- Export citation
Projectivity and duality in a Morita context
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 95-100
-
- Article
-
- You have access
- Export citation
Critical point theorems with relaxed boundary condition and applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-118
-
- Article
-
- You have access
- Export citation
Ultrabornological Bochner integrable function spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 119-126
-
- Article
-
- You have access
- Export citation
Eigenvalue estimates and isoperimetric inequalities for cone-manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 127-143
-
- Article
-
- You have access
- Export citation
Embedding up to homotopy type in Euclidean space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-148
-
- Article
-
- You have access
- Export citation
The natural topology of Matlis reflexive modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 149-154
-
- Article
-
- You have access
- Export citation
Ramanujan's remarkable summation formula and an interesting convolution identity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 155-162
-
- Article
-
- You have access
- Export citation
Power roots of polynomials
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 163-168
-
- Article
-
- You have access
- Export citation
The structure of certain group C*-algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-174
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Compact quantum systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 175-176
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 47 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 47 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation