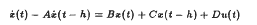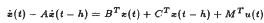Research Article
Sur les cones (faiblement complets) contenus dans le dual d'un espace de Banach non-reflexif
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-328
-
- Article
-
- You have access
- Export citation
Properties of axial diameters
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-333
-
- Article
-
- You have access
- Export citation
On convergence of the conjugate Fourier series of a function of Wiener's class
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 335-338
-
- Article
-
- You have access
- Export citation
Morita duality and artinian left duo rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 339-342
-
- Article
-
- You have access
- Export citation
Subdirect decompositions of the lattice of varieties of completely regular semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 343-351
-
- Article
-
- You have access
- Export citation
Weakly compact operators and the strict topologies
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-359
-
- Article
-
- You have access
- Export citation
Deformations of rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 361-367
-
- Article
-
- You have access
- Export citation
Uniformisation of the twice–punctured disc - problems of confluence
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-387
-
- Article
-
- You have access
- Export citation
The bisection width of cubic graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 389-396
-
- Article
-
- You have access
- Export citation
Property preserving operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 397-404
-
- Article
-
- You have access
- Export citation
Besov-type characterisations for the Bloch space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 405-420
-
- Article
-
- You have access
- Export citation
Idempotents in bicategories
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-434
-
- Article
-
- You have access
- Export citation
On the area growth of a hyperbolic surface
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 435-438
-
- Article
-
- You have access
- Export citation
Local boundedness of monotone operators under minimal hypotheses
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 439-441
-
- Article
-
- You have access
- Export citation
On the twice differentiability of viscosity solutions of nonlinear elliptic equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 443-447
-
- Article
-
- You have access
- Export citation
Compactness and convexity of cores of targets for neutral systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 449-459
-
- Article
-
- You have access
- Export citation
Inequalities and semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 461-469
-
- Article
-
- You have access
- Export citation
On the superpostition of functions in carleman classes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 471-476
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Extrapolation methods and iterative computation of derivatives of eigensystems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-478
-
- Article
-
- You have access
- Export citation
Corrigendum
Strongly Right Fbn Rings: Corrigendum
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 479
-
- Article
-
- You have access
- Export citation

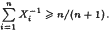 .
. for every
for every 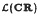 of the title then the map given by
of the title then the map given by 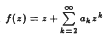 that are analytic and univalent in |
that are analytic and univalent in |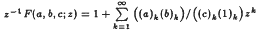 is a hypergeometric Gauss function with (
is a hypergeometric Gauss function with (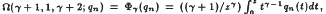 , is univalent in |
, is univalent in | . Finally we discuss the related spaces
. Finally we discuss the related spaces