Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-27T02:47:38.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactness and convexity of cores of targets for neutral systems

Published online by Cambridge University Press:  17 April 2009

Anthony N. Eke
Anthony N. Eke
Affiliation:
Department of Mathematics, University of Nigeria, Nsukka, Nigeria.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove the convexity and the compactness of the cores of targets for neutral control systems. We make use of a weak compactness argument; but in the crucial part where we establish the boundeduess of the cores of the target we make use of the notion of asymptotic direction from convex Set Theory. Let En be n-dimensional Euclidean space. We prove that the core of the target H = L + E (where L = {x ∈ En | Mx = 0}, M is a constant in m × n matrix and E is a compact, convex set containing 0) of the neutral system

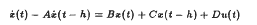
is convex, and is compact if, and only if, the system

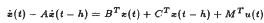
is Euclidean controllable.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 39 , Issue 3 , June 1989 , pp. 449 - 459
Copyright
Copyright © Australian Mathematical Society 1989

References

[1] Chukwu, E.N. and Silliman, S.D., ‘Constrained controllability to a closed target set’, J. Optim. Theory Appl. 21 (1978), 369–383.CrossRefGoogle Scholar
[2] Driver, R.D., Ordinary and Delay Differential Equations, Appl. Math. Sci., vol 20 (Springer-Verlag, Berlin, Heidelberg, New York, 1976).Google Scholar
[3] Dunford, M. and Schwartz, J.T., Linear Operators, Part I (John Wiley and Sons, Interscience, New York, 1958).Google Scholar
[4] Hajek, O., ‘Cores of targets in linear control systems’, Math. Systems Theory 8 (1974), 203–206.CrossRefGoogle Scholar
[5] Hale, Jack, Theory of Functional Differential Equations, Appl. Math. Sci., vol 3 (Springer-Verlag, Berlin, Heidlleberg, New York, 1977).CrossRefGoogle Scholar