Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Scott, Paul R.
1991.
Volume inequalities using sections of convex sets.
Bulletin of the Australian Mathematical Society,
Vol. 43,
Issue. 3,
p.
393.
Lassak, Marek
2001.
Relationships between widths of a convex body and of an inscribed parallelotope.
Bulletin of the Australian Mathematical Society,
Vol. 63,
Issue. 1,
p.
133.
Nevskii, M. V.
2010.
On a property of n-dimensional simplices.
Mathematical Notes,
Vol. 87,
Issue. 3-4,
p.
543.
Невский, Михаил Викторович
and
Nevskij, Mikhail Viktorovich
2010.
Об одном свойстве $n$-мерного симплекса.
Математические заметки,
Vol. 87,
Issue. 4,
p.
580.
Nevskii, Mikhail
2011.
Properties of Axial Diameters of a Simplex.
Discrete & Computational Geometry,
Vol. 46,
Issue. 2,
p.
301.
Невский, Михаил Викторович
and
Nevskij, Mikhail Viktorovich
2011.
Об осевых диаметрах выпуклого тела.
Математические заметки,
Vol. 90,
Issue. 2,
p.
313.
Nevskii, M. V.
2011.
On the axial diameters of a convex body.
Mathematical Notes,
Vol. 90,
Issue. 1-2,
p.
295.
Nevskii, M. V.
2013.
On the minimal positive homothetic image of a simplex containing a convex body.
Mathematical Notes,
Vol. 93,
Issue. 3-4,
p.
470.
Невский
and
Nevskij
2013.
О минимальном положительном гомотетическом образе симплекса, содержащем выпуклое тело.
Математические заметки,
Vol. 93,
Issue. 3,
p.
448.
Nevskii, M. V.
2014.
On one problem for a simplex and a cube in ℝ n.
Automatic Control and Computer Sciences,
Vol. 48,
Issue. 7,
p.
521.
Nevskii, M. V.
2014.
Computation of the Longest Segment of a Given Direction in a Simplex.
Journal of Mathematical Sciences,
Vol. 203,
Issue. 6,
p.
851.
Nevskii, M. V.
2015.
On Some Results in the Geometry of Convex Bodies and their Applications.
Modeling and Analysis of Information Systems,
Vol. 19,
Issue. 3,
p.
113.
Nevskii, M. V.
and
Ukhalov, A. Yu.
2017.
On Numerical Characteristics of a Simplex and Their Estimates.
Automatic Control and Computer Sciences,
Vol. 51,
Issue. 7,
p.
757.
Nevskii, M. V.
and
Ukhalov, A. Yu.
2017.
New Estimates of Numerical Values Related to a Simplex.
Automatic Control and Computer Sciences,
Vol. 51,
Issue. 7,
p.
770.
Nevskii, M. V.
and
Ukhalov, A. Yu.
2018.
On Optimal Interpolation by Linear Functions on n-Dimensional Cube.
Automatic Control and Computer Sciences,
Vol. 52,
Issue. 7,
p.
828.
Nevskii, M. V.
and
Ukhalov, A. Yu.
2018.
On Minimal Absorption Index for an n-Dimensional Simplex.
Automatic Control and Computer Sciences,
Vol. 52,
Issue. 7,
p.
680.
Nevskii, Mikhail
and
Ukhalov, Alexey
2018.
Perfect simplices in
$${\mathbb R}^5$$
R
5
.
Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry,
Vol. 59,
Issue. 3,
p.
501.
Nevskii, M. V.
and
Ukhalov, A. Yu.
2018.
On n-Dimensional Simplices Satisfying Inclusions
$$S \subset {{[0,1]}^{n}} \subset nS$$
.
Automatic Control and Computer Sciences,
Vol. 52,
Issue. 7,
p.
667.
Nevskii, M. V.
and
Ukhalov, A. Yu.
2018.
Some Properties of 0/1-Simplices.
Izvestiya of Saratov University. New Series. Series: Mathematics. Mechanics. Informatics,
Vol. 18,
Issue. 3,
p.
305.
Nevskii, Mikhail V.
and
Ukhalov, Alexey Yu.
2018.
On Optimal Interpolation by Linear Functions on an n-Dimensional Cube.
Modeling and Analysis of Information Systems,
Vol. 25,
Issue. 3,
p.
291.


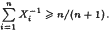 .
.