No CrossRef data available.
Article contents
Structure of the kernels associated with invariant subspaces of the Bergman shift
Published online by Cambridge University Press: 17 April 2009
Abstract
In this article we consider index 1 invariant subspaces M of the operator of multiplication by ζ(z) = z, Mζ, on the Bergman space 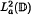 of the unit disc . It turns out that there is a positive sesquianalytic kernel lλ defined on × which determines M uniquely. Here we study the boundary behaviour and some of the basic properties of the kernel lλ. Among other things, we show that if the lower zero set of M,
of the unit disc . It turns out that there is a positive sesquianalytic kernel lλ defined on × which determines M uniquely. Here we study the boundary behaviour and some of the basic properties of the kernel lλ. Among other things, we show that if the lower zero set of M, 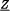 (M), is nonempty, the kernel lλ for fixed λ ∈ has a meromorphic continuation across \
(M), is nonempty, the kernel lλ for fixed λ ∈ has a meromorphic continuation across \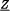 (M), where is the unit circle. Furthermore we consider some special type of kernels lλ and by studying their structure we obtain information for the invariant subspaces related to them. Lastly, and after introducing the general for the invariant subspaces related to them. Lastly, and after introducing the general vector valued setting, we discuss some analogous results for the case of
(M), where is the unit circle. Furthermore we consider some special type of kernels lλ and by studying their structure we obtain information for the invariant subspaces related to them. Lastly, and after introducing the general for the invariant subspaces related to them. Lastly, and after introducing the general vector valued setting, we discuss some analogous results for the case of 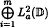 , where m is a positive integer.
, where m is a positive integer.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2003


