Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T04:41:44.636Z Has data issue: false hasContentIssue false
  • English
  • Français

A QUANTITATIVE EXTENSION OF SZLENK’S THEOREM

Part of: Special methods of summability Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  20 February 2019

ANDRZEJ KRYCZKA Open the ORCID record for ANDRZEJ KRYCZKA [Opens in a new window]
ANDRZEJ KRYCZKA*
Affiliation:
Institute of Mathematics, Maria Curie-Skłodowska University, 20-031 Lublin, Poland email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that for a bounded subset 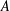$A$ of the 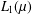$L_{1}(\unicode[STIX]{x1D707})$ space with finite measure 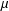$\unicode[STIX]{x1D707}$, the measure of weak noncompactness of 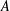$A$ based on the convex separation of sequences coincides with the measure of deviation from the Banach–Saks property expressed by the arithmetic separation of sequences. A similar result holds for a related quantity with the alternating signs Banach–Saks property. The results provide a geometric and quantitative extension of Szlenk’s theorem saying that every weakly convergent sequence in the Lebesgue space 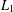$L_{1}$ has a subsequence whose arithmetic means are norm convergent.

Keywords

Cesàro summabilityBanach–Saks propertyweak compactnessLebesgue spacespreading models

MSC classification

Primary: 46B50: Compactness in Banach (or normed) spaces
Secondary: 40G05: Cesàro, Euler, Nörlund and Hausdorff methods
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 338 - 343
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Appell, J. and De Pascale, E., ‘Su alcuni parametri connessi con la misura di non compattezza di Hausdorff in spazi di funzioni misurabili’, Boll. Un. Mat. Ital. B 3 (1984), 497–515.Google Scholar
Baernstein II, A., ‘On reflexivity and summability’, Studia Math. 42 (1972), 91–94.10.4064/sm-42-1-91-94Google Scholar
Banach, S. and Saks, S., ‘Sur la convergence forte dans les champs L p ’, Studia Math. 2 (1930), 51–57.10.4064/sm-2-1-51-57Google Scholar
Banaś, J. and Martinón, A., ‘Measures of weak noncompactness in Banach sequence spaces’, Portugal. Math. 52 (1995), 131–138.Google Scholar
Beauzamy, B., ‘Banach–Saks properties and spreading models’, Math. Scand. 44 (1979), 357–384.10.7146/math.scand.a-11818Google Scholar
Beauzamy, B. and Lapresté, J.-T., Modèles étalés des espaces de Banach (Hermann, Paris, 1984).Google Scholar
Bendová, H., Kalenda, O. F. K. and Spurný, J., ‘Quantification of the Banach–Saks property’, J. Funct. Anal. 268 (2015), 1733–1754.10.1016/j.jfa.2014.12.003Google Scholar
Brunel, A. and Sucheston, L., ‘On B-convex Banach spaces’, Math. Systems Theory 7 (1974), 294–299.10.1007/BF01795947Google Scholar
De Blasi, F. S., ‘On a property of the unit sphere in a Banach space’, Bull. Math. Soc. Sci. Math. Roumanie S. Roumanie (N.S.) 21(69) (1977), 259–262.Google Scholar
Diestel, J., Geometry of Banach Spaces—Selected Topics (Springer, Berlin–New York, 1975).Google Scholar
Fabian, M., Hájek, P., Montesinos, V. and Zizler, V., ‘A quantitative version of Krein’s theorem’, Rev. Mat. Iberoam. 21 (2005), 237–248.10.4171/RMI/421Google Scholar
James, R. C., ‘Weak compactness and reflexivity’, Israel J. Math. 2 (1964), 101–119.Google Scholar
Kryczka, A., ‘Arithmetic separation and Banach–Saks sets’, J. Math. Anal. Appl. 394 (2012), 772–780.Google Scholar
Kryczka, A. and Prus, S., ‘Measure of weak noncompactness under complex interpolation’, Studia Math. 147 (2001), 89–102.10.4064/sm147-1-7Google Scholar
Kryczka, A., Prus, S. and Szczepanik, M., ‘Measure of weak noncompactness and real interpolation of operators’, Bull. Aust. Math. Soc. 62 (2000), 389–401.Google Scholar
Nishiura, T. and Waterman, D., ‘Reflexivity and summability’, Studia Math. 23 (1963), 53–57.Google Scholar
Szlenk, W., ‘Sur les suites faiblement convergentes dans l’espace L ’, Studia Math. 25 (1965), 337–341.10.4064/sm-25-3-337-341Google Scholar