No CrossRef data available.
Article contents
Norm of a linear combination of two operators on a Hilbert space
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let α, β γ, δ be complex numbers such that γδ ≠ 0. If A and B are bounded linear operators on the Hilbert space H such that γA + δB is right invertible then we study the operator norm of (αA + βB)(γA + δB)−1 using the angle φ between two subspaces ran A and ran B or the angle ψ = ψ(A, B) between two operators A and B where
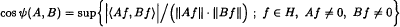
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2002
References
[1]Feldman, I.A., Krupnik, N.Ja. and Markus, A.S., ‘On the norm of two adjoint projections’, Integral Equations Operator Theory 14 (1991), 69–90.Google Scholar
[2]Gohberg, I.C. and Krein, M.G., Introduction to the theory of linear nonselfadjoint operators (Amer. Math. Soc., Providence, R.I., 1969).Google Scholar
[3]Gohberg, I.C. and Krupnik, N.Ja., One-dimensional linear singular integral equations I, II (Birkhäuser Verlag, Basel, 1992).Google Scholar
[4]Helson, H. and Szegő, G., ‘A problem in prediction theory’, Ann. Mat. Pura Appl. 51 (1960), 107–138.Google Scholar
[5]Nakazi, T., ‘Two dimensional Q-algebras’, Linear Algebra Appl. 315 (2000), 197–205.Google Scholar
[6]Spitkovsky, I.M., ‘Some estimates for the partial indices of measurable matrix-valued functions’, Math. USSR-Sb. 39 (1981), 207–226.Google Scholar


