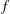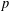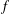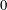Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aroca, Fuensanta
and
Rond, Guillaume
2019.
Support of Laurent series algebraic over the field of formal power series.
Proceedings of the London Mathematical Society,
Vol. 118,
Issue. 3,
p.
577.