Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Silverman, Herb
1991.
A Survey with Open Problems on Univalent Functions Whose Coefficients are Negative.
Rocky Mountain Journal of Mathematics,
Vol. 21,
Issue. 3,


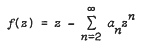 be analytic in the unit disc
be analytic in the unit disc 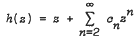 with
with 