Research Article
Cyclability of r-regular r-connected graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-11
-
- Article
-
- You have access
- Export citation
Sharp estimates of approximation by some positive linear operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 13-18
-
- Article
-
- You have access
- Export citation
A translation plane of order 81 and its full collineation group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 19-34
-
- Article
-
- You have access
- Export citation
P-groups with non-abelian automorphism groups and all automorphisms central
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 35-37
-
- Article
-
- You have access
- Export citation
On the Möbius function of Hom(P, Q)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 39-46
-
- Article
-
- You have access
- Export citation
Countable sum theorem for locally closed sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 47-55
-
- Article
-
- You have access
- Export citation
Existence of solutions of Oseen type integral equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 57-66
-
- Article
-
- You have access
- Export citation
Small subharmonic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 67-82
-
- Article
-
- You have access
- Export citation
Analytic mappings with negative coefficients in the unit disc
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-91
-
- Article
-
- You have access
- Export citation
Stability of functional differential equations of Volterra type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 93-100
-
- Article
-
- You have access
- Export citation
Conference in Honour of Kurt Mahler
Some suggestions for further research
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-108
-
- Article
-
- You have access
- Export citation
p-adic methods in the study of Taylor coefficients of rational functions*
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 109-117
-
- Article
-
- You have access
- Export citation
The n-dimensional approximation constatant*
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 119-125
-
- Article
-
- You have access
- Export citation
A method of Mahler in transcendence theory and some of its applications*
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 127-136
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
A Unified Theory of Causal Models
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-138
-
- Article
-
- You have access
- Export citation
Discrete Green's functions and random resistive networks
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 139-140
-
- Article
-
- You have access
- Export citation
Optimization in abstract spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 141-143
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 29 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 29 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

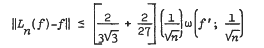
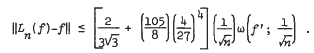
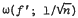 ) our result cannot be sharpened further by taking higher order moments.
) our result cannot be sharpened further by taking higher order moments.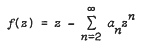 be analytic in the unit disc
be analytic in the unit disc 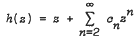 with
with