Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T00:54:08.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Interpretability in Robinson's Q

Published online by Cambridge University Press:  05 September 2014

Fernando Ferreira  and
Gilda Ferreira
Fernando Ferreira
Affiliation:
Universidade de Lisboa, Faculdade de Ci'encias, Departamento de Matemática, Campo Grande, ED. C6 1749-016 Lisboa, Portugal E-mail: [email protected] Universidade Lusófona de Humanidades e Tecnologias, Departamento de Matemática, AV. Do Campo Grande 376, 1749-024 Lisboa, Portugal
Gilda Ferreira
Affiliation:
Universidade de Lisboa, Faculdade de Ciências, Departamento de Matemática, Campo Grande, ED. C6, 1749-016 Lisboa, Portugal E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Edward Nelson published in 1986 a book defending an extreme formalist view of mathematics according to which there is an impassable barrier in the totality of exponentiation. On the positive side, Nelson embarks on a program of investigating how much mathematics can be interpreted in Raphael Robinson's theory of arithmetic 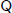. In the shadow of this program, some very nice logical investigations and results were produced by a number of people, not only regarding what can be interpreted in 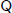but also what cannot be so interpreted. We explain some of these results and rely on them to discuss Nelson's position.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 19 , Issue 3 , September 2013 , pp. 289 - 317
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Barwise, J., Admissible set theory and structures: An approach to definability theory, Perspectives in Mathematical Logic, Springer, 1975.CrossRefGoogle Scholar
[2] Bellantoni, S. and Cook, S., A new recursion-theoretic characterization of the polytime functions, Computational Complexity, vol. 2 (1992), pp. 97–110.CrossRefGoogle Scholar
[3] Bennett, J., On spectra, Ph.D. thesis, Princeton University, Princeton, New Jersey, 1962.Google Scholar
[4] Burgess, J. and Hazen, A., Predicative logic and formal arithmetic, Notre Dame Journal of Formal Logic, vol. 39 (1998), pp. 1–17.CrossRefGoogle Scholar
[5] Buss, S. R., Bounded arithmetic, Ph.D. thesis, Princeton University, 1985, a revision of this thesis was published by Bibliopolis (Naples) in 1986.Google Scholar
[6] Buss, S. R., Nelson's work on logic and foundations and other reflections on foundations of mathematics, Diffusion, quantum theory, and radically elementary mathematics (Faris, W., editor), Princeton University Press, 2006, pp. 183–208.CrossRefGoogle Scholar
[7] Cantini, A., Asymmetric interpretations for bounded theories, Mathematical Logic Quarterly, vol. 42 (1996), no. 1, pp. 270–288.CrossRefGoogle Scholar
[8] Dimitracopoulos, C., Matiyasevič theorem and fragments of arithmetic, Ph.D. thesis, University of Manchester, 1980.Google Scholar
[9] Ewald, W. (editor), From Kant to Hilbert, vol. 2, Oxford University Press, 1996.Google Scholar
[10] Feferman, S., Arithmetization of metamathematics in a general setting, Fundamenta Mathematicae, vol. 49 (1960), pp. 35–92.CrossRefGoogle Scholar
[11] Feferman, S., Systems of predicative analysis, The Journal of Symbolic Logic, vol. 29 (1964), no. 1, pp. 1–30.CrossRefGoogle Scholar
[12] Fernandes, A. M., Investigações em sistemas de análise exequível, Ph.D. thesis, Universidade de Lisboa, Portugal, 2001, (in Portuguese).Google Scholar
[13] Fernandes, A. M., A new conservation result of WKL0 over RCA0 , Archive for Mathematical Logic, vol. 41 (2002), pp. 55–63.CrossRefGoogle Scholar
[14] Fernandes, A. M., Strict Π1 1-reflection in bounded arithmetic, Archive for Mathematical Logic, vol. 49 (2010), pp. 17–34.CrossRefGoogle Scholar
[15] Fernandes, A. M. and Ferreira, F., Groundwork for weak analysis, The Journal of Symbolic Logic, vol. 67 (2002), no. 2, pp. 557–578.CrossRefGoogle Scholar
[16] Ferreira, F., Polynomial time computable arithmetic and conservative extensions, Ph.D. thesis, Pennsylvania State University, USA, 1988.Google Scholar
[17] Ferreira, F., Polynomial time computable arithmetic, Logic and computation (Sieg, W., editor), American Mathematical Society, 1990, pp. 161–180.Google Scholar
[18] Ferreira, F., A feasible theory for analysis, The Journal of Symbolic Logic, vol. 59 (1994), no. 3, pp. 1001–1011.CrossRefGoogle Scholar
[19] Ferreira, F. and Ferreira, G., The Riemann integral in weak systems of analysis, Journal of Universal Computer Science, vol. 14 (2008), no. 6, pp. 908–937.Google Scholar
[20] Ferreira, G., Aritmética computável em espaço polinomial, Master's thesis, Universidade de Lisboa, 2001, (in Portuguese).Google Scholar
[21] Ferreira, G., Sistemas de análise fraca para a integração, Ph.D. thesis, Universidade de Lisboa, 2006, (in Portuguese).Google Scholar
[22] Friedman, H., FOM: 73:Hilbert's program wide open?, FOM e-mail list: http://www.cs.nyu.edu/pipermail/fom/1999-December/003511.html, 12 20, 1999.Google Scholar
[23] Greenberg, M. J., Old and new results in the foundations of elementary plane Euclidean and non-Euclidean geometries, American Mathematical Monthly, vol. 117 (2010), no. 3, pp. 198–219.CrossRefGoogle Scholar
[24] Hájek, P., Interpretability and fragments of arithmetic, Arithmetic, proof theory and computational complexity (Clote, P. and Krajíček, J., editors), Clarendon Press, Oxford, 1993, pp. 185–196.Google Scholar
[25] Hájek, P. and Pudlák, P., Metamathematics of first-order arithmetic, Perspectives in Mathematical Logic, Springer, 1993.CrossRefGoogle Scholar
[26] Krajíček, J., Bounded arithmetic, propositional logic, and complexity theory, Encyclopedia of Mathematics and its Applications, vol. 60, Cambridge University Press, 1995.CrossRefGoogle Scholar
[27] Marker, D., Model theory: An introduction, vol. 217, Springer, 2002.Google Scholar
[28] Nelson, E., Predicative arithmetic, Mathematical Notes, Princeton University Press, 1986.CrossRefGoogle Scholar
[29] Nelson, E., Confessions of an apostate mathematician, paper available at https://web.math.princeton.edu/~nelson/papers.html, 1995.Google Scholar
[30] Nelson, E., Completed versus incomplete infinity in arithmetic, paper available at https://web.math.princeton.edu/~nelson/papers.html, 2005.Google Scholar
[31] Nelson, E., Warning signs of a possible collapse of contemporary mathematics, Infinity. New research frontiers (Heller, M. and Woodin, H., editors), Cambridge University Press, 2011, pp. 76–85.CrossRefGoogle Scholar
[32] Parsons, C., Mathematical thought and its objects, CambridgeUniversity Press, 2008.Google Scholar
[33] Poincaré, H., Les mathématiques et la logique, Revue de métaphysic et de moral, vol. 14 (1906), pp. 294–317, English translation in [9], pp. 1052–1071.Google Scholar
[34] Pudlák, P., Cuts, consistency statements and interpretations, The Journal of Symbolic Logic, vol. 50 (1985), no. 2, pp. 423–441.CrossRefGoogle Scholar
[35] Robinson, R.M., An essentially undecidable axiom system, Proceedings of the International Congress of Mathematicians, Cambridge 1950, vol. 1, American Mathematics Society, 1952, pp. 729–730.Google Scholar
[36] Sacks, G., Higher recursion theory, Perspectives in Mathematical Logic, Springer, 1990.CrossRefGoogle Scholar
[37] Schwartz, J. T., Do the integers exist? The unknowability of arithmetic consistency, Communications on Pure and Applied Mathematics, vol. 58 (2005), no. 9, pp. 1280–1286.CrossRefGoogle Scholar
[38] Simpson, S. G., Subsystems of second order arithmetic, Perspectives in Mathematical Logic, Springer, 1999.CrossRefGoogle Scholar
[39] Smoryński, C., The incompleteness theorems, Handbook of mathematical logic (Barwise, J., editor), Studies in Logic and the Foundations of Mathematics, vol. 90, North Holland, 1977, pp. 821–865.CrossRefGoogle Scholar
[40] Solovay, R.M., Letter to P. Hajék, 08 1976.Google Scholar
[41] Tarski, A., A decision method for elementary algebra and geometry, Technical report, Rand Corporation, 1957, second edition. Prepared for publication by J. C. C. McKinsey. First edition published in 1948.Google Scholar
[42] Tarski, A., Mostowski, A., and Robinson, R., Undecidable theories, North-Holland, 1953.Google Scholar
[43] Visser, A., Interpretability logic, Mathematical logic (Petkov, P. P., editor), Plenum Press, 1990, pp. 307–359.Google Scholar
[44] Visser, A., The formalization of interpretability, Studia Logica, vol. 50 (1991), no. 1, pp. 81–105.CrossRefGoogle Scholar
[45] Visser, A., The unprovability of small inconsistency, Archive for Mathematical Logic, vol. 32 (1993), no. 4, pp. 275–298.CrossRefGoogle Scholar
[46] Voevodsky, V., What if current foundations of mathematics are inconsistent?, Video lecture commemorating the 80th anniversary of the Institute for Advanced Study (Princeton), 2010, available at http://video.ias.edu/voevodsky-80th.Google Scholar
[47] Weyl, H., Das Kontinuum, Veit, Leipzig, 1918.CrossRefGoogle Scholar
[48] Wilikie, A., On sentences interpretable in systems of arithmetic, Logic colloquium 1984 (Paris, J., Wilkie, A., and Wilmers, G., editors), North Holland, 1986, pp. 329–342.Google Scholar
[49] Wilkie, A. and Paris, J., On the scheme of induction for bounded arithmetic formulas, Annals of Pure and Applide Logic, vol. 35 (1987), pp. 261–302.CrossRefGoogle Scholar
[50] Zambella, D., Notes on polynomially bounded arithmetic, The Journal of Symbolic Logic, vol. 61 (1996), pp. 942–966.CrossRefGoogle Scholar