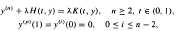Research Article
On the scattering of waves by nearly hard or soft incomplete vertical barriers in water of infinite depth
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 293-307
-
- Article
-
- You have access
- Export citation
Reflection of water waves in the presence of surface tension by a nearly vertical porous wall
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 308-317
-
- Article
-
- You have access
- Export citation
Scattering of water waves by a submerged thin vertical wall with a gap
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 318-331
-
- Article
-
- You have access
- Export citation
Bubbles rising in an inclined two-dimensional tube and jets falling along a wall
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 332-349
-
- Article
-
- You have access
- Export citation
An inequality for probability density functions arising from a distinguishability problem
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 350-354
-
- Article
-
- You have access
- Export citation
Integration of trivariate polynomials over linear polyhedra in Euclidean three-dimensional space
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 355-385
-
- Article
-
- You have access
- Export citation
Eigenvalue characterization for (n · p) boundary-value problems
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 386-407
-
- Article
-
- You have access
- Export citation
Spectral collocation methods for a partial integro-differential equation with a weakly singular kernel
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. 408-430
-
- Article
-
- You have access
- Export citation
Front matter
ANZ volume 39 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ANZ volume 39 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 February 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 the angle β between the left wall and the horizontal, and the angle γ between the free surface and the right wall at the separation point. Numerical solutions are obtained
the angle β between the left wall and the horizontal, and the angle γ between the free surface and the right wall at the separation point. Numerical solutions are obtained