Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T07:13:14.764Z Has data issue: false hasContentIssue false
  • English
  • Français

An inequality for probability density functions arising from a distinguishability problem

Published online by Cambridge University Press:  17 February 2009

Boris Guljaš ,
C. E. M. Pearce  and
Josip Pečarić
Boris Guljaš
Affiliation:
Department of Mathematics, University of Zagreb, Bijenička c. 30, 41000 Zagreb, Croatia
C. E. M. Pearce
Affiliation:
Department of Applied Mathematics, The University of Adelaide, Adelaide SA 5005, Australia
Josip Pečarić
Affiliation:
Faculty of Textile Technology, University of Zagreb, Pierottijeva 6, 41000 Zagreb, Croatia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An integral inequality is established involving a probability density function on the real line and its first two derivatives. This generalizes an earlier result of Sato and Watari. If f denotes the probability density function concerned, the inequality we prove is that

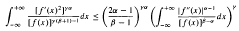
under the conditions β > α 1 and 1/(β+1) < γ ≤ 1.

Type
Research Article
Information
The ANZIAM Journal , Volume 39 , Issue 3 , January 1998 , pp. 350 - 354
Copyright
Copyright © Australian Mathematical Society 1998

References

[1] Fernique, X., “Régularité des trajectoires des fonctions aléatoires gaussiennes”, in Lecture Notes in Math. 480 (Springer-Verlag, New York, 1974), pp. 1–96.Google Scholar
[2] Kakutani, S., “On equivalence of infinite product measures”, Ann. of Math. 49 (1948) 214–224.CrossRefGoogle Scholar
[3] Kitada, K. and Sato, H., “On the absolute continuity of infinite product measure and its convolution”, Probab. Theory Related Fields 81 (1989) 609–627.CrossRefGoogle Scholar
[4] Rozanov, Yu. A., “On the density of one Gaussian measure with respect to another”, Theory Probab. Appl. 7 (1962) 82–87.CrossRefGoogle Scholar
[5] Sato, H. and Watari, C., “Some integral inequalities and absolute continuity of a symmetric random translation”, J. Functional Anal. 114 (1993) 257–266.CrossRefGoogle Scholar
[6] Shepp, L. A., “Distinguishing a sequence of random variables from a translate of itself”, Ann. Math. Statist. 36 (1965) 1107–1112.CrossRefGoogle Scholar