Research Article
Branching random walk in varying environments
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 359-367
-
- Article
- Export citation
Operator-geometric stationary distributions for markov chains, with application to queueing models
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 368-391
-
- Article
- Export citation
Storage processes with general release rule and additive inputs
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 392-433
-
- Article
- Export citation
Two suggestions of how to define a multistate coherent system
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 434-455
-
- Article
- Export citation
Front matter
APR volume 14 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
APR volume 14 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

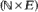 , whose transition probabilities have a particular ‘block-partitioned' structure. Examples of such chains include those studied by Neuts [8] who took
, whose transition probabilities have a particular ‘block-partitioned' structure. Examples of such chains include those studied by Neuts [8] who took 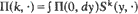 , where the operator
, where the operator 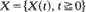 in which
in which 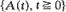 is a Lévy process with measure
is a Lévy process with measure 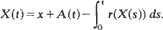
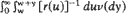 and in the case when
and in the case when