Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hajek, Bruce
1982.
Birth-and-death processes on the integers with phases and general boundaries.
Journal of Applied Probability,
Vol. 19,
Issue. 03,
p.
488.
Neuts, Marcel F.
1984.
Matrix-analytic methods in queuing theory.
European Journal of Operational Research,
Vol. 15,
Issue. 1,
p.
2.
Ramaswami, V.
and
Lucantoni, David M.
1985.
Stationary waiting time distribution in queues with phase type service and in quasi-birth-and-death processes.
Communications in Statistics. Stochastic Models,
Vol. 1,
Issue. 2,
p.
125.
Bhaskar, Sengupta
1986.
Operation research.
Communications in Statistics. Stochastic Models,
Vol. 2,
Issue. 2,
p.
251.
Sengupta, Bhaskar
1987.
Matrix geometric solutions in stochastic models.
Communications in Statistics. Stochastic Models,
Vol. 3,
Issue. 3,
p.
293.
Ramaswami, V.
1988.
Nonlinear Matrix Equations in Applied Probability—Solution Techniques and Open Problems.
SIAM Review,
Vol. 30,
Issue. 2,
p.
256.
Sengupta, Bhaskar
1989.
Markov processes whose steady state distribution is matrix-exponential with an application to theGI/PH/1 queue.
Advances in Applied Probability,
Vol. 21,
Issue. 1,
p.
159.
Sengupta, Bhaskar
1990.
The semi-markovian queue: theory and applications.
Communications in Statistics. Stochastic Models,
Vol. 6,
Issue. 3,
p.
383.
Spieksma, F.M.
and
Tweedie, R.L.
1994.
Strengthening ergodicity to geometric ergodicity for markov chains.
Communications in Statistics. Stochastic Models,
Vol. 10,
Issue. 1,
p.
45.
Yeung, Raymond W.
and
Sengupta, Bhaskar
1994.
Matrix product-form solutions for Markov chains with a tree structure.
Advances in Applied Probability,
Vol. 26,
Issue. 4,
p.
965.
Ramaswami, V.
and
Taylor, P.G.
1996.
Some properties of the rate perators in level dependent uasi-birth-and-death processes with countable number of phases.
Communications in Statistics. Stochastic Models,
Vol. 12,
Issue. 1,
p.
143.
Gass, Saul I.
and
Harris, Carl M.
1996.
Encyclopedia of Operations Research and Management Science.
p.
359.
Friis Nielsen, Bo
and
Ramaswami, V.
1997.
Teletraffic Contributions for the Information Age, Proceedings of the 15th International Teletraffic Congress - ITC 15.
Vol. 2,
Issue. ,
p.
477.
Foss, S.G.
and
Tweedie, R.L.
1998.
Perfect simulation and backward coupling∗.
Communications in Statistics. Stochastic Models,
Vol. 14,
Issue. 1-2,
p.
187.
Akar, Nail
Oğuz, Nihat C.
and
Sohraby, Khosrow
2000.
A novel computational method for solving finite qbd processes.
Communications in Statistics. Stochastic Models,
Vol. 16,
Issue. 2,
p.
273.
Neuts, Marcel F.
2001.
Encyclopedia of Operations Research and Management Science.
p.
499.
Alfa, Attahiru Sule
2002.
Discrete time queues and matrix-analytic methods.
Top,
Vol. 10,
Issue. 2,
p.
147.
Dunsmuir, William T. M.
Meyn, Sean P.
and
Roberts, Gareth
2002.
Obituary: Richard Lewis Tweedie.
Journal of Applied Probability,
Vol. 39,
Issue. 02,
p.
441.
Sapna Isotupa, K. P.
and
Stanford, David A.
2002.
AN INFINITE-PHASE QUASI-BIRTH-AND-DEATH MODEL FOR THE NON-PREEMPTIVE PRIORITYM/PH/1 QUEUE.
Stochastic Models,
Vol. 18,
Issue. 3,
p.
387.
Dunsmuir, William T. M.
Meyn, Sean P.
and
Roberts, Gareth
2002.
Obituary: Richard Lewis Tweedie.
Journal of Applied Probability,
Vol. 39,
Issue. 2,
p.
441.
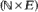 , whose transition probabilities have a particular ‘block-partitioned' structure. Examples of such chains include those studied by Neuts [8] who took E to be finite; they also include chains studied in queueing theory, such as (Nn, Sn) where Nn is the number of customers in a GI/G/1 queue immediately before, and Sn the remaining service time immediately after, the nth arrival.
, whose transition probabilities have a particular ‘block-partitioned' structure. Examples of such chains include those studied by Neuts [8] who took E to be finite; they also include chains studied in queueing theory, such as (Nn, Sn) where Nn is the number of customers in a GI/G/1 queue immediately before, and Sn the remaining service time immediately after, the nth arrival.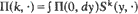 , where the operator S is the minimal solution of a non-linear operator equation. Necessary and sufficient conditions for Πto exist are also found. In the case of the GI/G/1 queueing chain above these are exactly the usual stability conditions.
, where the operator S is the minimal solution of a non-linear operator equation. Necessary and sufficient conditions for Πto exist are also found. In the case of the GI/G/1 queueing chain above these are exactly the usual stability conditions.

