Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T19:06:28.335Z Has data issue: false hasContentIssue false
  • English
  • Français

Basic properties and prediction of max-ARMA processes

Published online by Cambridge University Press:  01 July 2016

Richard A. Davis  and
Sidney I. Resnick
Richard A. Davis*
Affiliation:
Colorado State University
Sidney I. Resnick*
Affiliation:
Cornell University
*
∗Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, USA.
∗∗Postal address: Department of Operations Research and Industrial Engineering, Upson Hall, Cornell University, Ithaca, NY 14853, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

A max-autoregressive moving average (MARMA(p, q)) process {Xt} satisfies the recursion 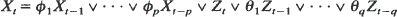for all t where φ i, 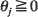, and {Zt} is i.i.d. with common distribution function Φ1,σ (X): = exp {–σ x–1} for . Such processes have finite-dimensional distributions which are max-stable and hence are examples of max-stable processes. We provide necessary and sufficient conditions for existence of a stationary solution to the MARMA recursion and we examine the reducibility of the process to a MARMA(p′, q′) with p′ <p or q′ < q. After introducing a natural metric between two jointly max-stable random variables, we consider the prediction problem for MARMA processes. Assuming that X1, …, Xn have been observed, we restrict our class of predictors to be max-linear, i.e. of the form 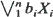, and find b1, …, bn to minimize the distance between this predictor and Xn+k for k 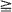1. The optimality criterion is designed to minimize the probability of large errors and is similar in spirit to the dispersion criterion adopted in Cline and Brockwell (Stoch. Proc. Appl. 19 (1985), 281-296) for the prediction of ARMA processes with stable noise. Most of our results remain valid for the case when the distribution of Z1 is only in the domain of attraction of Φ1,σ. In addition, we give a naive estimation procedure for the φ 's and the θ 's which, with probability 1, identifies the true parameter values exactly for n sufficiently large.

Keywords

MAX-STABLE DISTRIBUTIONMAX-STABLE PROCESSESPREDICTIONCAUSALITYDOMAIN OF ATTRACTION OF AN EXTREME VALUE DISTRIBUTIONARMA PROCESSES
Type
Research Article
Information
Advances in Applied Probability , Volume 21 , Issue 4 , December 1989 , pp. 781 - 803
Copyright
Copyright © Applied Probability Trust 1989 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by NSF Grant DMS-8802559, and partly carried out at the University of California, San Diego.

Research supported by NSF Grant DMS-8801034 and the Mathematical Sciences Institute at Cornell University.

References

Arnold, B. and Haslett, J. (1988) A characterization of the Pareto process among stationary stochastic processes of the form Xn = c min (Xn − 1, Yn). Preprint.Google Scholar
Balkema, A. A. and Haan, L. De (1988) Almost sure continuity of stable moving average processes with index less than one. Ann. Prob. 16, 334–343.Google Scholar
Chernick, M., Daley, D. and Littlejohn, R. (1988) A time-reversibility relationship between two Markov chains with exponential stationary distributions. J. Appl. Prob. 25, 418–422.Google Scholar
Cline, D. B. H. (1983) Estimation and Linear Prediction for Regression, Autoregression and ARMA with Infinite Variance Data. Ph.D. Dissertation, Dept. of Statistics, Colorado State University.Google Scholar
Cline, D. B. H. and Brockwell, P. J. (1985) Linear prediction of ARMA processes with infinite variance. Stoch. Proc. Appl. 19, 281–296.Google Scholar
Daley, D. and Haslett, J. (1982) A thermal energy storage process with controlled input. Adv. Appl. Prob. 14, 257–271.Google Scholar
Davis, R. A. and Mccormick, W. P. (1989) Estimation for first-order autoregressive processes with positive or bounded innovations. Stoch. Proc. Appl. 31, 237–250.Google Scholar
Fama, E. (1965) Behavior of stock market prices. J. Business, U. Chicago 38, 34–105.Google Scholar
Gade, H. (1973) Deep water exchanges in a sill fjord: a stochastic process. J. Phys. Oceanography 3, 213–219.Google Scholar
Haan, E. De (1984) A spectral representation of max-stable processes. Ann. Prob. 12, 1194–1204.Google Scholar
Haan, E. De (1985) Extremes in higher dimensions: the model and some statistics. Proc. 45th Session ISI 4, Amsterdam, 23.3, 1–15.Google Scholar
Haan, L. De (1986) A stochastic process that is autoregressive in two directions of time. Statist. Neerlandica 40, 39–45.Google Scholar
Haan, L. De and Pickands, J. (1986) Stationary min-stable stochastic processes. Prob. Theory Rel. Fields 72, 477–492.Google Scholar
Helland, I. and Nilsen, T. (1976). On a general random exchange model. J. Appl. Prob. 13, 781–790.Google Scholar
Hsing, T. (1986) Extreme value theory for the supremum of rv's with regularly varying tail probabilities. Stoch. Proc. Appl. 22, 51–57.Google Scholar
Resnick, S. (1987) Extreme Values, Regular Variation and Point Processes. Springer-Verlag, New York.Google Scholar
Stuck, B. W. and Kleiner, B. (1974) A statistical analysis of telephone noise. Bell System Tech. J. 53, 1263–1320.Google Scholar
Tiago De Oliveira, J. (1962/63) Structure theory of bivariate extremes: Extensions. Estudos de Math. Estat. Econom. 7, 165–195.Google Scholar
Yeh, H., Arnold, B. and Robertson, C. (1988) Pareto processes. J. Appl. Prob. 25, 291–301.Google Scholar