Article contents
Basic properties and prediction of max-ARMA processes
Published online by Cambridge University Press: 01 July 2016
Abstract
A max-autoregressive moving average (MARMA(p, q)) process {Xt} satisfies the recursion
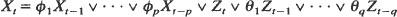 for all t where φ i,
for all t where φ i, 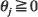 , and {Zt} is i.i.d. with common distribution function Φ1,σ (X): = exp {–σ x–1} for
, and {Zt} is i.i.d. with common distribution function Φ1,σ (X): = exp {–σ x–1} for  . Such processes have finite-dimensional distributions which are max-stable and hence are examples of max-stable processes. We provide necessary and sufficient conditions for existence of a stationary solution to the MARMA recursion and we examine the reducibility of the process to a MARMA(p′, q′) with p′ <p or q′ < q. After introducing a natural metric between two jointly max-stable random variables, we consider the prediction problem for MARMA processes. Assuming that X1, …, Xn have been observed, we restrict our class of predictors to be max-linear, i.e. of the form
. Such processes have finite-dimensional distributions which are max-stable and hence are examples of max-stable processes. We provide necessary and sufficient conditions for existence of a stationary solution to the MARMA recursion and we examine the reducibility of the process to a MARMA(p′, q′) with p′ <p or q′ < q. After introducing a natural metric between two jointly max-stable random variables, we consider the prediction problem for MARMA processes. Assuming that X1, …, Xn have been observed, we restrict our class of predictors to be max-linear, i.e. of the form 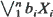 , and find b1, …, bn to minimize the distance between this predictor and Xn+k for k
, and find b1, …, bn to minimize the distance between this predictor and Xn+k for k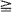 1. The optimality criterion is designed to minimize the probability of large errors and is similar in spirit to the dispersion criterion adopted in Cline and Brockwell (Stoch. Proc. Appl. 19 (1985), 281-296) for the prediction of ARMA processes with stable noise. Most of our results remain valid for the case when the distribution of Z1 is only in the domain of attraction of Φ1,σ. In addition, we give a naive estimation procedure for the φ 's and the θ 's which, with probability 1, identifies the true parameter values exactly for n sufficiently large.
1. The optimality criterion is designed to minimize the probability of large errors and is similar in spirit to the dispersion criterion adopted in Cline and Brockwell (Stoch. Proc. Appl. 19 (1985), 281-296) for the prediction of ARMA processes with stable noise. Most of our results remain valid for the case when the distribution of Z1 is only in the domain of attraction of Φ1,σ. In addition, we give a naive estimation procedure for the φ 's and the θ 's which, with probability 1, identifies the true parameter values exactly for n sufficiently large.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Applied Probability Trust 1989
Footnotes
Research supported by NSF Grant DMS-8802559, and partly carried out at the University of California, San Diego.
Research supported by NSF Grant DMS-8801034 and the Mathematical Sciences Institute at Cornell University.
References
- 81
- Cited by


