3.1 Introduction
Experiments of all kinds have once again become popular in the social sciences (Reference Druckman, Green, Kuklinski and LupiaDruckman et al. 2011). Of course, psychology has long used them. But in my own field of political science, and in adjacent areas such as economics, far more experiments are conducted now than in the twentieth century (Reference JamisonJamison 2019). Lab experiments, survey experiments, field experiments – all have become popular (for example, Reference Karpowitz and MendelbergKarpowitz and Mendelberg 2014; Reference MutzMutz 2011; and Reference Gerber and GreenGerber and Green 2012, respectively; Reference AchenAchen 2018 gives an historical overview).
In political science, much attention, both academic and popular, has been focused on field experiments, especially those studying how to get citizens to the polls on election days. Candidates and political parties care passionately about increasing the turnout of their voters, but it was not until the early twenty-first century that political campaigns became more focused on testing what works. In recent years, scholars have mounted many field experiments on turnout, often with support from the campaigns themselves. The experiments have been aimed particularly at learning the impact on registration or turnout of various kinds of notifications to voters that an election was at hand. (Reference Green, McGrath and AronowGreen, McGrath, and Aronow 2013 reviews the extensive literature.)
Researchers doing randomized experiments of all kinds have not been slow to tout the scientific rigor of their approach. They have produced formal statistical models showing that an RCT is typically vastly superior to an observational (nonrandomized) study. In statistical textbooks, of course, experimental randomization has long been treated as the gold standard for inference, and that view has become commonplace in the social sciences. More recently, however, critics have begun to question this received wisdom. Reference CartwrightCartwright (2007a, Reference Cartwright, Chao and Reiss2017, Chapter 2 this volume) and her collaborators (Reference Cartwright and HardieCartwright and Hardie 2012) have argued that RCTs have important limitations as an inferential tool. Along with Reference Heckman and SmithHeckman and Smith (1995), Reference DeatonDeaton (2010) and others, she has made it clear what experiments can and cannot hope to do.
So where did previous arguments for RCTs go wrong? In this short chapter, I take up a prominent formal argument for the superiority of experiments in political science (Reference Gerber, Green, Kaplan and TeeleGerber et al. 2014). Then, building on the work of Reference Stokes and TeeleStokes (2014), I show that the argument for experiments depends critically on emphasizing the central challenge of observational work – accounting for unobserved confounders – while ignoring entirely the central challenge of experimentation – achieving external validity. Once that imbalance is corrected, the mathematics of the model leads to a conclusion much closer to the position of Cartwright and others in her camp.
3.2 The Gerber–Green–Kaplan Model
Reference Gerber, Green, Kaplan and TeeleGerber, Green, and Kaplan (2014) make a case for the generic superiority of experiments, particularly field experiments, over observational research. To support their argument, they construct a straightforward model of Bayesian inference in the simplest case: learning the mean of a normal (Gaussian) distribution. This mean might be interpreted as an average treatment effect across the population of interest if everyone were treated, with heterogeneous treatment effects distributed normally. Thus, denoting the treatment-effects random variable by Xt and the population variance of the treatment effects by
![]() , we have the first assumption:
, we have the first assumption:
Gerber et al. implicitly take
![]() to be known; we follow them here.2
to be known; we follow them here.2
In Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014)’s setup, there are two ways to learn about µ. The first is via an RCT, such as a field experiment. They take the view that estimation of population parameters by means of random sampling is analogous to the estimation of treatment effects by means of randomized experimentation (Reference Gerber, Green, Kaplan and TeeleGerber et al. 2014, 32 at fn. 8). That is, correctly conducted experiments are always unbiased estimates of the population parameter.
Following Gerber et al.’s mathematics but making the experimental details a bit more concrete, suppose that the experiment has a treatment and a control group, each of size n, with individual outcomes distributed normally and independently:
![]() in the experimental group and
in the experimental group and
![]() in the control group. That is, the mathematical expectation of outcomes in the treatment group is the treatment effect µ, while the expected effect in the control group is 0. We assume that the sampling variance is the same in each group and that this variance is known. Let the sample means of the experimental and control groups be
in the control group. That is, the mathematical expectation of outcomes in the treatment group is the treatment effect µ, while the expected effect in the control group is 0. We assume that the sampling variance is the same in each group and that this variance is known. Let the sample means of the experimental and control groups be
![]() and
and
![]() respectively, and let their difference be
respectively, and let their difference be
![]() .
.
Then, by the textbook logic of pure experiments plus familiar results in elementary statistics, the difference
![]() is distributed as:
is distributed as:
which is unbiased for the treatment effect µ. Thus, we may define a first estimate of the treatment effect by
![]() : It is the estimate of the treatment effect coming from the experiment. This is the same result as in Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 12), except that we have spelled out here the dependence of the variance on the sample size.
: It is the estimate of the treatment effect coming from the experiment. This is the same result as in Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 12), except that we have spelled out here the dependence of the variance on the sample size.
Next, Gerber et al. assume that there is a second source of knowledge about µ, this time from an observational study with m independent observations, also independent of the experimental observations. Via regression or other statistical methods, this study generates a normally distributed estimate of the treatment effect µ, with known sampling variance
![]() . However, because the methodology is not experimental, Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 12–13) assume that the effect is estimated with confounding, so that its expected value is distorted by a bias term β. Hence, the estimate from the observational study
. However, because the methodology is not experimental, Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 12–13) assume that the effect is estimated with confounding, so that its expected value is distorted by a bias term β. Hence, the estimate from the observational study
![]() is distributed as:
is distributed as:
We now have two estimates,
![]() and
and
![]() , and we want to know how to combine them. One can proceed by constructing a minimum-mean-squared error estimate in a classical framework, or one can use Bayesian methods. Since both approaches give the same result in our setup and since the Bayesian logic is more familiar, we follow Gerber et al. in adopting it. In that case, we need prior distributions for each of the unknowns.
, and we want to know how to combine them. One can proceed by constructing a minimum-mean-squared error estimate in a classical framework, or one can use Bayesian methods. Since both approaches give the same result in our setup and since the Bayesian logic is more familiar, we follow Gerber et al. in adopting it. In that case, we need prior distributions for each of the unknowns.
With all the variances assumed known, there are just two unknown parameters, µ and β. An informative prior on µ is not ordinarily adopted in empirical research. At the extreme, as Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 15) note, a fully informative prior for µ would mean that we already knew the correct answer for certain and we would not care about either empirical study, and certainly not about comparing them. Since our interest is in precisely that comparison, we want the data to speak for themselves. Hence, we set the prior variance on µ to be wholly uninformative; in the usual Bayesian way we approximate its variance by infinity.Footnote 1
The parameter β also needs a prior. Sometimes we know the likely size and direction of bias in an observational study, and in that case we would correct the observational estimate by subtracting the expected size of the bias, as Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 14) do. For simplicity here, and because it makes no difference to the argument, we will assume that the direction of the bias is unknown and has prior mean zero, so that subtracting its mean has no effect. Then the prior distribution is:
Here
![]() represents our uncertainty about the size of the observational bias. Larger values indicate more uncertainty. Standard Bayesian logic then shows that our posterior distribution for the observational study on its own is
represents our uncertainty about the size of the observational bias. Larger values indicate more uncertainty. Standard Bayesian logic then shows that our posterior distribution for the observational study on its own is
![]() .
.
Now, under these assumptions, Bayes’ Theorem tells us how to combine the observational and experimental evidence, as Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 14) point out. In accordance with their argument, the resulting combined or aggregated estimate
![]() is a weighted average of the two estimates
is a weighted average of the two estimates
![]() and
and
![]() :
:
where p is the fraction of the weight given to the observational evidence, and
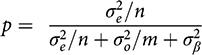 (6)
(6)
This result is the same as Gerber et al.’s, except that here we had no prior information about µ, which simplifies the interpretation without altering the implication that they wish to emphasize.
That implication is this: Since
![]() ,
,
![]() , n, and m are just features of the observed data, the key aspect of p is our uncertainty about the bias term
, n, and m are just features of the observed data, the key aspect of p is our uncertainty about the bias term
![]() , which is captured by the prior variance
, which is captured by the prior variance
![]() . Importantly, Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 15) argue that we often know relatively little about the size of likely biases in observational research. In the limit, they say, we become quite uncertain, and
. Importantly, Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 15) argue that we often know relatively little about the size of likely biases in observational research. In the limit, they say, we become quite uncertain, and
![]()
![]() . In that case, obviously,
. In that case, obviously,
![]() in Equation (6), and the observational evidence gets no weight at all in Equation (5), not even if its sample size is very large.
in Equation (6), and the observational evidence gets no weight at all in Equation (5), not even if its sample size is very large.
This limiting result is Reference Gerber, Green, Kaplan and TeeleGerber et al.’s (2014, 15) Illusion of Observational Learning Theorem. It formalizes the spirit of much recent commentary in the social sciences, in which observational studies are thought to be subject to biases of unknown, possibly very large size, whereas experiments follow textbook strictures and therefore reach unbiased estimates. Moreover, in an experiment, as the sample size goes to infinity, the correct average treatment effect is essentially learned with certainty.Footnote 2 Thus, only experiments tell us the truth. The mathematics here is unimpeachable, and the conclusion and its implications seem to be very powerful. Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 19–21) go on to demonstrate that under conditions like these, little or no resources should be allocated to observational research. We cannot learn anything from it. The money should go to field experiments such as those they have conducted, or to other experiments.
3.3 A Learning Theorem with No Thumb on the Scale
Gerber et al.’s Illusion of Observational Learning Theorem follows rigorously from their assumptions. The difficulty is that those assumptions combine jaundiced cynicism about observational studies with gullible innocence about experiments. As they make clear in the text, the authors themselves are neither unrelievedly cynical nor wholly innocent about either kind of research. But the logic of their mathematical conclusion turns out to depend entirely on their becoming sneering Mr. Hydes as they deal with observational research, and then transforming to kindly, indulgent Dr. Jekylls when they move to RCTs.
To see this, consider the standard challenge of experimental research: external validity, discussed in virtually every undergraduate methodology text (for example, Reference Kellstedt and WhittenKellstedt and Whitten 2009, 75–76). Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 22–23) mention this problem briefly, but they see it as a problem primarily for laboratory experiments because the inferential leap to the population is larger than for field experiments. The challenges that they identify for field experiments consist primarily in administering them properly. Even then, they suggest that statistical adjustments can often correct the biases induced (Reference Gerber, Green, Kaplan and TeeleGerber et al. 2014, 23–24). The flavor of their remarks may be seen in the following sentence:
The external validity of an experiment hinges on four factors: whether the subjects in the study are as strongly influenced by the treatment as the population to which a generalization is made, whether the treatment in the experiment corresponds to the treatment in the population of interest, whether the response measure used in the experiment corresponds to the variable of interest in the population, and how the effect estimates were derived statistically.
What is missing from this list are the two critical factors emphasized in the work of recent critics of RCTs: heterogeneity of treatment effects and the importance of context. A study of inducing voter turnout in a Michigan Republican primary cannot be generalized to what would happen to Democrats in a general election in Louisiana, where the treatment effects are likely to be very different. There are no Louisianans in the Michigan sample, no Democrats, and no general election voters. Hence, no within-sample statistical adjustments are available to accomplish the inferential leap. Biases of unknown magnitude remain, and these are multiplied when one aims to generalize to a national population as a whole. As Reference CartwrightCartwright (2007a; Chapter 2 this volume), Reference Cartwright and HardieCartwright and Hardie 2012, Reference DeatonDeaton (2010), and Reference Stokes and TeeleStokes (2014) have spelled out, disastrous inferential blunders occur commonly when a practitioner of field experiments imagines that they work the way Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014) assume that they work in their Bayesian model assumptions. Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 32 at fn. 6) concede in a footnote: “Whether bias creeps into an extrapolation to some other population depends on whether the effects vary across individuals in different contexts.” But that crucial insight plays no role in their mathematical model.
What happens in the Gerber et al. model when we take a more evenhanded approach? If we assume, for example, that experiments have a possible bias
![]() stemming from failures of external validity, then in parallel to the assumption about bias in observational research, we might specify our prior beliefs about external invalidity bias as normally and independently distributed:
stemming from failures of external validity, then in parallel to the assumption about bias in observational research, we might specify our prior beliefs about external invalidity bias as normally and independently distributed:
Then the posterior distribution of the treatment estimate from the experimental research would be
![]() , and the estimate combining both observational and experimental evidence would become:
, and the estimate combining both observational and experimental evidence would become:
where q is the new fraction of the weight given to the observational evidence, and
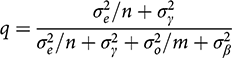 (9)
(9)
A close look at this expression (or taking partial derivatives) shows that the weight given to observational and experimental evidence is an intuitively plausible mix of considerations.
For example, an increase in m (the sample size of the observational study) reduces the denominator and thus raises q; this means that, all else equal, we should have more faith in observational studies with more observations. Conversely, increases in n, the sample size of an experiment, raise the weight we put on the experiment. In addition, the harder that authors have worked to eliminate confounders in observational research (small
![]() ), the more we believe them. And the fewer the issues with external validity in an experiment (small
), the more we believe them. And the fewer the issues with external validity in an experiment (small
![]() ), the more weight we put on the experiment. That is what follows from Gerber et al.’s line of analysis when all the potential biases are put on the table, not just half of them. But, of course, all these implications have been familiar for at least half a century. Carried out evenhandedly, the Bayesian mathematics does no real work and brings us no real news.
), the more weight we put on the experiment. That is what follows from Gerber et al.’s line of analysis when all the potential biases are put on the table, not just half of them. But, of course, all these implications have been familiar for at least half a century. Carried out evenhandedly, the Bayesian mathematics does no real work and brings us no real news.
Gerber et al. arrived at their Illusion of Observational Learning Theorem only by assuming away the problems of external validity in experiments. No surprise that experiments look wonderful in that case. But one could put a thumb on the other side of the scale: Suppose we assume that observational studies, when carefully conducted, have no biases due to omitted confounders, while experiments continue to have arbitrarily large problems with external validity. In that case,
![]() and
and
![]() . A look at Equations (8) and (9) then establishes that in that case, we get an Illusion of Experimental Learning Theorem: Experiments can teach us nothing, and no one should waste time and money on them. But of course, this inference is just as misleading as Gerber et al.’s original theorem.
. A look at Equations (8) and (9) then establishes that in that case, we get an Illusion of Experimental Learning Theorem: Experiments can teach us nothing, and no one should waste time and money on them. But of course, this inference is just as misleading as Gerber et al.’s original theorem.
Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014, 11–12, 15, 26–30) concede that observational research sometimes works very well. When observational biases are known to be small, they see a role for that kind of research. But they never discuss a similar condition for valid experimental studies. Even in their verbal discussions, which are more balanced than their mathematics, they continue to write as if experiments had no biases: “experiments produce unbiased estimates regardless of whether the confounders are known or unknown” (Reference Gerber, Green, Kaplan and TeeleGerber et al. 2014, 25). But that sentence is true only if external validity is never a problem. Their theorem about the unique value of experimental work depends critically on that assumption. Alas, the last decade or two have taught us forcefully, if we did not know it before, that their assumption is very far from being true. Just as instrumental variable estimators looked theoretically attractive when they were developed in the 1950s and 1960s but often failed in practice (Reference BartelsBartels 1991), so too the practical limitations of RCTs have now come forcefully into view.
Experiments have an important role in political science and in the social sciences generally. So do observational studies. But the judgment as to which of them is more valuable in a particular research problem depends on a complex mixture of prior experience, theoretical judgment, and the details of particular research designs. That is the conclusion that follows from an evenhanded set of assumptions applied to the model Reference Gerber, Green, Kaplan and TeeleGerber et al. (2014) set out.
3.4 Conclusion
Causal inference of any kind is just plain hard. If the evidence is observational, patient consideration of plausible counterarguments, followed by the assembling of relevant evidence, can be, and often is, a painstaking process.Footnote 3 Faced with those challenges, researchers in the current intellectual climate may be tempted to substitute something that looks quicker and easier – an experiment.
The central argument for experiments (RCTs) is that the randomization produces identification of the key parameter. That is a powerful and seductive idea, and it works very well in textbooks. Alas, this modus operandi does not work nearly so well in practice. Without an empirical or theoretical understanding of how to get from experimental results to the relevant population of interest, stand-alone RCTs teach us just as little as casual observational studies. In either case, there is no royal road to secure inferences, as Nancy Cartwright has emphasized. Hard work and provisional findings are all we can expect. As Reference CartwrightCartwright (2007b) has pungently remarked, experiments are not the gold standard, because there is no gold standard.

