Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-17T16:50:11.572Z Has data issue: false hasContentIssue false
  • English
  • Français

Parabolic induction and restriction via 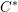$C^{\ast }$-algebras and Hilbert 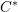$C^{\ast }$-modules

Part of: Selfadjoint operator algebras Lie groups Locally compact groups and their algebras

Published online by Cambridge University Press:  02 February 2016

Pierre Clare ,
Tyrone Crisp  and
Nigel Higson
Pierre Clare
Affiliation:
Dartmouth College, Department of Mathematics, HB 6188, Hanover, NH 03755, USA email [email protected]
Tyrone Crisp
Affiliation:
Max-Planck-Institut für Mathematik, Vivatsgasse 7, 53111 Bonn, Germany email [email protected]
Nigel Higson
Affiliation:
Pennsylvania State University, Department of Mathematics, University Park, PA 16802, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is about the reduced group 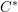$C^{\ast }$-algebras of real reductive groups, and about Hilbert 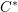$C^{\ast }$-modules over these 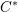$C^{\ast }$-algebras. We shall do three things. First, we shall apply theorems from the tempered representation theory of reductive groups to determine the structure of the reduced 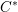$C^{\ast }$-algebra (the result has been known for some time, but it is difficult to assemble a full treatment from the existing literature). Second, we shall use the structure of the reduced 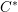$C^{\ast }$-algebra to determine the structure of the Hilbert 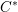$C^{\ast }$-bimodule that represents the functor of parabolic induction. Third, we shall prove that the parabolic induction bimodule admits a secondary inner product, using which we can define a functor of parabolic restriction in tempered representation theory. We shall prove in a sequel to this paper that parabolic restriction is adjoint, on both the left and the right, to parabolic induction in the context of tempered unitary Hilbert space representations.

Keywords

tempered representationsparabolic inductionuniversal principal seriesparabolic restrictionreduced group C∗ -algebras

MSC classification

Primary: 22E45: Representations of Lie and linear algebraic groups over real fields 22D25: $C^*$-algebras and $W^*$-algebras in relation to group representations 46L08: $C^*$-modules
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 6 , June 2016 , pp. 1286 - 1318
Copyright
© The Authors 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, J., A theorem on the Schwartz space of a reductive Lie group, Proc. Natl. Acad. Sci. USA 72 (1975), 4718–4719; MR 0460539 (57 #532).Google Scholar
Arthur, J., A Paley–Wiener theorem for real reductive groups, Acta Math. 150 (1983), 1–89; MR 697608 (84k:22021).CrossRefGoogle Scholar
Baum, P., Connes, A. and Higson, N., Classifying space for proper actions and K-theory of group C ∗ -algebras, C ∗ -algebras: 1943–1993 (San Antonio, TX, 1993), Contemporary Mathematics, vol. 167 (American Mathematical Society, Providence, RI, 1994), 240–291; MR 1292018 (96c:46070).Google Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazhdan’s property (T), New Mathematical Monographs, vol. 11 (Cambridge University Press, Cambridge, 2008).Google Scholar
Bernstein, J., Representations of p-adic groups, Lecture Notes (Harvard University, 1992); written by K. E. Rumelhart.Google Scholar
Bezrukavnikov, R. and Kazhdan, D., Geometry of second adjointness for p-adic groups, Represent. Theory 19 (2015), 299–332.Google Scholar
Boyer, R. and Martin, R., The regular group C ∗ -algebra for real-rank one groups, Proc. Amer. Math. Soc. 59 (1976), 371–376; MR 0476913 (57 #16464).Google Scholar
Bruhat, F., Sur les reprsentations induites des groupes de Lie, Bull. Soc. Math. France 84 (1956), 97–205.Google Scholar
Clare, P., Hilbert modules associated to parabolically induced representations, J. Operator Theory 69 (2013), 483–509; MR 3053351.CrossRefGoogle Scholar
Clare, P., C ∗ -algebraic intertwiners for degenerate principal series of special linear groups, Chin. Ann. Math. Ser. B 35 (2014), 691–702; MR 3246931.Google Scholar
Clare, P., C ∗ -algebraic intertwiners for principal series: case of SL (2), J. Noncommut. Geom. 9 (2015), 1–19; MR 3337952.Google Scholar
Clare, P., Crisp, T. and Higson, N., Adjoint functors between categories of Hilbert $C^{\ast }$-modules, Preprint (2014), arXiv:1409.8656.Google Scholar
Cowling, M., Haagerup, U. and Howe, R., Almost L 2 matrix coefficients, J. Reine Angew. Math. 387 (1988), 97–110; MR 946351 (89i:22008).Google Scholar
Crisp, T. and Higson, N., Parabolic induction, categories of representations and operator spaces, in Operator algebras and their applications: a tribute to Richard V. Kadison, Contemporary Mathematics, vol. 671 (American Mathematical Society, Providence, RI, 2016), to appear.Google Scholar
Dixmier, J., Sur les représentations unitaires des groupes de Lie algébriques, Ann. Inst. Fourier (Grenoble) 7 (1957), 315–328; MR 0099380 (20 #5820).Google Scholar
Dixmier, J., C ∗ -algebras, North-Holland Mathematical Library, vol. 15 (North-Holland, Amsterdam, 1977); translated from the French by Francis Jellett; MR 0458185 (56 #16388).Google Scholar
Fell, J. M. G., The dual spaces of C ∗ -algebras, Trans. Amer. Math. Soc. 94 (1960), 365–403; MR 0146681 (26 #4201).Google Scholar
Godement, R., A theory of spherical functions I, Trans. Amer. Math. Soc. 73 (1952), 496–556.Google Scholar
Harish-Chandra, Representations of semisimple Lie groups on a Banach space I, Trans. Amer. Math. Soc. 75 (1953), 185–243.Google Scholar
Harish-Chandra, Discrete series for semisimple Lie groups. II. Explicit determination of the characters, Acta Math. 116 (1966), 1–111; MR 0219666 (36 #2745).CrossRefGoogle Scholar
Harish-Chandra, On the theory of the Eisenstein integral, Lecture Notes in Mathematics, vol. 266(Springer, New York, 1972), 123–149.Google Scholar
Harish-Chandra, Harmonic analysis on real reductive groups III. The Maaß–Selberg relations and the Plancherel formula, Ann. of Math. (2) 104 (1976), 117–201.Google Scholar
Humphreys, J. E., Linear algebraic groups, Graduate Texts in Mathematics, vol. 21 (Springer, New York, 1975); MR 0396773 (53 #633).CrossRefGoogle Scholar
Knapp, A. W., Representation theory of semisimple groups, Princeton Landmarks in Mathematics (Princeton University Press, Princeton, NJ, 1986).Google Scholar
Knapp, A. W., Lie groups beyond an introduction, Progress in Mathematics, vol. 140, second edition (Birkhäuser, Boston, 2002).Google Scholar
Knapp, A. W. and Stein, E. M., Irreducibility theorems for the principal series, in Conference on Harmonic Analysis (College Park, Maryland, 1971), Lecture Notes in Mathematics, vol. 266 (Springer, Berlin, 1972), 197–214; MR 0422512 (54 #10499).Google Scholar
Knapp, A. W. and Stein, E. M., Intertwining operators for semisimple groups II, Invent. Math. 60 (1980), 9–84.Google Scholar
Lance, E. C., Hilbert C*-modules, LMS Lecture Note Series (Cambridge University Press, Cambridge, 1995).Google Scholar
Langlands, R. P., On the classification of irreducible representations of real algebraic groups, in Representation theory and harmonic analysis on semisimple Lie groups, Mathematical Surveys Monographs, vol. 31 (American Mathematical Society, Providence, RI, 1989), 101–170; MR 1011897 (91e:22017).Google Scholar
Lipsman, R. L., The dual topology for the principal and discrete series on semisimple groups, Trans. Amer. Math. Soc. 152 (1970), 399–417; MR 0269778 (42 #4673).Google Scholar
Miličić, D., On C ∗ -algebras with bounded trace, Glas. Mat. Ser. III 8(28) (1973), 7–22; MR 0324429 (48 #2781).Google Scholar
Miličić, D. and Primc, M., On the irreducibility of unitary principal series representations, Math. Ann. 260(4) (1982), 413–421; MR 670190 (84c:22019).Google Scholar
Pedersen, G. K., C ∗ -algebras and their automorphism groups, London Mathematical Society Monographs, vol. 14 (Academic Press, London, 1979); MR 548006 (81e:46037).Google Scholar
Penington, M. G. and Plymen, R. J., The Dirac operator and the principal series for complex semisimple Lie groups, J. Funct. Anal. 53 (1983), 269–286; MR 724030 (85d:22016).Google Scholar
Rieffel, M. A., Induced representations of C*-algebras, Adv. Math. 13 (1974), 176–257.CrossRefGoogle Scholar
Stinespring, W. F., A semi-simple matrix group is of type I, Proc. Amer. Math. Soc. 9 (1958), 965–967; MR 0104756 (21 #3509).Google Scholar
Trombi, P. C., The tempered spectrum of a real semisimple Lie group, Amer. J. Math. 99 (1977), 57–75; MR 0453929 (56 #12182).Google Scholar
Valette, A., Dirac induction for semi-simple Lie groups having one conjugacy class of Cartan subgroups, in Operator algebras and their connections with topology and ergodic theory, Lecture Notes in Mathematics, vol. 1132, eds Araki, H., Moore, C. C., Stratila, S.-V. and Voiculescu, D.-V. (Springer, Berlin, 1985), 526–555.Google Scholar
Vogan, D. A. Jr., Representations of real reductive Lie groups, Progress in Mathematics, vol. 15 (Birkhäuser, Boston, 1981); MR 632407 (83c:22022).Google Scholar
Wallach, N. R., Real reductive groups. I, Pure and Applied Mathematics, vol. 132 (Academic Press, Boston, 1988); MR 929683 (89i:22029).Google Scholar
Wallach, N. R., Real reductive groups. II, Pure and Applied Mathematics, vol. 132-II (Academic Press, Boston, 1992); MR 1170566 (93m:22018).Google Scholar
Wassermann, A., Une démonstration de la conjecture de Connes–Kasparov pour les groupes de Lie linaires connexes rductifs, C. R. Acad. Sci. Paris 18 (1987), 559–562.Google Scholar