Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-17T17:15:26.088Z Has data issue: false hasContentIssue false
  • English
  • Français

On finite groups with exactly one vanishing conjugacy class size

Part of: Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  15 February 2022

Neda Ahanjideh Open the ORCID record for Neda Ahanjideh [Opens in a new window]
Neda Ahanjideh*
Affiliation:
Department of Pure Mathematics, Faculty of Mathematical Sciences, Shahrekord University, P. O. Box 115, Shahrekord, Iran ([email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $G$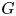 be a finite group. An element $g \in G$ 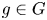is called a vanishing element in $G$ 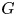if there exists an irreducible character $\chi$ 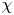of $G$ 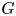such that $\chi (g)=0$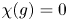. The size of a conjugacy class of $G$ 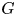containing a vanishing element is called a vanishing conjugacy class size of $G$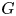. In this paper, we give an affirmative answer to the problem raised by Bianchi, Camina, Lewis and Pacifici about the solvability of finite groups with exactly one vanishing conjugacy class size.

Keywords

Conjugacy class sizesirreducible charactersvanishing elements

MSC classification

Primary: 20E45: Conjugacy classes
Secondary: 20C15: Ordinary representations and characters 20D05: Finite simple groups and their classification
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 1 , February 2023 , pp. 344 - 368
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahanjideh, N.. A Criterion for the existence of nilpotent Hall $\pi$-subgroups. J. Algebra Appl. 2020. DOI:10.1142/S0219498822500438Google Scholar
Bianchi, M., Camina, R. D., Lewis, M. L. and Pacifici, E.. On solvable groups with one vanishing class size. Proc. R. Soc. Edinb. Sec. A: Math. 151 (2021), 1467–1486.CrossRefGoogle Scholar
Casolo, C., Dolfi, S. and Jabara, E.. Finite groups whose noncentral class sizes have the same $p$-part for some prime $p$. Isr. J. Math. 192 (2012), 197–219.CrossRefGoogle Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A.. Atlas of finite groups (London: Oxford University Press, 1984).Google Scholar
Dolfi, S., Navarro, G., Pacifici, E., Sanus, L. and Tiep, P. H.. Non-vanishing elements of finite groups. J. Algebra 323 (2010), 540–545.CrossRefGoogle Scholar
Dolfi, S., Pacifici, E. and Sanus, L.. Groups whose vanishing class sizes are not divisible by a given prime. Arch. Math. 94 (2010), 311–317.CrossRefGoogle Scholar
Dolfi, S., Pacifici, E., Sanus, L. and Spiga, P.. On the vanishing prime graph of finite groups. J. Lond. Math. Soc. 82 (2010), 167–183.CrossRefGoogle Scholar
Feit, W.. On large Zsigmondy primes. Proc. Am. Math. Soc. 102 (1988), 29–36.CrossRefGoogle Scholar
Gorenstein, D.. Finite groups (New York, London: American Mathematical Soc., 1968).Google Scholar
Granville, A. and Ono, K.. Defect zero $p$-blocks for finite simple groups. Trans. Am. Math. Soc. 348 (1996), 331–347.CrossRefGoogle Scholar
Huppert, B., Character theory of finite groups, Vol. 25, De Gruyter, Expositions in Mathematics (Berlin, 1998).CrossRefGoogle Scholar
Huppert, B.. Endliche gruppen I (Springer, Berlin, 1967).CrossRefGoogle Scholar
Isaacs, I. M.. Groups with many equal classes. Duke Math. J. 37 (1970), 501–506.CrossRefGoogle Scholar
Isaacs, I. M., Navarro, G. and Wolf, T. R.. Finite group elements where no irreducible character vanishes. J. Algebra 222 (1999), 413–423.CrossRefGoogle Scholar
Kondratev, A. S. and Mazurov, V. D.. Recognition of alternating groups of prime degree from their element orders. Sib. Math. J. 41 (2000), 294–302.CrossRefGoogle Scholar
Kurzweil, K. and Stellmacher, B.. The theory of finite groups. An introduction (New York: Springer-Verlag, 2004).CrossRefGoogle Scholar
Vasiliev, A. V. and Vdovin, E. P.. An adjacency criterion for the prime graph of a finite simple group. Algebra Logic 44 (2005), 381–406.CrossRefGoogle Scholar