Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-25T17:44:53.244Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME CRITERIA FOR SOLVABILITY AND NILPOTENCY OF FINITE GROUPS BY STRONGLY MONOLITHIC CHARACTERS

Part of: Representation theory of groups

Published online by Cambridge University Press:  22 September 2022

SULTAN BOZKURT GÜNGÖR Open the ORCID record for SULTAN BOZKURT GÜNGÖR [Opens in a new window]  and
TEMHA ERKOÇ Open the ORCID record for TEMHA ERKOÇ [Opens in a new window]
SULTAN BOZKURT GÜNGÖR
Affiliation:
Department of Mathematics, Faculty of Science, Istanbul University, 34134 Istanbul, Turkey e-mail: [email protected]
TEMHA ERKOÇ*
Affiliation:
Department of Mathematics, Faculty of Science, Istanbul University, 34134 Istanbul, Turkey
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Gagola and Lewis [‘A character theoretic condition characterizing nilpotent groups’, Comm. Algebra 27 (1999), 1053–1056] proved that a finite group G is nilpotent if and only if 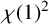$\chi (1)^{2}$ divides 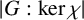$\lvert G:\textrm {ker}\,\chi \rvert $ for every irreducible character 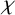$\chi $ of G. The theorem was later generalised by using monolithic characters. We generalise the theorem further considering only strongly monolithic characters. We also give some criteria for solvability and nilpotency of finite groups by their strongly monolithic characters.

Keywords

finite groupsolvable groupnilpotent groupstrongly monolithic character

MSC classification

Primary: 20C15: Ordinary representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 120 - 124
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work of the authors was supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK), project number 119F295.

References

Berkovich, Y. G., ‘On Isaacs’ three character degrees theorem’, Proc. Amer. Math. Soc. 125(3) (1997), 669–677.CrossRefGoogle Scholar
Berkovich, Y. G. and Zhmud, E. M., Characters of Finite Groups. Part II, Translations of Mathematical Monographs, 181 (American Mathematical Society, Providence, RI, 1997).CrossRefGoogle Scholar
Erkoç, T., Güngör, S. B. and Özkan, J. M., ‘Strongly monolithic characters of finite groups’, J. Algebra Appl., to appear. Published online (28 May 2022).Google Scholar
Gagola, S. M. and Lewis, M. L., ‘A character theoretic condition characterizing nilpotent groups’, Comm. Algebra 27 (1999), 1053–1056.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Isaacs, I. M., ‘Large orbits in actions of nilpotent groups’, Proc. Amer. Math. Soc. 127(1) (1999), 45–50.CrossRefGoogle Scholar
Isaacs, I. M., Algebra: A Graduate Course, Graduate Studies in Mathematics, 100 (American Mathematical Society, Providence, RI, 2009).CrossRefGoogle Scholar
Isaacs, I. M. and Knutson, G., ‘Irreducible character degrees and normal subgroups’, J. Algebra 199(1) (1998), 302–326.CrossRefGoogle Scholar
Isaacs, I. M. and Passman, D. S., ‘A characterization of groups in terms of the degrees of their characters II’, Pacific J. Math. 24(3) (1968), 467–510.CrossRefGoogle Scholar
Lu, J., Qin, X. and Liu, X., ‘Generalizing a theorem of Gagola and Lewis characterizing nilpotent groups’, Arch. Math. 108 (2017), 337–339.CrossRefGoogle Scholar