Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-17T18:55:45.188Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE LOWEST EIGENVALUE OF THE FRACTIONAL LAPLACIAN FOR THE INTERSECTION OF TWO DOMAINS

Part of: Partial differential operators Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  02 December 2022

ANH TUAN DUONG Open the ORCID record for ANH TUAN DUONG [Opens in a new window]  and
VAN HOANG NGUYEN Open the ORCID record for VAN HOANG NGUYEN [Opens in a new window]
ANH TUAN DUONG*
Affiliation:
School of Applied Mathematics and Informatics, Hanoi University of Science and Technology, 1 Dai Co Viet, Hai Ba Trung, Ha Noi, Vietnam
VAN HOANG NGUYEN
Affiliation:
Department of Mathematics, FPT University, Ha Noi, Vietnam e-mail: [email protected] and [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend a result of Lieb [‘On the lowest eigenvalue of the Laplacian for the intersection of two domains’, Invent. Math. 74(3) (1983), 441–448] to the fractional setting. We prove that if A and B are two bounded domains in 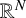$\mathbb R^N$ and 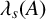$\lambda _s(A)$, 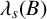$\lambda _s(B)$ are the lowest eigenvalues of 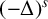$(-\Delta )^s$, 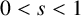$0<s<1$, with Dirichlet boundary conditions, there exists some translation 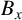$B_x$ of B such that 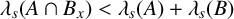$\lambda _s(A\cap B_x)< \lambda _s(A)+\lambda _s(B)$. Moreover, without the boundedness assumption on A and B, we show that for any 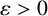$\varepsilon>0$, there exists some translation 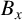$B_x$ of B such that 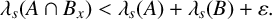$\lambda _s(A\cap B_x)< \lambda _s(A)+\lambda _s(B)+\varepsilon .$

Keywords

lowest eigenvaluefractional Laplacianintersection of two domainseigenvalue problem

MSC classification

Primary: 35P15: Estimation of eigenvalues, upper and lower bounds
Secondary: 47F05: Partial differential operators (should also be assigned at least one other classification number in section 47)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 290 - 297
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellazzini, J., Frank, R. L. and Visciglia, N., ‘Maximizers for Gagliardo–Nirenberg inequalities and related non-local problems’, Math. Ann. 360(3–4) (2014), 653–673.10.1007/s00208-014-1046-2CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E., ‘Hitchhiker’s guide to the fractional Sobolev spaces’, Bull. Sci. Math. 136(5) (2012), 521–573.10.1016/j.bulsci.2011.12.004CrossRefGoogle Scholar
Faber, G., ‘Beweis, daß unter allen homogenen membranen von gleicher fläche und gleicher spannung die kreisförmige den tiefsten grundton gibt’, Sitzungsber. Bayer. Akad. Wiss. München, Math.-Phys. Kl. 1923(8) (1923), 169–172.Google Scholar
Frank, R. L., ‘Eigenvalue bounds for the fractional Laplacian: a review’, in: Recent Developments in Nonlocal Theory (eds. Palatucci, G. and Kuusi, T.) (De Gruyter, Berlin, 2018), 210–235.Google Scholar
Krahn, E., ‘Über eine von Rayleigh formulierte Minimaleigenschaft des Kreises’, Math. Ann. 94(1) (1925), 97–100.10.1007/BF01208645CrossRefGoogle Scholar
Lieb, E. H., ‘On the lowest eigenvalue of the Laplacian for the intersection of two domains’, Invent. Math. 74(3) (1983), 441–448.10.1007/BF01394245CrossRefGoogle Scholar