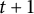For a nondegenerate r-graph F, large n, and t in the regime $[0, c_{F} n]$, where $c_F>0$ is a constant depending only on F, we present a general approach for determining the maximum number of edges in an n-vertex r-graph that does not contain 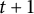$t+1$ vertex-disjoint copies of F. In fact, our method results in a rainbow version of the above result and includes a characterization of the extremal constructions.

Our approach applies to many well-studied hypergraphs (including graphs) such as the edge-critical graphs, the Fano plane, the generalized triangles, hypergraph expansions, the expanded triangles, and hypergraph books. Our results extend old results of Erdős [13], Simonovits [76], and Moon [58] on complete graphs, and can be viewed as a step toward a general density version of the classical Corrádi–Hajnal [10] and Hajnal–Szemerédi [32] theorems.

Our method relies on a novel understanding of the general properties of nondegenerate Turán problems, which we refer to as smoothness and boundedness. These properties are satisfied by a broad class of nondegenerate hypergraphs and appear to be worthy of future exploration.