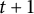1 Introduction
1.1 Motivation
Fix an integer
![]() $r\ge 2$
, an r-graph
$r\ge 2$
, an r-graph
![]() $\mathcal {H}$
is a collection of r-subsets of some finite set V. We identify a hypergraph
$\mathcal {H}$
is a collection of r-subsets of some finite set V. We identify a hypergraph
![]() $\mathcal {H}$
with its edge set and use
$\mathcal {H}$
with its edge set and use
![]() $V(\mathcal {H})$
to denote its vertex set. The size of
$V(\mathcal {H})$
to denote its vertex set. The size of
![]() $V(\mathcal {H})$
is denoted by
$V(\mathcal {H})$
is denoted by
![]() $v(\mathcal {H})$
.
$v(\mathcal {H})$
.
Given two r-graphs F and
![]() $\mathcal {H}$
we use
$\mathcal {H}$
we use
![]() $\nu (F, \mathcal {H})$
to denote the maximum of
$\nu (F, \mathcal {H})$
to denote the maximum of
![]() $k\in \mathbb {N}$
such that there exist k vertex-disjoint copies of F in
$k\in \mathbb {N}$
such that there exist k vertex-disjoint copies of F in
![]() $\mathcal {H}$
. We call
$\mathcal {H}$
. We call
![]() $\nu (F, \mathcal {H})$
the F-matching number of
$\nu (F, \mathcal {H})$
the F-matching number of
![]() $\mathcal {H}$
. If
$\mathcal {H}$
. If
![]() $F = K_{r}^{r}$
(i.e., an edge), then we use
$F = K_{r}^{r}$
(i.e., an edge), then we use
![]() $\nu (\mathcal {H})$
to represent
$\nu (\mathcal {H})$
to represent
![]() $\nu (F, \mathcal {H})$
for simplicity. The number
$\nu (F, \mathcal {H})$
for simplicity. The number
![]() $\nu (\mathcal {H})$
is also known as the matching number of
$\nu (\mathcal {H})$
is also known as the matching number of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
The study of the following problem encompasses several central topics in Extremal Combinatorics. Given an r-graph F and integers
![]() $n, t\in \mathbb {N}$
:
$n, t\in \mathbb {N}$
:
For
![]() $r=2$
and
$r=2$
and
![]() $F = K_{2}$
, the celebrated Erdős–Gallai theorem [Reference Erdős and Gallai15] states that for all integers
$F = K_{2}$
, the celebrated Erdős–Gallai theorem [Reference Erdős and Gallai15] states that for all integers
![]() $n, \ell \in \mathbb {N}$
with
$n, \ell \in \mathbb {N}$
with
![]() $t+1 \le n/2$
and for every n-vertex graph G,
$t+1 \le n/2$
and for every n-vertex graph G,
Here, we use the symbol
![]() $\Rightarrow $
to indicate that the constraint on the left side forces the conclusion on the right side.
$\Rightarrow $
to indicate that the constraint on the left side forces the conclusion on the right side.
Extending the Erdős–Gallai theorem to r-graphs for
![]() $r\ge 3$
is a major open problem, and the following conjecture of Erdős is still open in general (see, e.g., [Reference Frankl21–Reference Frankl23, Reference Huang, Loh and Sudakov38] for some recent progress on this topic).
$r\ge 3$
is a major open problem, and the following conjecture of Erdős is still open in general (see, e.g., [Reference Frankl21–Reference Frankl23, Reference Huang, Loh and Sudakov38] for some recent progress on this topic).
Conjecture 1.1 (Erdős [Reference Erdős14])
Suppose that
![]() $n, t, r \in \mathbb {N}$
satisfy
$n, t, r \in \mathbb {N}$
satisfy
![]() $r\ge 3$
and
$r\ge 3$
and
![]() $t+1 \le n/r$
. Then for every n-vertex r-graph
$t+1 \le n/r$
. Then for every n-vertex r-graph
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
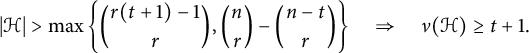 $$ \begin{align*} |\mathcal{H}|> \max\left\{\binom{r(t+1)-1}{r}, \binom{n}{r}-\binom{n-t}{r}\right\} \quad\Rightarrow\quad \nu(\mathcal{H}) \ge t+1. \end{align*} $$
$$ \begin{align*} |\mathcal{H}|> \max\left\{\binom{r(t+1)-1}{r}, \binom{n}{r}-\binom{n-t}{r}\right\} \quad\Rightarrow\quad \nu(\mathcal{H}) \ge t+1. \end{align*} $$
For general r-graphs F, determining the minimum number of edges in an n-vertex r-graph
![]() $\mathcal {H}$
that guarantees
$\mathcal {H}$
that guarantees
![]() $\nu (F,\mathcal {H}) \ge 1$
is closely related to the Turán problem. For our purpose in this work, let us introduce the following notions.
$\nu (F,\mathcal {H}) \ge 1$
is closely related to the Turán problem. For our purpose in this work, let us introduce the following notions.
Fix an r-graph F, we say another r-graph
![]() $\mathcal {H}$
is F-free if
$\mathcal {H}$
is F-free if
![]() $\nu (F,\mathcal {H}) = 0$
. In other words,
$\nu (F,\mathcal {H}) = 0$
. In other words,
![]() $\mathcal {H}$
does not contains F as a subgraph. The Turán number
$\mathcal {H}$
does not contains F as a subgraph. The Turán number
![]() $\mathrm {ex}(n,F)$
of F is the maximum number of edges in an F-free r-graph on n vertices. The Turán density of F is defined as
$\mathrm {ex}(n,F)$
of F is the maximum number of edges in an F-free r-graph on n vertices. The Turán density of F is defined as
![]() $\pi (F) := \lim _{n\to \infty }\mathrm {ex}(n,F)/\binom {n}{r}$
, the existence of the limit follows from a simple averaging argument of Katona, Nemetz, and Simonovits [Reference Katona, Nemetz and Simonovits41] (see Proposition 3.2).
$\pi (F) := \lim _{n\to \infty }\mathrm {ex}(n,F)/\binom {n}{r}$
, the existence of the limit follows from a simple averaging argument of Katona, Nemetz, and Simonovits [Reference Katona, Nemetz and Simonovits41] (see Proposition 3.2).
An r-graph F is called nondegenerate if
![]() $\pi (F)> 0$
. We use
$\pi (F)> 0$
. We use
![]() $\mathrm {EX}(n,F)$
to denote the collection of all n-vertex F-free r-graphs with exactly
$\mathrm {EX}(n,F)$
to denote the collection of all n-vertex F-free r-graphs with exactly
![]() $\mathrm {ex}(n,F)$
edges, and call members in
$\mathrm {ex}(n,F)$
edges, and call members in
![]() $\mathrm {EX}(n,F)$
the extremal constructions of F. The study of
$\mathrm {EX}(n,F)$
the extremal constructions of F. The study of
![]() $\mathrm {ex}(n,F)$
and
$\mathrm {ex}(n,F)$
and
![]() $\mathrm {EX}(n,F)$
is a central topic in Extremal Combinatorics.
$\mathrm {EX}(n,F)$
is a central topic in Extremal Combinatorics.
Much is known when
![]() $r=2$
, and one of the earliest results in this regard is Mantel’s theorem [Reference Mantel57], which states that
$r=2$
, and one of the earliest results in this regard is Mantel’s theorem [Reference Mantel57], which states that
![]() $\mathrm {ex}(n,K_3) = \lfloor n^2/4 \rfloor $
. For every integer
$\mathrm {ex}(n,K_3) = \lfloor n^2/4 \rfloor $
. For every integer
![]() $\ell \ge 2$
let
$\ell \ge 2$
let
![]() $T(n,\ell )$
denote the balanced complete
$T(n,\ell )$
denote the balanced complete
![]() $\ell $
-partite graph on n vertices. Here, balanced means that the sizes of any two parts differ by at most one. We call
$\ell $
-partite graph on n vertices. Here, balanced means that the sizes of any two parts differ by at most one. We call
![]() $T(n,\ell )$
the Turán graph, and use
$T(n,\ell )$
the Turán graph, and use
![]() $t(n,\ell )$
to denote the number of edges in
$t(n,\ell )$
to denote the number of edges in
![]() $T(n,\ell )$
. The seminal Turán theorem states that
$T(n,\ell )$
. The seminal Turán theorem states that
![]() $\mathrm {EX}(n, K_{\ell +1}) = \{T(n,\ell )\}$
for all integers
$\mathrm {EX}(n, K_{\ell +1}) = \{T(n,\ell )\}$
for all integers
![]() $n \ge \ell \ge 2$
. Later, Turán’s theorem was extended to general graphs F in the celebrated Erdős–Stone–Simonovits theorem [Reference Erdős and Simonovits16, Reference Erdős and Stone18], which says that
$n \ge \ell \ge 2$
. Later, Turán’s theorem was extended to general graphs F in the celebrated Erdős–Stone–Simonovits theorem [Reference Erdős and Simonovits16, Reference Erdős and Stone18], which says that
![]() $\pi (F) = \left (\chi (F)-2\right )/\left (\chi (F)-1\right )$
. Here
$\pi (F) = \left (\chi (F)-2\right )/\left (\chi (F)-1\right )$
. Here
![]() $\chi (F)$
is the chromatic number of F.
$\chi (F)$
is the chromatic number of F.
For
![]() $r\ge 3$
, determining
$r\ge 3$
, determining
![]() $\mathrm {ex}(n, F)$
or even
$\mathrm {ex}(n, F)$
or even
![]() $\pi (F)$
for an r-graph F is known to be notoriously hard in general. The problem of determining
$\pi (F)$
for an r-graph F is known to be notoriously hard in general. The problem of determining
![]() $\pi (K_{\ell }^{r})$
raised by Turán [Reference Turán78], where
$\pi (K_{\ell }^{r})$
raised by Turán [Reference Turán78], where
![]() $K_{\ell }^{r}$
is the complete r-graph on
$K_{\ell }^{r}$
is the complete r-graph on
![]() $\ell $
vertices, is still wide open for all
$\ell $
vertices, is still wide open for all
![]() $\ell>r\ge 3$
. Erdős offered $
$\ell>r\ge 3$
. Erdős offered $
![]() $500$
for the determination of any
$500$
for the determination of any
![]() $\pi (K_{\ell }^{r})$
with
$\pi (K_{\ell }^{r})$
with
![]() $\ell> r \ge 3$
and
$\ell> r \ge 3$
and
![]() $\$ 1000$
for all
$\$ 1000$
for all
![]() $\pi (K_{\ell }^{r})$
with
$\pi (K_{\ell }^{r})$
with
![]() $\ell> r \ge 3$
. We refer the reader to an excellent survey [Reference Keevash42] by Keevash for related results before 2011.
$\ell> r \ge 3$
. We refer the reader to an excellent survey [Reference Keevash42] by Keevash for related results before 2011.
Another related central topic in Extremal Combinatorics is the Factor Problem. We say an r-graph
![]() $\mathcal {H}$
has an F-factor if it contains a collection of vertex-disjoint copies of F that covers all vertices in
$\mathcal {H}$
has an F-factor if it contains a collection of vertex-disjoint copies of F that covers all vertices in
![]() $V(\mathcal {H})$
. In other words,
$V(\mathcal {H})$
. In other words,
![]() $\nu (F, \mathcal {H}) = \frac {v(\mathcal {H})}{v(F)}$
(in particular,
$\nu (F, \mathcal {H}) = \frac {v(\mathcal {H})}{v(F)}$
(in particular,
![]() $v(F) \mid v(\mathcal {H})$
).
$v(F) \mid v(\mathcal {H})$
).
For an r-graph
![]() $\mathcal {H}$
and a vertex
$\mathcal {H}$
and a vertex
![]() $v\in V(\mathcal {H})$
the degree
$v\in V(\mathcal {H})$
the degree
![]() $d_{\mathcal {H}}(v)$
of v in
$d_{\mathcal {H}}(v)$
of v in
![]() $\mathcal {H}$
is the number of edges in
$\mathcal {H}$
is the number of edges in
![]() $\mathcal {H}$
containing v. We use
$\mathcal {H}$
containing v. We use
![]() $\delta (\mathcal {H})$
,
$\delta (\mathcal {H})$
,
![]() $\Delta (\mathcal {H})$
, and
$\Delta (\mathcal {H})$
, and
![]() $d(\mathcal {H})$
to denote the minimum degree, the maximum degree, and the average degree of
$d(\mathcal {H})$
to denote the minimum degree, the maximum degree, and the average degree of
![]() $\mathcal {H}$
, respectively. We will omit the subscript
$\mathcal {H}$
, respectively. We will omit the subscript
![]() $\mathcal {H}$
if it is clear from the context.
$\mathcal {H}$
if it is clear from the context.
A classical theorem of Corrádi and Hajnal [Reference Corradi and Hajnal10] implies the following result for
![]() $K_3$
.
$K_3$
.
Theorem 1.2 (Corrádi–Hajnal [Reference Corradi and Hajnal10])
Suppose that
![]() $n, t \in \mathbb {N}$
are integers with
$n, t \in \mathbb {N}$
are integers with
![]() $t\le n/3$
. Then for every n-vertex graph G,
$t\le n/3$
. Then for every n-vertex graph G,
In particular, if
![]() $3 \mid n$
, then every n-vertex graph G with
$3 \mid n$
, then every n-vertex graph G with
![]() $\delta (G) \ge 2n/3$
contains a
$\delta (G) \ge 2n/3$
contains a
![]() $K_3$
-factor.
$K_3$
-factor.
Later, Theorem 1.2 was extended to all complete graphs in the classical Hajnal–Szemerédi theorem [Reference Hajnal and Szemerédi32], which implies that for all integers
![]() $n\ge \ell \ge 2$
,
$n\ge \ell \ge 2$
,
![]() $t \le \lfloor n/(\ell +1) \rfloor $
, and for every n-vertex graph G,
$t \le \lfloor n/(\ell +1) \rfloor $
, and for every n-vertex graph G,
For further related results, we refer the reader to a survey [Reference Kühn and Osthus48] by Kühn and Osthus.
In this work, we are interested in density constraints that force an r-graph to have large F-matching number, where F is a nondegenerate r-graph. Since our results are closely related to the Turán problem of F, we abuse the use of notation by letting
![]() $\mathrm {ex}\left (n, (t+1)F\right )$
denote the maximum number of edges in an n-vertex r-graph
$\mathrm {ex}\left (n, (t+1)F\right )$
denote the maximum number of edges in an n-vertex r-graph
![]() $\mathcal {H}$
with
$\mathcal {H}$
with
![]() $\nu (F, \mathcal {H}) < t+1$
.
$\nu (F, \mathcal {H}) < t+1$
.
Given two r-graphs
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {H}$
whose vertex sets are disjoint, we define the join
$\mathcal {H}$
whose vertex sets are disjoint, we define the join ![]() of
of
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {H}$
to be the r-graph obtained from
$\mathcal {H}$
to be the r-graph obtained from
![]() $\mathcal {G}\sqcup \mathcal {H}$
(the vertex-disjoint union of
$\mathcal {G}\sqcup \mathcal {H}$
(the vertex-disjoint union of
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathcal {H}$
) by adding all r-sets that have nonempty intersection with both
$\mathcal {H}$
) by adding all r-sets that have nonempty intersection with both
![]() $V(\mathcal {G})$
and
$V(\mathcal {G})$
and
![]() $V(\mathcal {H})$
. For simplicity, we define the join of an r-graph
$V(\mathcal {H})$
. For simplicity, we define the join of an r-graph
![]() $\mathcal {H}$
and a family
$\mathcal {H}$
and a family
![]() $\mathcal {F}$
of r-graphs as
$\mathcal {F}$
of r-graphs as ![]() .
.
Erdős [Reference Erdős13] considered the density problem for
![]() $K_3$
and proved the following result.
$K_3$
and proved the following result.
Theorem 1.3 (Erdős [Reference Erdős13])
Suppose that
![]() $n, t\in \mathbb {N}$
and
$n, t\in \mathbb {N}$
and
![]() $t\le \sqrt {n/400}$
. Then
$t\le \sqrt {n/400}$
. Then
Later, Moon [Reference Moon58] extended it to all complete graphs.
Theorem 1.4 (Moon [Reference Moon58])
Suppose that integers
![]() $n, t, \ell \in \mathbb {N}$
satisfy
$n, t, \ell \in \mathbb {N}$
satisfy
![]() $\ell \ge 2$
,
$\ell \ge 2$
,
![]() $t\le \frac {2n-3\ell ^2+2\ell }{\ell ^3+2\ell ^2+\ell +1}$
, and
$t\le \frac {2n-3\ell ^2+2\ell }{\ell ^3+2\ell ^2+\ell +1}$
, and
![]() $\ell \mid (n-t)$
. Then
$\ell \mid (n-t)$
. Then
It is worth mentioning that, in fact, for
![]() $\ell = 2$
, Moon proved that the constraint
$\ell = 2$
, Moon proved that the constraint
![]() $\ell \mid (n-t)$
can be removed, and moreover, (1.1) holds for all
$\ell \mid (n-t)$
can be removed, and moreover, (1.1) holds for all
![]() $t \le \frac {2n-8}{9}$
. For
$t \le \frac {2n-8}{9}$
. For
![]() $\ell \ge 3$
, Moon remarked in [Reference Moon58] that there are some difficulties to remove the constraint
$\ell \ge 3$
, Moon remarked in [Reference Moon58] that there are some difficulties to remove the constraint
![]() $\ell \mid (n-t)$
. Nevertheless, the divisibility constraint is not required in our results. Meanwhile, Simonovits [Reference Simonovits76] also considered this problem and proved that if
$\ell \mid (n-t)$
. Nevertheless, the divisibility constraint is not required in our results. Meanwhile, Simonovits [Reference Simonovits76] also considered this problem and proved that if
![]() $t\ge 1$
and
$t\ge 1$
and
![]() $\ell \ge 2$
are fixed integers, then (1.1) holds for all sufficiently large n.
$\ell \ge 2$
are fixed integers, then (1.1) holds for all sufficiently large n.
It becomes much more complicated when extending Theorem 1.4 to larger t. Indeed, a full density version of the Corrádi–Hajnal theorem was obtained only very recently by Allen, Böttcher, Hladký, and Piguet [Reference Allen, Böttcher, Hladký and Piguet2] for large n. Their results show that, interestingly, there are four different extremal constructions for four different regimes of t, and the construction ![]() is extremal only for
is extremal only for
![]() $t \le \frac {2n-6}{9}$
. For the other three extremal constructions, we refer the reader to their paper for details. For larger complete graphs, it seems that there are even no conjectures for the extremal constructions in general (see remarks in the last section of [Reference Allen, Böttcher, Hladký and Piguet2]).
$t \le \frac {2n-6}{9}$
. For the other three extremal constructions, we refer the reader to their paper for details. For larger complete graphs, it seems that there are even no conjectures for the extremal constructions in general (see remarks in the last section of [Reference Allen, Böttcher, Hladký and Piguet2]).
The objective of this work is to provide a general approach to determine
![]() $\mathrm {ex}(n, (t+1)F)$
for nondegenerate hypergraphs (including graphs) F when n is sufficiently large and t is within the range of
$\mathrm {ex}(n, (t+1)F)$
for nondegenerate hypergraphs (including graphs) F when n is sufficiently large and t is within the range of
![]() $[0, c_F n]$
, where
$[0, c_F n]$
, where
![]() $c_F>0$
is a small constant depending only on F. It is worth mentioning that general methods of this nature are rare for hypergraph Turán-type problems, with only a few notable recent instances, as exemplified by [Reference Brandt, Irwin and Jiang9, Reference Liu, Mubayi and Reiher51, Reference Norin and Yepremyan65]. Our main results are stated in the next section after the introduction of some necessary definitions. We hope our results could shed some light on a full generalization of the density version of the Corrádi–Hajnal and Hajnal–Szemerédi theorems.
$c_F>0$
is a small constant depending only on F. It is worth mentioning that general methods of this nature are rare for hypergraph Turán-type problems, with only a few notable recent instances, as exemplified by [Reference Brandt, Irwin and Jiang9, Reference Liu, Mubayi and Reiher51, Reference Norin and Yepremyan65]. Our main results are stated in the next section after the introduction of some necessary definitions. We hope our results could shed some light on a full generalization of the density version of the Corrádi–Hajnal and Hajnal–Szemerédi theorems.
1.2 Main results
Given an r-graph F and an integer
![]() $n \in \mathbb {N}$
define
$n \in \mathbb {N}$
define
Observe that
![]() $d(n,F)$
is the average degree of hypergraphs in
$d(n,F)$
is the average degree of hypergraphs in
![]() $\mathrm {EX}(n,F)$
, and
$\mathrm {EX}(n,F)$
, and
![]() $\delta (n,F)$
is a lower bound for the minimum degree of hypergraphs in
$\delta (n,F)$
is a lower bound for the minimum degree of hypergraphs in
![]() $\mathrm {EX}(n,F)$
(see Fact 4.1).
$\mathrm {EX}(n,F)$
(see Fact 4.1).
The following two definitions are crucial for our main results. The first definition concerns the maximum degree of a near-extremal F-free r-graph.
Definition 1.1 (Boundedness)
Let
![]() $f_1, f_2 \colon \mathbb {N} \to \mathbb {R}$
be two nonnegative functions. An r-graph F is
$f_1, f_2 \colon \mathbb {N} \to \mathbb {R}$
be two nonnegative functions. An r-graph F is
![]() $\left (f_1, f_2\right )$
-bounded if every F-free r-graph
$\left (f_1, f_2\right )$
-bounded if every F-free r-graph
![]() $\mathcal {H}$
on n vertices with average degree at least
$\mathcal {H}$
on n vertices with average degree at least
![]() $d(n, F) - f_1(n)$
satisfies
$d(n, F) - f_1(n)$
satisfies
![]() $\Delta (\mathcal {H}) \le d(n, F) + f_2(n)$
, i.e.,
$\Delta (\mathcal {H}) \le d(n, F) + f_2(n)$
, i.e.,
Remark For our purposes, it suffices to take
![]() $f_1(n) = \varepsilon n^{r-1}$
and
$f_1(n) = \varepsilon n^{r-1}$
and
![]() $f_2(n) = \delta n^{r-1}$
for some small constants
$f_2(n) = \delta n^{r-1}$
for some small constants
![]() $\varepsilon , \delta>0$
.
$\varepsilon , \delta>0$
.
Later we will prove that families with certain stability properties also have good boundedness (see Theorem 1.9).
The next definition concerns the smoothness of the Turán function
![]() $\mathrm {ex}(n,F)$
.
$\mathrm {ex}(n,F)$
.
Definition 1.2 (Smoothness)
Let
![]() $g \colon \mathbb {N} \to \mathbb {R}$
be a nonnegative function. The Turán function
$g \colon \mathbb {N} \to \mathbb {R}$
be a nonnegative function. The Turán function
![]() $\mathrm {ex}(n, F)$
of an r-graph F is g-smooth if
$\mathrm {ex}(n, F)$
of an r-graph F is g-smooth if
Remark Similarly, for our results, it suffices to take
![]() $g(n) = \gamma n^{r-1}$
for some small constant
$g(n) = \gamma n^{r-1}$
for some small constant
![]() $\gamma> 0$
.
$\gamma> 0$
.
Assumptions on the smoothness of
![]() $\mathrm {ex}(n, F)$
were used by several researchers before. See, for example, [Reference Allen, Keevash, Sudakov and Verstraëte3, Reference Jiang, Longbrake and Ma39] for degenerate graphs and see, for example, [Reference Keevash, Lenz and Mubayi43, Theorem 1.4] for nondegenerate hypergraphs.
$\mathrm {ex}(n, F)$
were used by several researchers before. See, for example, [Reference Allen, Keevash, Sudakov and Verstraëte3, Reference Jiang, Longbrake and Ma39] for degenerate graphs and see, for example, [Reference Keevash, Lenz and Mubayi43, Theorem 1.4] for nondegenerate hypergraphs.
Now we are ready to state our main result.
Theorem 1.5 Fix integers
![]() $m \ge r \ge 2$
and a nondegenerate r-graph F on m vertices. Suppose that there exists a constant
$m \ge r \ge 2$
and a nondegenerate r-graph F on m vertices. Suppose that there exists a constant
![]() $c>0$
such that for all sufficiently large
$c>0$
such that for all sufficiently large
![]() $n\in \mathbb {N} \colon $
$n\in \mathbb {N} \colon $
-
(a) F is
 $\left (c\binom {n}{r-1}, \frac {1-\pi (F)}{4m}\binom {n}{r-1}\right )$
-bounded, and
$\left (c\binom {n}{r-1}, \frac {1-\pi (F)}{4m}\binom {n}{r-1}\right )$
-bounded, and -
(b)
 $\mathrm {ex}(n, F)$
is
$\mathrm {ex}(n, F)$
is
 $\frac {1-\pi (F)}{8m}\binom {n}{r-1}$
-smooth.
$\frac {1-\pi (F)}{8m}\binom {n}{r-1}$
-smooth.
Then there exists
![]() $N_0$
such that for all integers
$N_0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t \le \min \left \{\frac {c}{4erm}n, \frac {1-\pi (F)}{64rm^2}n\right \}$
, we have
$t \le \min \left \{\frac {c}{4erm}n, \frac {1-\pi (F)}{64rm^2}n\right \}$
, we have
and, in particular,
Remarks
-
• Assumption (a) cannot be removed, as demonstrated by the following example
 $\colon $
let
$\colon $
let
 $F = 2K_3$
and let
$F = 2K_3$
and let
 $t \ge 2$
, then A less obvious example is the triangle-blowup of cycles, which can be deduced similarly from the results in recent work [Reference Liu, Song and Yuan54, Theorem 1.9].
$t \ge 2$
, then A less obvious example is the triangle-blowup of cycles, which can be deduced similarly from the results in recent work [Reference Liu, Song and Yuan54, Theorem 1.9]. $$ \begin{align*} \mathrm{ex}(n,(t+1)F) = \mathrm{ex}(n,(2t+2)K_3) & \ge \binom{n}{2}-\binom{n-2t-1}{2}+ \left\lfloor \frac{(n-2t-1)^2}{4} \right\rfloor \\ &> \binom{n}{2}-\binom{n-t}{2} + \left\lfloor \frac{(n-1)^2}{4} \right\rfloor + n-1 \\ & = \binom{n}{2}-\binom{n-t}{2} + \mathrm{ex}(n-t, F). \end{align*} $$
$$ \begin{align*} \mathrm{ex}(n,(t+1)F) = \mathrm{ex}(n,(2t+2)K_3) & \ge \binom{n}{2}-\binom{n-2t-1}{2}+ \left\lfloor \frac{(n-2t-1)^2}{4} \right\rfloor \\ &> \binom{n}{2}-\binom{n-t}{2} + \left\lfloor \frac{(n-1)^2}{4} \right\rfloor + n-1 \\ & = \binom{n}{2}-\binom{n-t}{2} + \mathrm{ex}(n-t, F). \end{align*} $$
-
• Assumption (b) can probably be omitted, as it was conjecturedFootnote 1 that every F is
 $o(n^{r-1})$
-smooth and this is true for
$o(n^{r-1})$
-smooth and this is true for
 $r=2$
by a classic result of Simonovits (see [Reference Simonovits76, p. 317]).
$r=2$
by a classic result of Simonovits (see [Reference Simonovits76, p. 317]).
Fix an r-graph F on m vertices. We say a collection
![]() $\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
of r-graphs on the same vertex set V has a rainbow F-matching if there exists a collection
$\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
of r-graphs on the same vertex set V has a rainbow F-matching if there exists a collection
![]() $\left \{S_i \colon i \in [t+1]\right \}$
of pairwise disjoint m-subsets of V such that
$\left \{S_i \colon i \in [t+1]\right \}$
of pairwise disjoint m-subsets of V such that
![]() $F \subset \mathcal {H}_{i}[S_i]$
for all
$F \subset \mathcal {H}_{i}[S_i]$
for all
![]() ${i\in [t+1]}$
.
${i\in [t+1]}$
.
Recently, there has been considerable interest in extending some classical results to a rainbow version. See, for example, [Reference Aharoni and Howard1, Reference Gao, Lu, Ma and Yu31, Reference Huang, Loh and Sudakov38, Reference Kiselev and Kupavskii47, Reference Lu, Wang and Yu55, Reference Lu, Wang and Yu56] for some recent progress on the rainbow version of the Erdős Matching conjecture. Here, we include the following rainbow version of Theorem 1.5.
Theorem 1.6 The following holds under the assumption of Theorem 1.5. If a collection
![]() $\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
of n-vertex r-graphs on the same vertex set satisfies
$\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
of n-vertex r-graphs on the same vertex set satisfies
then
![]() $\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
contains a rainbow F-matching.
$\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
contains a rainbow F-matching.
Observe that (1.3) follows immediately by letting
![]() $\mathcal {H}_1 = \cdots = \mathcal {H}_{t+1}$
in Theorem 1.6. In fact, we will prove Theorem 1.6 first (which yields (1.3)), and then we prove (1.2) by adding some further argument.
$\mathcal {H}_1 = \cdots = \mathcal {H}_{t+1}$
in Theorem 1.6. In fact, we will prove Theorem 1.6 first (which yields (1.3)), and then we prove (1.2) by adding some further argument.
1.3 Boundedness and smoothness
In this subsection, we present some simple sufficient conditions for an r-graph to have good boundedness and smoothness. Before stating our results, let us introduce some necessary definitions.
For most nondegenerate Turán problems where the exact value of the Turán number is known, the extremal constructions have simple structures. We use the following notions to encode the structural information of a hypergraph.
Let an r-multiset mean an unordered collection of r elements with repetitions allowed. Let E be a collection of r-multisets on
![]() $[k]$
. Let
$[k]$
. Let
![]() $V_1,\dots ,V_k$
be disjoint sets and let
$V_1,\dots ,V_k$
be disjoint sets and let
![]() $V:=V_1\cup \dots \cup V_k$
. The profile of an r-set
$V:=V_1\cup \dots \cup V_k$
. The profile of an r-set
![]() $X\subseteq V$
(with respect to
$X\subseteq V$
(with respect to
![]() $V_1,\dots ,V_k$
) is the r-multiset on
$V_1,\dots ,V_k$
) is the r-multiset on
![]() $[k]$
that contains
$[k]$
that contains
![]() $i\in [k]$
with multiplicity
$i\in [k]$
with multiplicity
![]() $|X\cap V_i|$
. For an r-multiset
$|X\cap V_i|$
. For an r-multiset
![]() $Y\subseteq [k]$
, let
$Y\subseteq [k]$
, let
![]() $Y(\!(V_1,\dots ,V_k)\!)$
consist of all r-subsets of V whose profile is Y. The r-graph
$Y(\!(V_1,\dots ,V_k)\!)$
consist of all r-subsets of V whose profile is Y. The r-graph
![]() $Y(\!(V_1,\dots ,V_k)\!)$
is called the blowup of Y (with respect to
$Y(\!(V_1,\dots ,V_k)\!)$
is called the blowup of Y (with respect to
![]() $V_1,\dots ,V_k$
) and the r-graph
$V_1,\dots ,V_k$
) and the r-graph
is called the blowup of E (with respect to
![]() $V_1,\dots ,V_k$
).
$V_1,\dots ,V_k$
).
An (r-uniform) pattern is a pair
![]() $P=(k,E)$
where k is a positive integer and E is a collection of r-multisets on
$P=(k,E)$
where k is a positive integer and E is a collection of r-multisets on
![]() $[k]$
. It is clear that pattern is a generalization of r-graphs, since an r-graph is a pattern in which E consists of only simple r-sets. If it is clear from the context, we will use E to represent the pattern P for simplicity (like what we did for hypergraphs). Moreover, if E consists of a single element, we will use this element to represent E.
$[k]$
. It is clear that pattern is a generalization of r-graphs, since an r-graph is a pattern in which E consists of only simple r-sets. If it is clear from the context, we will use E to represent the pattern P for simplicity (like what we did for hypergraphs). Moreover, if E consists of a single element, we will use this element to represent E.
We say an r-graph
![]() $\mathcal {G}$
is a P-construction on a set V if there exists a partition
$\mathcal {G}$
is a P-construction on a set V if there exists a partition
![]() $V = V_1 \cup \cdots \cup V_{k}$
such that
$V = V_1 \cup \cdots \cup V_{k}$
such that
![]() $\mathcal {G} = E(\!(V_1,\dots ,V_k)\!)$
. An r-graph
$\mathcal {G} = E(\!(V_1,\dots ,V_k)\!)$
. An r-graph
![]() $\mathcal {H}$
is a P-subconstruction if it is a subgraph of some P-construction. For example, the Turán graph
$\mathcal {H}$
is a P-subconstruction if it is a subgraph of some P-construction. For example, the Turán graph
![]() $T(n,\ell )$
is a
$T(n,\ell )$
is a
![]() $K_{\ell }$
-construction on
$K_{\ell }$
-construction on
![]() $[n]$
, and an
$[n]$
, and an
![]() $\ell $
-partite graph is a
$\ell $
-partite graph is a
![]() $K_{\ell }$
-subconstruction.
$K_{\ell }$
-subconstruction.
Let
![]() $\Lambda (P, n)$
denote the maximum number of edges in a P-construction with n vertices and define the Lagrangian of P as the limit
$\Lambda (P, n)$
denote the maximum number of edges in a P-construction with n vertices and define the Lagrangian of P as the limit
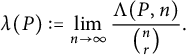 $$ \begin{align*} \lambda(P) := \lim_{n\to \infty} \frac{\Lambda(P, n)}{\binom{n}{r}}. \end{align*} $$
$$ \begin{align*} \lambda(P) := \lim_{n\to \infty} \frac{\Lambda(P, n)}{\binom{n}{r}}. \end{align*} $$
Using a simple averaging argument, one can show that
![]() ${\Lambda (P, n)}/{\binom {n}{r}}$
is nonincreasing, and hence, the limit exists (see [Reference Pikhurko69, Lemma 10]). We say a pattern
${\Lambda (P, n)}/{\binom {n}{r}}$
is nonincreasing, and hence, the limit exists (see [Reference Pikhurko69, Lemma 10]). We say a pattern
![]() $P = (k,E)$
is minimum if
$P = (k,E)$
is minimum if
![]() $\lambda (P-i) < \lambda (P)$
for all
$\lambda (P-i) < \lambda (P)$
for all
![]() $i\in [k]$
, where
$i\in [k]$
, where
![]() $P-i$
denotes the new pattern obtained from P by removing i from
$P-i$
denotes the new pattern obtained from P by removing i from
![]() $[k]$
and removing all r-multisets containing i from E. Note that the Lagrangian of a pattern is a generalization of the well-known hypergraph Lagrangian (see, e.g., [Reference Baber and Talbot5, Reference Frankl and Rödl26]) that has been successfully applied to Turán-type problems, with the basic idea going back to Motzkin and Straus [Reference Motzkin and Straus59].
$[k]$
and removing all r-multisets containing i from E. Note that the Lagrangian of a pattern is a generalization of the well-known hypergraph Lagrangian (see, e.g., [Reference Baber and Talbot5, Reference Frankl and Rödl26]) that has been successfully applied to Turán-type problems, with the basic idea going back to Motzkin and Straus [Reference Motzkin and Straus59].
Remark The notion of pattern was introduced by Pikhurko in [Reference Pikhurko69] to study the general properties of nondegenerate hypergraph Turán problems, and it was also used very recently in [Reference Liu and Pikhurko52, Reference Liu and Pikhurko53]. Note that the definition of pattern in [Reference Pikhurko69] is more general by allowing recursive parts. Our results about patterns in this work can be easily extended to this more general setting.
Let F be an r-graph and P be a pattern. We say
![]() $(F,P)$
is a Turán pair if every P-construction is F-free and every maximum F-free construction is a P-construction. For example, it follows from the Turán theorem that
$(F,P)$
is a Turán pair if every P-construction is F-free and every maximum F-free construction is a P-construction. For example, it follows from the Turán theorem that
![]() $\left (K_{\ell +1}, K_{\ell }\right )$
is a Turán pair for all
$\left (K_{\ell +1}, K_{\ell }\right )$
is a Turán pair for all
![]() $\ell \ge 2$
. It is easy to observe that for a Turán pair
$\ell \ge 2$
. It is easy to observe that for a Turán pair
![]() $(F,P)$
, we have
$(F,P)$
, we have
For hypergraphs in Turán pairs, we have the following result concerning the smoothness of their Turán functions.
Theorem 1.7 Suppose that F is an r-graph and P is a minimal pattern such that
![]() $(F,P)$
is a Turán pair. Then
$(F,P)$
is a Turán pair. Then
![]() $\mathrm {ex}(n, F)$
is
$\mathrm {ex}(n, F)$
is
![]() $4\binom {n-1}{r-2}$
-smooth.
$4\binom {n-1}{r-2}$
-smooth.
The boundedness of F is closely related to the stability of F. So we introduce some definitions related to stability. Suppose that
![]() $(F,P)$
is a Turán pair.
$(F,P)$
is a Turán pair.
-
• We say F is edge-stable with respect to P if for every
 $\delta>0$
there exist constants
$\delta>0$
there exist constants
 $N_0$
and
$N_0$
and
 $\zeta>0$
such that for every F-free r-graph
$\zeta>0$
such that for every F-free r-graph
 $\mathcal {H}$
on
$\mathcal {H}$
on
 $n \ge N_0$
vertices with at least
$n \ge N_0$
vertices with at least
 $\left (\pi (F)-\zeta \right )\binom {n}{r}$
edges, there exists a subgraph
$\left (\pi (F)-\zeta \right )\binom {n}{r}$
edges, there exists a subgraph
 $\mathcal {H}^{\prime }\subset \mathcal {H}$
with at least
$\mathcal {H}^{\prime }\subset \mathcal {H}$
with at least
 $\left (\pi (F)-\delta \right )\binom {n}{r}$
edges such that
$\left (\pi (F)-\delta \right )\binom {n}{r}$
edges such that
 $\mathcal {H}^{\prime }$
is a P-subconstruction.
$\mathcal {H}^{\prime }$
is a P-subconstruction. -
• We say F is vertex-extendable with respect to P if there exist constants
 $N_0$
and
$N_0$
and
 $\zeta>0$
such that for every F-free r-graph
$\zeta>0$
such that for every F-free r-graph
 $\mathcal {H}$
on
$\mathcal {H}$
on
 $n \ge N_0$
vertices satisfing
$n \ge N_0$
vertices satisfing
 $\delta (\mathcal {H}) \ge \left (\pi (F)-\zeta \right )\binom {n-1}{r-1}$
the following holds: if
$\delta (\mathcal {H}) \ge \left (\pi (F)-\zeta \right )\binom {n-1}{r-1}$
the following holds: if
 $\mathcal {H}-v$
is a P-subconstruction for some vertex
$\mathcal {H}-v$
is a P-subconstruction for some vertex
 $v\in V(\mathcal {H})$
, then
$v\in V(\mathcal {H})$
, then
 $\mathcal {H}$
is also a P-subconstruction.
$\mathcal {H}$
is also a P-subconstruction. -
• We say F is weakly vertex-extendable with respect to P if for every
 $\delta>0$
there exist constants
$\delta>0$
there exist constants
 $N_0$
and
$N_0$
and
 $\zeta>0$
such that for every F-free r-graph
$\zeta>0$
such that for every F-free r-graph
 $\mathcal {H}$
on
$\mathcal {H}$
on
 $n \ge N_0$
vertices satisfying
$n \ge N_0$
vertices satisfying
 $\delta (\mathcal {H}) \ge \left (\pi (F)-\zeta \right )\binom {n-1}{r-1}$
the following holds: if
$\delta (\mathcal {H}) \ge \left (\pi (F)-\zeta \right )\binom {n-1}{r-1}$
the following holds: if
 $\mathcal {H}-v$
is a P-subconstruction for some vertex
$\mathcal {H}-v$
is a P-subconstruction for some vertex
 $v\in V(\mathcal {H})$
, then
$v\in V(\mathcal {H})$
, then
 $d_{\mathcal {H}}(v) \le \left (\pi (F)+\delta \right )\binom {n-1}{r-1}$
.
$d_{\mathcal {H}}(v) \le \left (\pi (F)+\delta \right )\binom {n-1}{r-1}$
.
For simplicity, if P is clear from the context, we will simply say that F is edge-stable, vertex-extendable, and weakly vertex-extendable, respectively.
The first stability theorem which states that
![]() $K_{\ell +1}$
is edge-stable with respect to
$K_{\ell +1}$
is edge-stable with respect to
![]() $K_{\ell }$
was proved independently by Erdős and Simonovits [Reference Simonovits76], and it was used first by Simonovits [Reference Simonovits76] to determine the exact Turán number
$K_{\ell }$
was proved independently by Erdős and Simonovits [Reference Simonovits76], and it was used first by Simonovits [Reference Simonovits76] to determine the exact Turán number
![]() $\mathrm {ex}(n,F)$
of an edge-critical graph F for large n. Later, Simonovits’ method (also known as the Stability Method) was used by many researchers to determine the Turán numbers of a large collection of hypergraphs (see Section 2 for more details).
$\mathrm {ex}(n,F)$
of an edge-critical graph F for large n. Later, Simonovits’ method (also known as the Stability Method) was used by many researchers to determine the Turán numbers of a large collection of hypergraphs (see Section 2 for more details).
The definition of vertex-extendability was introduced by Mubayi, Reiher, and the third author in [Reference Liu, Mubayi and Reiher51] for a unified framework for proving the stability of a large class of hypergraphs.
The definition of weak vertex-extendability seems to be new, and it is clear from (1.4) and the following lemma that for a Turán pair
![]() $(F,P)$
the vertex-extendability implies the weak vertex-extendability. There are several examples showing that the inverse is not true in general (see, e.g., Section 2.6). It seems interesting to explore the relations between the weak vertex-extendability and other types of stability (see [Reference Liu, Mubayi and Reiher51] for more details).
$(F,P)$
the vertex-extendability implies the weak vertex-extendability. There are several examples showing that the inverse is not true in general (see, e.g., Section 2.6). It seems interesting to explore the relations between the weak vertex-extendability and other types of stability (see [Reference Liu, Mubayi and Reiher51] for more details).
Lemma 1.8 [Reference Liu and Pikhurko52, Lemma 21]
Suppose that P is a minimal pattern. Then for every
![]() $\delta>0$
there exist
$\delta>0$
there exist
![]() $N_0$
and
$N_0$
and
![]() $\varepsilon>0$
such that every P-subconstruction
$\varepsilon>0$
such that every P-subconstruction
![]() $\mathcal {H}$
on
$\mathcal {H}$
on
![]() $n \ge N_0$
vertices with
$n \ge N_0$
vertices with
![]() $\delta (\mathcal {H}) \ge \left (\lambda (P)-\varepsilon \right )\binom {n-1}{r-1}$
satisfies
$\delta (\mathcal {H}) \ge \left (\lambda (P)-\varepsilon \right )\binom {n-1}{r-1}$
satisfies
![]() $\Delta (\mathcal {H}) \le \left (\lambda (P)+ \delta \right )\binom {n-1}{r-1}$
.
$\Delta (\mathcal {H}) \le \left (\lambda (P)+ \delta \right )\binom {n-1}{r-1}$
.
Let us add another remark about the weak vertex-extendability that might be useful for readers who are familiar with the stability method. In a standard stability argument in determining the exact value of
![]() $\mathrm {ex}(n,F)$
, one usually defines a set
$\mathrm {ex}(n,F)$
, one usually defines a set
![]() $\mathcal {B}$
of bad edges and a set
$\mathcal {B}$
of bad edges and a set
![]() $\mathcal {M}$
of missing edges, and then tries to prove that
$\mathcal {M}$
of missing edges, and then tries to prove that
![]() $|\mathcal {M}|> |\mathcal {B}|$
. One key step in this argument is to prove that the maximum degree of
$|\mathcal {M}|> |\mathcal {B}|$
. One key step in this argument is to prove that the maximum degree of
![]() $\mathcal {B}$
is small (more specifically,
$\mathcal {B}$
is small (more specifically,
![]() $\Delta (B) = o(n^{r-1})$
), which, informally speaking, usually implies the weak vertex-extendability of F.
$\Delta (B) = o(n^{r-1})$
), which, informally speaking, usually implies the weak vertex-extendability of F.
For a Turán pair
![]() $(F,P)$
with the weak vertex-extendability, we have the following result concerning the boundedness of F.
$(F,P)$
with the weak vertex-extendability, we have the following result concerning the boundedness of F.
Theorem 1.9 Suppose that F is an r-graph and P is a minimal pattern such that F is edge-stable and weakly vertex-extendable (or vertex-extendable) with respect to P. Then there exists a constant
![]() $c>0$
such that F is
$c>0$
such that F is
![]() $\left (c \binom {n-1}{r-1}, \frac {1-\pi (F)}{8m} \binom {n-1}{r-1}\right )$
-bounded for large n.
$\left (c \binom {n-1}{r-1}, \frac {1-\pi (F)}{8m} \binom {n-1}{r-1}\right )$
-bounded for large n.
Remark It seems possible to extend Theorems 1.7 and 1.9 to nonminimal patterns, but we do not aware of any r-graph F whose extremal construction is a P-construction for some nonminimal pattern P. However, there does exist a finite family
![]() $\mathcal {F}$
of r-graphs whose extremal construction is a P-construction for some nonminimal pattern P (see [Reference Hou, Li, Liu, Mubayi and Zhang37] for more details).
$\mathcal {F}$
of r-graphs whose extremal construction is a P-construction for some nonminimal pattern P (see [Reference Hou, Li, Liu, Mubayi and Zhang37] for more details).
In many cases, (weak) vertex-extendability of F follows from a stronger type of stability that was studied by many researchers before. Suppose that
![]() $(F,P)$
is a Turán pair. We say F is degree-stable with respect to P if there exists
$(F,P)$
is a Turán pair. We say F is degree-stable with respect to P if there exists
![]() $\zeta>0$
such that for large n every n-vertex F-free r-graph
$\zeta>0$
such that for large n every n-vertex F-free r-graph
![]() $\mathcal {H}$
with
$\mathcal {H}$
with
![]() $\delta (\mathcal {H}) \ge \left (\pi (F) - \zeta \right ) \binom {n-1}{r-1}$
is a P-subconstruction. It is easy to observe from the definition that if F is degree-stable with respect to P, then F is edge-stable and vertex-extendable with respect to P. Therefore, we have the following corollary of Theorems 1.7 and 1.9.
$\delta (\mathcal {H}) \ge \left (\pi (F) - \zeta \right ) \binom {n-1}{r-1}$
is a P-subconstruction. It is easy to observe from the definition that if F is degree-stable with respect to P, then F is edge-stable and vertex-extendable with respect to P. Therefore, we have the following corollary of Theorems 1.7 and 1.9.
Corollary 1.10 Suppose that F is an r-graph and P is a minimal pattern such that F is degree-stable with respect to P. Then there exists a constant
![]() $c>0$
such that
$c>0$
such that
-
(a)
 $\mathrm {ex}(n,F)$
is
$\mathrm {ex}(n,F)$
is
 $4\binom {n-1}{r-2}$
-smooth, and
$4\binom {n-1}{r-2}$
-smooth, and -
(b) F is
 $\left (c \binom {n-1}{r-1}, \frac {1-\pi (F)}{8m} \binom {n-1}{r-1}\right )$
-bounded.
$\left (c \binom {n-1}{r-1}, \frac {1-\pi (F)}{8m} \binom {n-1}{r-1}\right )$
-bounded.
In the next section, we show some applications of Theorems 1.5, 1.7, and 1.9, and Corollary 1.10. We omit the applications of Theorem 1.6 since they are quite straightforward to obtain once we present the corresponding applications of Theorem 1.5. The proofs for Theorems 1.5 and 1.6 are included in Section 3. The proofs for Theorems 1.7 and 1.9 are included in Section 4.
2 Applications
Combining some known stability results with Theorems 1.5, 1.7, and 1.9 (or Corollary 1.10) we can immediately obtain results in this section. To demonstrate a way to apply Theorems 1.5, 1.7, and 1.9 in general, we include the short proof for the weak vertex-extendability of
![]() $\mathbb {F}_{3,2}$
as defined in Section 2.7 (even though it can be deduced from results in [Reference Füredi, Pikhurko and Simonovits28]).
$\mathbb {F}_{3,2}$
as defined in Section 2.7 (even though it can be deduced from results in [Reference Füredi, Pikhurko and Simonovits28]).
2.1 Edge-critical graphs
Recall that for a graph F its chromatic number is denoted by
![]() $\chi (F)$
. We say a graph F is edge-critical if there exists an edge
$\chi (F)$
. We say a graph F is edge-critical if there exists an edge
![]() $e\in F$
such that
$e\in F$
such that
![]() $\chi (F-e) < \chi (F)$
. Using the stability method, Simonovits proved in [Reference Simonovits76] that if a graph F is edge-critical and
$\chi (F-e) < \chi (F)$
. Using the stability method, Simonovits proved in [Reference Simonovits76] that if a graph F is edge-critical and
![]() $\chi (F) \ge 3$
, then
$\chi (F) \ge 3$
, then
![]() $\mathrm {EX}(n,F) = \{T(n, \chi (F)-1)\}$
for all sufficiently large n.
$\mathrm {EX}(n,F) = \{T(n, \chi (F)-1)\}$
for all sufficiently large n.
Extending the classical Andrásfai–Erdős–Sós theorem [Reference Andrásfai, Erdős and Sós4], Erdős and Simonovits [Reference Erdős and Simonovits17] proved that every edge-critical graph with chromatic number at least
![]() $3$
is degree-stable. Therefore, combined with Theorem 1.5 and Corollary 1.10, we obtain the following result.
$3$
is degree-stable. Therefore, combined with Theorem 1.5 and Corollary 1.10, we obtain the following result.
Theorem 2.1 Suppose that F is an edge-critical graph with
![]() $\chi (F) \ge 3$
. Then there exist constants
$\chi (F) \ge 3$
. Then there exist constants
![]() $N_0$
and
$N_0$
and
![]() $c_F>0$
such that for all integers
$c_F>0$
such that for all integers
![]() $n\ge N_0$
and
$n\ge N_0$
and
![]() $t \in [0, c_F n]$
we have
$t \in [0, c_F n]$
we have
Remarks
-
• For Theorem 2.1 and all other theorems in this section, we did not try to optimize the constant
 $c_F$
, but it seems possible to obtain a reasonable boundFootnote
2
for
$c_F$
, but it seems possible to obtain a reasonable boundFootnote
2
for
 $c_F$
by a more careful analysis of the proof for Theorem 1.9 (and the proof for the (weak) vertex-extendability of F in some cases).
$c_F$
by a more careful analysis of the proof for Theorem 1.9 (and the proof for the (weak) vertex-extendability of F in some cases). -
• The case when F is an odd cycle was also considered in a recent paper [Reference Fang, Zhai and Lin19, Theorem 1.1].
-
• It might be true that Theorem 2.1 holds for a broader class of graphs, and it would be interesting to characterize the class of graphs for which Theorem 2.1 holds.
2.2 The Fano plane
The Fano plane
![]() $\mathbb {F}$
is a
$\mathbb {F}$
is a
![]() $3$
-graph with vertex set
$3$
-graph with vertex set
![]() $\{1,2,3,4,5,6,7\}$
and edge set
$\{1,2,3,4,5,6,7\}$
and edge set
Let
![]() $[n] = V_1 \cup V_2$
be a partition with
$[n] = V_1 \cup V_2$
be a partition with
![]() $|V_1| = \lfloor n/2 \rfloor $
and
$|V_1| = \lfloor n/2 \rfloor $
and
![]() $|V_2| = \lceil n/2 \rceil $
. Let
$|V_2| = \lceil n/2 \rceil $
. Let
![]() $B_3(n)$
denote the
$B_3(n)$
denote the
![]() $3$
-graph on
$3$
-graph on
![]() $[n]$
whose edge set consists of all triples that have a nonempty intersection with both
$[n]$
whose edge set consists of all triples that have a nonempty intersection with both
![]() $V_1$
and
$V_1$
and
![]() $V_2$
(see Figure 1). Note that
$V_2$
(see Figure 1). Note that
![]() $|B_3(n)| \sim \frac {3}{4}\binom {n}{3}$
.
$|B_3(n)| \sim \frac {3}{4}\binom {n}{3}$
.

Figure 1: The Fano plane and the complete bipartite
![]() $3$
-graph
$3$
-graph
![]() $B_3(n)$
.
$B_3(n)$
.
It was conjectured by Sós [Reference Sós77] and famously proved by De Caen and Füredi [Reference De Caen and Füredi11] that
![]() $\pi (\mathbb {F}) = 3/4$
. Later, using a stability argument, Keevash and Sudakov [Reference Keevash and Sudakov46], and independently, Füredi and Simonovits [Reference Füredi and Simonovits30] proved that
$\pi (\mathbb {F}) = 3/4$
. Later, using a stability argument, Keevash and Sudakov [Reference Keevash and Sudakov46], and independently, Füredi and Simonovits [Reference Füredi and Simonovits30] proved that
![]() $\mathrm {EX}(n, \mathbb {F}) = \{B_3(n)\}$
for all sufficienly large n. Recently, Bellmann and Reiher [Reference Bellmann and Reiher6] proved that
$\mathrm {EX}(n, \mathbb {F}) = \{B_3(n)\}$
for all sufficienly large n. Recently, Bellmann and Reiher [Reference Bellmann and Reiher6] proved that
![]() $\mathrm {ex}(n, \mathbb {F}) = |B_3(n)| = \frac {n-2}{2}\lfloor \frac {n^2}{4}\rfloor $
for all
$\mathrm {ex}(n, \mathbb {F}) = |B_3(n)| = \frac {n-2}{2}\lfloor \frac {n^2}{4}\rfloor $
for all
![]() $n \ge 7$
, and moreover, they proved that
$n \ge 7$
, and moreover, they proved that
![]() $B_3(n)$
is the unique extremal construction for all
$B_3(n)$
is the unique extremal construction for all
![]() $n \ge 8$
.
$n \ge 8$
.
It follows from the result of Keevash and Sudakov [Reference Keevash and Sudakov46], and independently, Füredi and Simonovits [Reference Füredi and Simonovits30] that
![]() $\mathbb {F}$
is degree-stable. Therefore, we obtain the following result.
$\mathbb {F}$
is degree-stable. Therefore, we obtain the following result.
Theorem 2.2 There exist constants
![]() $N_0$
and
$N_0$
and
![]() $c_{\mathbb {F}}>0$
such that for all integers
$c_{\mathbb {F}}>0$
such that for all integers
![]() $n\ge N_0$
and
$n\ge N_0$
and
![]() $t \in [0, c_{\mathbb {F}} n]$
we have
$t \in [0, c_{\mathbb {F}} n]$
we have
2.3 Generalized triangles
The (r-uniform) generalized triangle ![]() is the r-graph with vertex set
is the r-graph with vertex set
![]() $[2r-1]$
and edge set
$[2r-1]$
and edge set
Note that ![]() is simply a triangle.
is simply a triangle.
Fix
![]() $n \ge r \ge 2$
and
$n \ge r \ge 2$
and
![]() $\ell \ge r$
. Let
$\ell \ge r$
. Let
![]() $[n] = V_1 \cup \cdots \cup V_{\ell }$
be a partition such that
$[n] = V_1 \cup \cdots \cup V_{\ell }$
be a partition such that
![]() $|V_i| \in \left \{\lfloor \frac {n}{\ell }\rfloor , \lceil \frac {n}{\ell } \rceil \right \}$
for all
$|V_i| \in \left \{\lfloor \frac {n}{\ell }\rfloor , \lceil \frac {n}{\ell } \rceil \right \}$
for all
![]() $i\in [\ell ]$
. The generalized Turán r-graph
$i\in [\ell ]$
. The generalized Turán r-graph
![]() $T_{r}(n,\ell )$
is the r-graph on
$T_{r}(n,\ell )$
is the r-graph on
![]() $[n]$
whose edge set consists of all r-sets that contain at most one vertex from each
$[n]$
whose edge set consists of all r-sets that contain at most one vertex from each
![]() $V_i$
. Note that
$V_i$
. Note that
![]() $T_2(n,\ell )$
is the Turán graph
$T_2(n,\ell )$
is the Turán graph
![]() $T(n, \ell )$
. Let
$T(n, \ell )$
. Let
![]() $t_{r}(n,\ell )$
denote the number of edges in
$t_{r}(n,\ell )$
denote the number of edges in
![]() $T_{r}(n,\ell )$
.
$T_{r}(n,\ell )$
.

Figure 2: The generealized triangle ![]() and the Turán
and the Turán
![]() $3$
-graph
$3$
-graph
![]() $T_{3}(n,3)$
.
$T_{3}(n,3)$
.
Katona conjectured and Bollobás [Reference Bollobás8] proved that ![]() for all
for all
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
![]() $K_{4}^{3-}$
is the unique
$K_{4}^{3-}$
is the unique
![]() $3$
-graph with
$3$
-graph with
![]() $4$
vertices and
$4$
vertices and
![]() $3$
edges (see Figure 2). Later, Frankl and Füredi [Reference Frankl and Füredi24] sharpened the result of Bollobás by showing that
$3$
edges (see Figure 2). Later, Frankl and Füredi [Reference Frankl and Füredi24] sharpened the result of Bollobás by showing that ![]() for all
for all
![]() $n\ge 3000$
. In [Reference Keevash and Mubayi44], Keevash and Mubayi proved the edge-stability of
$n\ge 3000$
. In [Reference Keevash and Mubayi44], Keevash and Mubayi proved the edge-stability of ![]() and improved the lower bound of n from
and improved the lower bound of n from
![]() $3000$
to
$3000$
to
![]() $33$
. A short proof for the edge-stability with a linear dependency between the error parameters can be found in [Reference Liu49].
$33$
. A short proof for the edge-stability with a linear dependency between the error parameters can be found in [Reference Liu49].
The vertex-extendability of ![]() can be easily obtained from the proof of Lemma 4.4 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Therefore, we obtain the following result.
can be easily obtained from the proof of Lemma 4.4 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Therefore, we obtain the following result.
Theorem 2.3 There exist constants
![]() $N_0$
and
$N_0$
and ![]() such that for all integers
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and ![]() we have
we have
For
![]() $r = 4$
, improving a result of Sidorenko in [Reference Sidorenko74], Pikhurko proved in [Reference Pikhurko67] that
$r = 4$
, improving a result of Sidorenko in [Reference Sidorenko74], Pikhurko proved in [Reference Pikhurko67] that ![]() for all sufficiently large n.
for all sufficiently large n.
Similarly, the vertex-extendability of ![]() can be obtained from the proof of Lemma 4.4 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Therefore, we obtain the following result.
can be obtained from the proof of Lemma 4.4 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Therefore, we obtain the following result.
Theorem 2.4 There exist constants
![]() $N_0$
and
$N_0$
and ![]() such that for all integers
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and ![]() we have
we have
The situation becomes complicated when
![]() $r\ge 5$
. Let
$r\ge 5$
. Let ![]() denote the unique
denote the unique
![]() $5$
-graph with
$5$
-graph with
![]() $11$
vertices such that every
$11$
vertices such that every
![]() $4$
-set of vertices is contained in exactly one edge. Let
$4$
-set of vertices is contained in exactly one edge. Let ![]() denote the unique
denote the unique
![]() $6$
-graph with
$6$
-graph with
![]() $12$
vertices such that every
$12$
vertices such that every
![]() $5$
-set of vertices is contained in exactly one edge. Let
$5$
-set of vertices is contained in exactly one edge. Let ![]() and
and ![]() denote the maximum
denote the maximum ![]() -construction and
-construction and ![]() -construction on n vertices, respectively. Some calculations show that
-construction on n vertices, respectively. Some calculations show that ![]() and
and ![]() .
.
In [Reference Frankl and Füredi25], Frankl and Füredi proved that ![]() for
for
![]() $r =5,6$
. Much later, using a sophisticated stability argument, Norin and Yepremyan [Reference Norin and Yepremyan65] proved that
$r =5,6$
. Much later, using a sophisticated stability argument, Norin and Yepremyan [Reference Norin and Yepremyan65] proved that ![]() and
and ![]() are edge-stable with respect to
are edge-stable with respect to ![]() and
and ![]() respectively, and moreover,
respectively, and moreover, ![]() for
for
![]() $r =5,6$
and large n.
$r =5,6$
and large n.
It was observed by Pikhurko [Reference Pikhurko67] that both ![]() and
and ![]() fail to be degree-stable (or vertex-extendable). However, from [Reference Norin and Yepremyan65, 7.2, 7.4, and, Lemmas] one can easily observe that
fail to be degree-stable (or vertex-extendable). However, from [Reference Norin and Yepremyan65, 7.2, 7.4, and, Lemmas] one can easily observe that ![]() and
and ![]() are weakly vertex-extendable. Therefore, we obtain the following theorem.
are weakly vertex-extendable. Therefore, we obtain the following theorem.
Theorem 2.5 For
![]() $r\in \{5,6\}$
there exist constants
$r\in \{5,6\}$
there exist constants
![]() $N_0$
and
$N_0$
and ![]() such that for all integers
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and ![]() we have
we have
It seems that there are even no conjectures for the extremal constructions of ![]() when
when
![]() $r\ge 7$
. We refer the reader to [Reference Frankl and Füredi25] for some lower and upper bounds for
$r\ge 7$
. We refer the reader to [Reference Frankl and Füredi25] for some lower and upper bounds for ![]() in general.
in general.
2.4 The expansion of complete graphs
Fix integers
![]() $\ell \ge r \ge 2$
. The expansion
$\ell \ge r \ge 2$
. The expansion
![]() $H_{\ell +1}^{r}$
of the complete graph
$H_{\ell +1}^{r}$
of the complete graph
![]() $K_{\ell +1}$
is the r-graph obtained from
$K_{\ell +1}$
is the r-graph obtained from
![]() $K_{\ell +1}$
by adding a set of
$K_{\ell +1}$
by adding a set of
![]() $r-2$
new vertices into each edge of
$r-2$
new vertices into each edge of
![]() $K_{\ell +1}$
, and moreover, these new
$K_{\ell +1}$
, and moreover, these new
![]() $(r-2)$
-sets are pairwise disjoint (see Figure 3). It is clear from the definition that
$(r-2)$
-sets are pairwise disjoint (see Figure 3). It is clear from the definition that
![]() $H_{\ell +1}^{r}$
has
$H_{\ell +1}^{r}$
has
![]() $\ell +1+(r-2)\binom {\ell +1}{2}$
vertices and
$\ell +1+(r-2)\binom {\ell +1}{2}$
vertices and
![]() $\binom {\ell +1}{2}$
edges.
$\binom {\ell +1}{2}$
edges.
The r-graph
![]() $H_{\ell +1}^{r}$
was introduced by Mubayi [Reference Mubayi60] as a way to generalize Turán’s theorem to hypergraphs. These hypergraphs provide the first explicitly defined examples which yield an infinite family of numbers realizable as Turán densities for hypergraphs. In [Reference Mubayi60], Mubayi determined the Turán density of
$H_{\ell +1}^{r}$
was introduced by Mubayi [Reference Mubayi60] as a way to generalize Turán’s theorem to hypergraphs. These hypergraphs provide the first explicitly defined examples which yield an infinite family of numbers realizable as Turán densities for hypergraphs. In [Reference Mubayi60], Mubayi determined the Turán density of
![]() $H_{\ell +1}^{r}$
for all integers
$H_{\ell +1}^{r}$
for all integers
![]() $\ell \ge r \ge 3$
, and proved that
$\ell \ge r \ge 3$
, and proved that
![]() $H_{\ell +1}^{r}$
is edge-stable. In [Reference Pikhurko68], Pikhurko refined Mubayi’s result and proved that
$H_{\ell +1}^{r}$
is edge-stable. In [Reference Pikhurko68], Pikhurko refined Mubayi’s result and proved that
![]() $\mathrm {EX}(n, H_{\ell +1}^{r}) = \{T_r(n,\ell )\}$
for all integers
$\mathrm {EX}(n, H_{\ell +1}^{r}) = \{T_r(n,\ell )\}$
for all integers
![]() $\ell \ge r \ge 3$
when n is sufficiently large.
$\ell \ge r \ge 3$
when n is sufficiently large.
The vertex-extendability of
![]() $H_{\ell +1}^{r}$
can be easily obtained by a small modification of the proof of Lemma 4.8 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Therefore, we obtain the following result.
$H_{\ell +1}^{r}$
can be easily obtained by a small modification of the proof of Lemma 4.8 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Therefore, we obtain the following result.
Theorem 2.6 Fix integers
![]() $\ell \ge r \ge 2$
. There exist constants
$\ell \ge r \ge 2$
. There exist constants
![]() $N_0$
and
$N_0$
and
![]() $c = c(\ell , r)>0$
such that for all integers
$c = c(\ell , r)>0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t\in [0, c n]$
we have
$t\in [0, c n]$
we have
Remarks The definition of expansion can be extended to all graphs as follows. Fix a graph F, let the r-graph
![]() $H_{F}^{r}$
be obtained from F by adding a set of
$H_{F}^{r}$
be obtained from F by adding a set of
![]() $r-2$
new vertices into each edge of F, and moreover, these new
$r-2$
new vertices into each edge of F, and moreover, these new
![]() $(r-2)$
-sets are pairwise disjoint. Similar to Theorem 2.1, one could obtain a corresponding result for the expansion of all edge-critical graphs. We omit its statement and proof here.
$(r-2)$
-sets are pairwise disjoint. Similar to Theorem 2.1, one could obtain a corresponding result for the expansion of all edge-critical graphs. We omit its statement and proof here.
2.5 The expansion of hypergraphs
Given an r-graph F with
![]() $\ell +1$
vertices, the expansion
$\ell +1$
vertices, the expansion
![]() $H^{F}_{\ell +1}$
of F is the r-graph obtained from F by adding, for every pair
$H^{F}_{\ell +1}$
of F is the r-graph obtained from F by adding, for every pair
![]() $\{u,v\}\subset V(F)$
that is not contained in any edge of F, an
$\{u,v\}\subset V(F)$
that is not contained in any edge of F, an
![]() $(r-2)$
-set of new vertices, and moreover, these
$(r-2)$
-set of new vertices, and moreover, these
![]() $(r-2)$
-sets are pairwise disjoint. It is easy to see that the expansion of the empty r-graph on
$(r-2)$
-sets are pairwise disjoint. It is easy to see that the expansion of the empty r-graph on
![]() $\ell +1$
vertices (here empty means that the edge set is empty) is the same as the expansion of the complete graph
$\ell +1$
vertices (here empty means that the edge set is empty) is the same as the expansion of the complete graph
![]() $K_{\ell +1}$
defined in the previous subsection. However, in general, these two definitions are different.
$K_{\ell +1}$
defined in the previous subsection. However, in general, these two definitions are different.

Figure 3: The expansion
![]() $H_{4}^3$
of
$H_{4}^3$
of
![]() $K_4$
and the Turán
$K_4$
and the Turán
![]() $3$
-graph
$3$
-graph
![]() $T_{3}(n,3)$
.
$T_{3}(n,3)$
.
Our first result in this subsection is about the expansion of the expanded trees. Given a tree T on k vertices, define the
![]() $(r-2)$
-expansion
$(r-2)$
-expansion
![]() $\mathrm {Exp}(T)$
of T as
$\mathrm {Exp}(T)$
of T as
where A is a set of
![]() $r-2$
new vertices that is disjoint from
$r-2$
new vertices that is disjoint from
![]() $V(T)$
.
$V(T)$
.
Given a tree T on k vertices, we say T is an Erdős–Sós tree if it satisfies the famous Erdős–Sós conjecture on trees. In other words, T is contained in every graph with average degree more than
![]() $k-2$
. In [Reference Sidorenko75], Sidorenko proved that for large k, if T is an Erdős–Sós tree on k vertices, then
$k-2$
. In [Reference Sidorenko75], Sidorenko proved that for large k, if T is an Erdős–Sós tree on k vertices, then
![]() $\mathrm {ex}(n,H^{\mathrm {Exp}(T)}_{k+r-2}) \le t_{r}(n, k+r-3) + o(n^{r})$
. Much later, Norin and Yepremyan [Reference Norin and Yepremyan66], and independently, Brandt, Irwin, and Jiang [Reference Brandt, Irwin and Jiang9], improved Sidorenko’s result by showing that, under the same setting,
$\mathrm {ex}(n,H^{\mathrm {Exp}(T)}_{k+r-2}) \le t_{r}(n, k+r-3) + o(n^{r})$
. Much later, Norin and Yepremyan [Reference Norin and Yepremyan66], and independently, Brandt, Irwin, and Jiang [Reference Brandt, Irwin and Jiang9], improved Sidorenko’s result by showing that, under the same setting,
![]() $H^{\mathrm {Exp}(T)}_{k+r-2}$
is edge-stable with respect to
$H^{\mathrm {Exp}(T)}_{k+r-2}$
is edge-stable with respect to
![]() $K_{k+r-3}^{r}$
and
$K_{k+r-3}^{r}$
and
![]() $\mathrm {EX}(n,H^{\mathrm {Exp}(T)}_{k+r-2}) = \{T_r(n,k+r-3)\}$
for large n. In fact, it follows easily from [Reference Norin and Yepremyan66, 3.5, 4.1, and, Lemmas] that
$\mathrm {EX}(n,H^{\mathrm {Exp}(T)}_{k+r-2}) = \{T_r(n,k+r-3)\}$
for large n. In fact, it follows easily from [Reference Norin and Yepremyan66, 3.5, 4.1, and, Lemmas] that
![]() $H^{\mathrm {Exp}(T)}_{k+r-2}$
is weakly vertex-extendable with respect to
$H^{\mathrm {Exp}(T)}_{k+r-2}$
is weakly vertex-extendable with respect to
![]() $K_{k+r-3}^{r}$
. Hence, we obtain the following result.
$K_{k+r-3}^{r}$
. Hence, we obtain the following result.
Theorem 2.7 For every integer
![]() $r\ge 3$
there exists
$r\ge 3$
there exists
![]() $M_{r}$
such that if T is an Erdős–Sós tree on
$M_{r}$
such that if T is an Erdős–Sós tree on
![]() $k\ge M_r$
vertices, then there exist
$k\ge M_r$
vertices, then there exist
![]() $N_0$
and
$N_0$
and
![]() $c_T>0$
such that for all integers
$c_T>0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t \le c_T n$
, we have
$t \le c_T n$
, we have
Next, we consider the expansion of a different class of hypergraphs. Let
![]() $B(r, \ell +1)$
be the r-graph with vertex set
$B(r, \ell +1)$
be the r-graph with vertex set
![]() $[\ell +1]$
and edge set
$[\ell +1]$
and edge set
Recall that the Lagrangian of an r-graph
![]() $\mathcal {H}$
(by viewing
$\mathcal {H}$
(by viewing
![]() $\mathcal {H}$
as a pattern) is denoted by
$\mathcal {H}$
as a pattern) is denoted by
![]() $\lambda (\mathcal {H})$
. For integers
$\lambda (\mathcal {H})$
. For integers
![]() $\ell \ge r \ge 2$
let the family
$\ell \ge r \ge 2$
let the family
![]() $\mathcal {F}_{\ell +1}^r$
be the collection of r-graphs F with the following properties:
$\mathcal {F}_{\ell +1}^r$
be the collection of r-graphs F with the following properties:
-
(a)
 $\sup \left \{\lambda (\mathcal {H}) \colon \mathcal {H} \text {is} F\text {-free and not a} K_{\ell }^r\text {-subconstruction}\right \} < \frac {\ell \cdots (\ell -r+1)}{\ell ^r}$
, and
$\sup \left \{\lambda (\mathcal {H}) \colon \mathcal {H} \text {is} F\text {-free and not a} K_{\ell }^r\text {-subconstruction}\right \} < \frac {\ell \cdots (\ell -r+1)}{\ell ^r}$
, and -
(b) either F has an isolated vertex or
 $F\subset B(r, \ell +1)$
.
$F\subset B(r, \ell +1)$
.
For every
![]() $F\in \mathcal {F}_{\ell +1}^r$
the vertex-extendabilityFootnote
3
of the expansion
$F\in \mathcal {F}_{\ell +1}^r$
the vertex-extendabilityFootnote
3
of the expansion
![]() $H_{\ell +1}^{F}$
can be easily obtained by a small modification of the proof of Lemma 4.8 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Hence, we obtain the following result.
$H_{\ell +1}^{F}$
can be easily obtained by a small modification of the proof of Lemma 4.8 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Hence, we obtain the following result.
Theorem 2.8 Suppose that
![]() $\ell \ge r\ge 2$
are integers and
$\ell \ge r\ge 2$
are integers and
![]() $F\in \mathcal {F}_{\ell +1}^r$
. Then there exist constants
$F\in \mathcal {F}_{\ell +1}^r$
. Then there exist constants
![]() $N_0$
and
$N_0$
and
![]() $c_F> 0$
such that for all integers
$c_F> 0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t\in [0, c_F n]$
, we have
$t\in [0, c_F n]$
, we have
Remarks
-
• In [Reference Mubayi and Pikhurko63], Mubayi and Pikhurko considered the Turán problem for the r-graph
 $\mathrm {Fan}^r$
(the generalized Fan), which is the expansion of the r-graph on
$\mathrm {Fan}^r$
(the generalized Fan), which is the expansion of the r-graph on
 $r+1$
vertices with only one edge. It is easy to see that
$r+1$
vertices with only one edge. It is easy to see that
 $\mathrm {Fan}^r$
is a member in
$\mathrm {Fan}^r$
is a member in
 $\mathcal {F}_{r+1}^{r}$
.
$\mathcal {F}_{r+1}^{r}$
. -
• The Turán problem for the expansion of certain class of r-graphs (which is a proper subfamily of
 $\mathcal {F}_{\ell +1}^r$
) were studied previously in [Reference Brandt, Irwin and Jiang9] and [Reference Norin and Yepremyan66].
$\mathcal {F}_{\ell +1}^r$
) were studied previously in [Reference Brandt, Irwin and Jiang9] and [Reference Norin and Yepremyan66]. -
• Let
 $M_{k}^{r}$
denote the r-graph consisting of k vertex-disjoint edges (i.e., a matching of size k) and let
$M_{k}^{r}$
denote the r-graph consisting of k vertex-disjoint edges (i.e., a matching of size k) and let
 $L_{k}^{r}$
denote the r-graph consisting of k edges having one vertex, say v, in common, and every pair of edges interest only at v (i.e., a k-edge sunflower with the center v). By results in [Reference Hefetz and Keevash33, Reference Jiang, Peng and Wu40], if F is isomorphic to
$L_{k}^{r}$
denote the r-graph consisting of k edges having one vertex, say v, in common, and every pair of edges interest only at v (i.e., a k-edge sunflower with the center v). By results in [Reference Hefetz and Keevash33, Reference Jiang, Peng and Wu40], if F is isomorphic to
 $M_{k}^{3}$
(see [Reference Hefetz and Keevash33] for
$M_{k}^{3}$
(see [Reference Hefetz and Keevash33] for
 $k=2$
and [Reference Jiang, Peng and Wu40] for
$k=2$
and [Reference Jiang, Peng and Wu40] for
 $k \ge 3$
),
$k \ge 3$
),
 $L_{k}^{3}$
(see [Reference Jiang, Peng and Wu40]), or
$L_{k}^{3}$
(see [Reference Jiang, Peng and Wu40]), or
 $L_{k}^4$
(see [Reference Jiang, Peng and Wu40]), where
$L_{k}^4$
(see [Reference Jiang, Peng and Wu40]), where
 $k \ge 2$
is an integer, then F is contained in
$k \ge 2$
is an integer, then F is contained in
 $\mathcal {F}_{\ell +1}^r$
.
$\mathcal {F}_{\ell +1}^r$
.
Now we focus on the expansion of r-uniform matching of size two with
![]() $r\ge 4$
. We say an r-graph is semibipartite if its vertex set can be partitioned into two parts
$r\ge 4$
. We say an r-graph is semibipartite if its vertex set can be partitioned into two parts
![]() $V_1$
and
$V_1$
and
![]() $V_2$
such that every edge contains exactly one vertex in
$V_2$
such that every edge contains exactly one vertex in
![]() $V_1$
. Let
$V_1$
. Let
![]() $S_r(n)$
denote the semibipartite r-graph on n vertices with the maximum number of edges. Simple calculations show that
$S_r(n)$
denote the semibipartite r-graph on n vertices with the maximum number of edges. Simple calculations show that
![]() $|S_r(n)| \sim \left (\frac {r-1}{r}\right )^{r-1}\binom {n}{r}$
.
$|S_r(n)| \sim \left (\frac {r-1}{r}\right )^{r-1}\binom {n}{r}$
.
Confirming a conjecture of Hefetz and Keevash [Reference Hefetz and Keevash33], Bene Watts, Norin, and Yepremyan [Reference Bene Watts, Norin and Yepremyan7] showed that for
![]() $r\ge 4$
,
$r\ge 4$
,
![]() $\mathrm {EX}\left (n, H_{2r}^{M_{2}^{r}}\right ) = \{S_r(n)\}$
for all sufficiently large n.
$\mathrm {EX}\left (n, H_{2r}^{M_{2}^{r}}\right ) = \{S_r(n)\}$
for all sufficiently large n.
The vertex-extendabilityFootnote
4
of
![]() $H_{2r}^{M_{2}^{r}}$
can be easily obtained by a small modification of the proof of Lemma 4.12 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Hence we have the following result.
$H_{2r}^{M_{2}^{r}}$
can be easily obtained by a small modification of the proof of Lemma 4.12 in [Reference Liu, Mubayi and Reiher51] (also see the Concluding Remarks in [Reference Liu, Mubayi and Reiher51]). Hence we have the following result.
Theorem 2.9 For every integer
![]() $r \ge 4$
, there exist constants
$r \ge 4$
, there exist constants
![]() $N_0$
and
$N_0$
and
![]() $c = c(r)> 0$
such that for all integers
$c = c(r)> 0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t\in [0, c n]$
, we have
$t\in [0, c n]$
, we have
Remark It is quite possible that Theorem 1.5 applies to the expansion of other hypergraphs, for example, the
![]() $3$
-graph defined in [Reference Yan and Peng79] which provides the first example of a single hypergraph whose Turán density is an irrational number.
$3$
-graph defined in [Reference Yan and Peng79] which provides the first example of a single hypergraph whose Turán density is an irrational number.
2.6 Expanded triangles
Let
![]() $\mathcal {C}^{2r}_{3}$
denote the
$\mathcal {C}^{2r}_{3}$
denote the
![]() $2r$
-graph with vertex set
$2r$
-graph with vertex set
![]() $[3r]$
and edge set
$[3r]$
and edge set
Let
![]() $[n]= V_1 \cup V_2$
be a partition such that
$[n]= V_1 \cup V_2$
be a partition such that
![]() $|V_1| = \lfloor n/2 \rfloor +m$
. Let
$|V_1| = \lfloor n/2 \rfloor +m$
. Let
![]() $B_{2r}^{\mathrm {odd}}(n,m)$
denote the
$B_{2r}^{\mathrm {odd}}(n,m)$
denote the
![]() $2r$
-graph on
$2r$
-graph on
![]() $[n]$
whose edge set consists of all
$[n]$
whose edge set consists of all
![]() $2r$
-sets that interest
$2r$
-sets that interest
![]() $V_1$
in odd number of vertices (see Figure 4). Some calculations show that
$V_1$
in odd number of vertices (see Figure 4). Some calculations show that
![]() $\max _{m}|B_{2r}^{\mathrm {odd}}(n,m)|\sim \frac {1}{2}\binom {n}{2r}$
. Let
$\max _{m}|B_{2r}^{\mathrm {odd}}(n,m)|\sim \frac {1}{2}\binom {n}{2r}$
. Let
![]() $B_{2r}^{\mathrm {odd}} = (2,E)$
denote the pattern such that E consists of all
$B_{2r}^{\mathrm {odd}} = (2,E)$
denote the pattern such that E consists of all
![]() $2r$
-multisets that contain exactly odd number of
$2r$
-multisets that contain exactly odd number of
![]() $1$
s. Note that
$1$
s. Note that
![]() $B_{2r}^{\mathrm {odd}}(n,m)$
is a
$B_{2r}^{\mathrm {odd}}(n,m)$
is a
![]() $B_{2r}^{\mathrm {odd}}$
-construction.
$B_{2r}^{\mathrm {odd}}$
-construction.

Figure 4: The
![]() $4$
-graph
$4$
-graph
![]() $\mathcal {C}_{3}^{4}$
(expanded triangle) and the
$\mathcal {C}_{3}^{4}$
(expanded triangle) and the
![]() $4$
-graph
$4$
-graph
![]() $B_{4}^{\mathrm {odd}}(n)$
.
$B_{4}^{\mathrm {odd}}(n)$
.
The Turán problem for
![]() $\mathcal {C}^{2r}_{3}$
was first considered by Frankl [Reference Frankl20], who proved that
$\mathcal {C}^{2r}_{3}$
was first considered by Frankl [Reference Frankl20], who proved that
![]() $\pi (\mathcal {C}^{2r}_{3}) = 1/2$
. Later, Keevash and Sudakov [Reference Keevash and Sudakov45] proved that
$\pi (\mathcal {C}^{2r}_{3}) = 1/2$
. Later, Keevash and Sudakov [Reference Keevash and Sudakov45] proved that
![]() $\mathcal {C}^{2r}_{3}$
is edge-stable with respect to
$\mathcal {C}^{2r}_{3}$
is edge-stable with respect to
![]() $B_{2r}^{\mathrm {odd}}$
, and moreover,
$B_{2r}^{\mathrm {odd}}$
, and moreover,
![]() $\mathrm {EX}(n,\mathcal {C}^{2r}_{3}) \subset \left \{B_{2r}^{\mathrm {odd}}(n,m)\colon m\in [0,n/2]\right \}$
. Simple constructionsFootnote
5
show that
$\mathrm {EX}(n,\mathcal {C}^{2r}_{3}) \subset \left \{B_{2r}^{\mathrm {odd}}(n,m)\colon m\in [0,n/2]\right \}$
. Simple constructionsFootnote
5
show that
![]() $\mathcal {C}^{2r}_{3}$
is not degree-stable (or vertex-extendable) with respect to
$\mathcal {C}^{2r}_{3}$
is not degree-stable (or vertex-extendable) with respect to
![]() $B_{2r}^{\mathrm {odd}}$
. However, using [Reference Keevash and Sudakov45, 3.5, Claim], one can easily show that
$B_{2r}^{\mathrm {odd}}$
. However, using [Reference Keevash and Sudakov45, 3.5, Claim], one can easily show that
![]() $\mathcal {C}^{2r}_{3}$
is weakly vertex-extendable with respect to
$\mathcal {C}^{2r}_{3}$
is weakly vertex-extendable with respect to
![]() $B_{2r}^{\mathrm {odd}}$
. Hence, we have the following theorem.
$B_{2r}^{\mathrm {odd}}$
. Hence, we have the following theorem.
Theorem 2.10 For every integer
![]() $r \ge 2$
there exist constants
$r \ge 2$
there exist constants
![]() $N_0$
and
$N_0$
and
![]() $c> 0$
such that for all integers
$c> 0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t\in [0, c n]$
, we have
$t\in [0, c n]$
, we have
Remarks
-
• Calculations in [Reference Keevash and Sudakov45] show that if
 $B_{2r}^{\mathrm {odd}}(n,m)$
is an optimal
$B_{2r}^{\mathrm {odd}}(n,m)$
is an optimal
 $B_{2r}^{\mathrm {odd}}$
-construction, then
$B_{2r}^{\mathrm {odd}}$
-construction, then
 $m < \sqrt {2rn}$
. So it suffices to consider m in the range
$m < \sqrt {2rn}$
. So it suffices to consider m in the range
 $\left [0,\sqrt {2r(n-t)}\right ]$
for Theorem 2.10.
$\left [0,\sqrt {2r(n-t)}\right ]$
for Theorem 2.10. -
• In general, one could consider the expanded
 $K_{\ell +1}$
for
$K_{\ell +1}$
for
 $\ell \ge 3$
. It seems that the above theorem can be extended to these hypergraphs in some cases. We refer the reader to [Reference Sidorenko73] and [Reference Keevash and Sudakov45] for more details.
$\ell \ge 3$
. It seems that the above theorem can be extended to these hypergraphs in some cases. We refer the reader to [Reference Sidorenko73] and [Reference Keevash and Sudakov45] for more details.
2.7 Hypergraph books
Let
![]() $F_7$
(
$F_7$
(
![]() $4$
-book with
$4$
-book with
![]() $3$
-pages) denote the
$3$
-pages) denote the
![]() $3$
-graph with vertex set
$3$
-graph with vertex set
![]() $\{1,2,3,4,5,6,7\}$
and edge set
$\{1,2,3,4,5,6,7\}$
and edge set
Let
![]() $B_{4}^{\mathrm {even}}(n)$
denote the maximum
$B_{4}^{\mathrm {even}}(n)$
denote the maximum
![]() $B_{4}^{\mathrm {even}}:=\left (2, \{1,1,2,2\}\right )$
-construction on n vertices (see Figure 5). Simply calculations show that
$B_{4}^{\mathrm {even}}:=\left (2, \{1,1,2,2\}\right )$
-construction on n vertices (see Figure 5). Simply calculations show that
![]() $|B_4(n)| \sim \frac {3}{8}\binom {n}{4}$
.
$|B_4(n)| \sim \frac {3}{8}\binom {n}{4}$
.

Figure 5: The
![]() $4$
-graph
$4$
-graph
![]() $F_7$
(
$F_7$
(
![]() $4$
-book with
$4$
-book with
![]() $3$
pages) and the
$3$
pages) and the
![]() $4$
-graph
$4$
-graph
![]() $B_{4}^{\mathrm {even}}(n)$
.
$B_{4}^{\mathrm {even}}(n)$
.
Füredi, Pikhurko, and Simonovits [Reference Füredi, Pikhurko and Simonovits29] proved that
![]() $\mathrm {EX}(n, F_7) = \{B_4(n)\}$
for all sufficiently large n. Moreover, they proved that
$\mathrm {EX}(n, F_7) = \{B_4(n)\}$
for all sufficiently large n. Moreover, they proved that
![]() $F_7$
is degree-stable. Hence, we obtain the following result.
$F_7$
is degree-stable. Hence, we obtain the following result.
Theorem 2.11 There exist constants
![]() $N_0$
and
$N_0$
and
![]() $c> 0$
such that for all integers
$c> 0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t\in [0, c n]$
, we have
$t\in [0, c n]$
, we have
Let
![]() $\mathbb {F}_{4,3}$
denote the
$\mathbb {F}_{4,3}$
denote the
![]() $4$
-graph with vertex set
$4$
-graph with vertex set
![]() $\{1,2,3,4,5,6,7\}$
and edge set
$\{1,2,3,4,5,6,7\}$
and edge set
Let
![]() $B_{4}^{\mathrm {odd}}(n,m)$
denote the
$B_{4}^{\mathrm {odd}}(n,m)$
denote the
![]() $B_4^{\mathrm {odd}}:=\left (2, \{\{1,2,2,2\}, \{1,1,1,2\}\}\right )$
-construction (see Figure 6) on n vertices with one part of size
$B_4^{\mathrm {odd}}:=\left (2, \{\{1,2,2,2\}, \{1,1,1,2\}\}\right )$
-construction (see Figure 6) on n vertices with one part of size
![]() $\lfloor n/2 \rfloor + m$
. Recall from the previous subsection that
$\lfloor n/2 \rfloor + m$
. Recall from the previous subsection that
![]() $\max _{m}|B_{4}^{\mathrm {odd}}(n,m)| \sim \frac {1}{2}\binom {n}{4}$
.
$\max _{m}|B_{4}^{\mathrm {odd}}(n,m)| \sim \frac {1}{2}\binom {n}{4}$
.

Figure 6: The
![]() $4$
-graph
$4$
-graph
![]() $\mathbb {F}_{4,3}$
and the
$\mathbb {F}_{4,3}$
and the
![]() $4$
-graph
$4$
-graph
![]() $B_{4}^{\mathrm {odd}}(n)$
.
$B_{4}^{\mathrm {odd}}(n)$
.
Füredi, Mubayi, and Pikhurko [Reference Füredi, Mubayi and Pikhurko27] proved that
![]() $\mathrm {EX}(n, \mathbb {F}_{4,3}) \subset \{B_{4}^{\mathrm {odd}}(n,m) \colon m \in [0,n/2]\}$
for large n, and moreover,
$\mathrm {EX}(n, \mathbb {F}_{4,3}) \subset \{B_{4}^{\mathrm {odd}}(n,m) \colon m \in [0,n/2]\}$
for large n, and moreover,
![]() $\mathbb {F}_{4,3}$
is edge-stable with respect to
$\mathbb {F}_{4,3}$
is edge-stable with respect to
![]() $B_4^{\mathrm {odd}}$
. They also showed that edge-stable cannot be replaced by degree-stable (or vertex-extendable). However, from [Reference Füredi, Mubayi and Pikhurko27, 3.1, Lemma] one can easily obtain that
$B_4^{\mathrm {odd}}$
. They also showed that edge-stable cannot be replaced by degree-stable (or vertex-extendable). However, from [Reference Füredi, Mubayi and Pikhurko27, 3.1, Lemma] one can easily obtain that
![]() $\mathbb {F}_{4,3}$
is weakly edge-stable with respect to
$\mathbb {F}_{4,3}$
is weakly edge-stable with respect to
![]() $B_4^{\mathrm {odd}}$
. Hence, we obtain the following theorem.
$B_4^{\mathrm {odd}}$
. Hence, we obtain the following theorem.
Theorem 2.12 There exist constants
![]() $N_0$
and
$N_0$
and
![]() $c> 0$
such that for all integers
$c> 0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t\in [0, c n]$
, we have
$t\in [0, c n]$
, we have
Let
![]() $\mathbb {F}_{3,2}$
denote the
$\mathbb {F}_{3,2}$
denote the
![]() $3$
-graph with vertex set
$3$
-graph with vertex set
![]() $\{1,2,3,4,5\}$
and edge set
$\{1,2,3,4,5\}$
and edge set
Recall that
![]() $S_{3}(n)$
is the semibipartite
$S_{3}(n)$
is the semibipartite
![]() $3$
-graph on n vertices with the maximum number of edges, i.e., the maximum
$3$
-graph on n vertices with the maximum number of edges, i.e., the maximum
![]() $S_3:=\left (2, \{1,2,2\}\right )$
-construction on n vertices (see Figure 7).
$S_3:=\left (2, \{1,2,2\}\right )$
-construction on n vertices (see Figure 7).

Figure 7: The
![]() $3$
-graph
$3$
-graph
![]() $\mathbb {F}_{3,2}$
and the semibipartite
$\mathbb {F}_{3,2}$
and the semibipartite
![]() $3$
-graph
$3$
-graph
![]() $S_3(n)$
.
$S_3(n)$
.
Füredi, Pikhurko, and Simonovits [Reference Füredi, Pikhurko and Simonovits28] proved that
![]() $\mathrm {EX}(n, \mathbb {F}_{3,2}) = \{S_3(n)\}$
for all sufficiently large n. A construction in their paper ([Reference Füredi, Pikhurko and Simonovits28, Construction 1.2]) shows that
$\mathrm {EX}(n, \mathbb {F}_{3,2}) = \{S_3(n)\}$
for all sufficiently large n. A construction in their paper ([Reference Füredi, Pikhurko and Simonovits28, Construction 1.2]) shows that
![]() $\mathbb {F}_{3,2}$
is not vertex-extendable with respect
$\mathbb {F}_{3,2}$
is not vertex-extendable with respect
![]() $S_3$
. But we will present a short proof in Section 5 which shows that
$S_3$
. But we will present a short proof in Section 5 which shows that
![]() $\mathbb {F}_{3,2}$
is weakly vertex-extendable with respect to
$\mathbb {F}_{3,2}$
is weakly vertex-extendable with respect to
![]() $S_3$
. Hence, we obtain the following result.
$S_3$
. Hence, we obtain the following result.
Theorem 2.13 There exist constants
![]() $N_0$
and
$N_0$
and
![]() $c> 0$
such that for all integers
$c> 0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t\in [0, c n]$
, we have
$t\in [0, c n]$
, we have
3 Proofs of Theorems 1.5 and 1.6
In this section, we prove Theorems 1.5 and 1.6. In fact, we will prove the following more general (but also more technical) version.
Theorem 3.1 Let
![]() $m \ge r \ge 2$
be integers and F be a nondegenerate r-graph on m vertices. Let
$m \ge r \ge 2$
be integers and F be a nondegenerate r-graph on m vertices. Let
![]() $f \colon \mathbb {N}\to \mathbb {R}$
be a nondecreasing function. Suppose that for all sufficiently large
$f \colon \mathbb {N}\to \mathbb {R}$
be a nondecreasing function. Suppose that for all sufficiently large
![]() $n\in \mathbb {N} \colon $
$n\in \mathbb {N} \colon $
-
(a)
 $\mathrm {ex}(n, F)$
is
$\mathrm {ex}(n, F)$
is
 $\frac {1-\pi (F)}{8m}\binom {n}{r-1}$
-smooth, and
$\frac {1-\pi (F)}{8m}\binom {n}{r-1}$
-smooth, and -
(b) F is
 $\left (f(n), \frac {1-\pi (F)}{4m} \binom {n}{r-1}\right )$
-bounded.
$\left (f(n), \frac {1-\pi (F)}{4m} \binom {n}{r-1}\right )$
-bounded.
Then there exists
![]() $N_0$
such that the following statements hold for all integers
$N_0$
such that the following statements hold for all integers
![]() $n, t \in \mathbb {N}$
with
$n, t \in \mathbb {N}$
with
-
(i) If a collection
 $\{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\}$
of n-vertex r-graphs on the same vertex set satisfies then
$\{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\}$
of n-vertex r-graphs on the same vertex set satisfies then $$ \begin{align*} |\mathcal{H}_i|> \binom{n}{r} - \binom{n-t}{r} + \mathrm{ex}(n-t, F) \quad\text{for all } i\in [t+1], \end{align*} $$
$$ \begin{align*} |\mathcal{H}_i|> \binom{n}{r} - \binom{n-t}{r} + \mathrm{ex}(n-t, F) \quad\text{for all } i\in [t+1], \end{align*} $$
 $\{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\}$
contains a rainbow F-matching.
$\{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\}$
contains a rainbow F-matching.
-
(ii) We have
 .
.
3.1 Preparations
First, recall the following result due to Katona, Nemetz, and Simonovits [Reference Katona, Nemetz and Simonovits41]
Proposition 3.2 (Katona–Nemetz–Simonovits [Reference Katona, Nemetz and Simonovits41])
Fix an r-graph F. The ratio
![]() $\frac {\mathrm {ex}(n,F)}{\binom {n}{r}}$
is nonincreasing in n. In particular,
$\frac {\mathrm {ex}(n,F)}{\binom {n}{r}}$
is nonincreasing in n. In particular,
![]() $\mathrm {ex}(n,F) \ge \pi (F)\binom {n}{r}$
for all
$\mathrm {ex}(n,F) \ge \pi (F)\binom {n}{r}$
for all
![]() $n\in \mathbb {N}$
, and
$n\in \mathbb {N}$
, and
 $$ \begin{align*} \pi(F) \le \frac{\mathrm{ex}(v(F),F)}{\binom{v(F)}{r}} \le \frac{\binom{v(F)}{r}-1}{\binom{v(F)}{r}}<1. \end{align*} $$
$$ \begin{align*} \pi(F) \le \frac{\mathrm{ex}(v(F),F)}{\binom{v(F)}{r}} \le \frac{\binom{v(F)}{r}-1}{\binom{v(F)}{r}}<1. \end{align*} $$
Next, we prove two simple inequalities concerning binomials.
Lemma 3.3 Suppose that
![]() $m \le n/r -1$
. Then
$m \le n/r -1$
. Then
 $$ \begin{align} \binom{n}{r}-\binom{n-m}{r} =\sum_{i=1}^{r}\binom{m}{i}\binom{n-m}{r-i} \le 2m\binom{n-m}{r-1}. \end{align} $$
$$ \begin{align} \binom{n}{r}-\binom{n-m}{r} =\sum_{i=1}^{r}\binom{m}{i}\binom{n-m}{r-i} \le 2m\binom{n-m}{r-1}. \end{align} $$
Proof For every
![]() $i\in [2,r]$
we have
$i\in [2,r]$
we have
 $$ \begin{align*} \frac{\binom{m}{i} \binom{n-m}{r-i}}{\binom{m}{i-1}\binom{n-m}{r-i+1}} = \frac{m-i+1}{i}\frac{r-i+1}{n-m-r+i} \le \frac{(r-1)m}{2(n-m-r)} \le \frac{1}{2}, \end{align*} $$
$$ \begin{align*} \frac{\binom{m}{i} \binom{n-m}{r-i}}{\binom{m}{i-1}\binom{n-m}{r-i+1}} = \frac{m-i+1}{i}\frac{r-i+1}{n-m-r+i} \le \frac{(r-1)m}{2(n-m-r)} \le \frac{1}{2}, \end{align*} $$
where the last inequality follows from the assumption that
![]() $m \le n/r -1$
. Therefore,
$m \le n/r -1$
. Therefore,
 $$ \begin{align*} \sum_{i=1}^{r}\binom{m}{i}\binom{n-m}{r-i} \le \sum_{i=1}^{r}\left(\frac{1}{2}\right)^{i-1} m \binom{n-m}{r-1} \le 2 m \binom{n-m}{r-1}, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{r}\binom{m}{i}\binom{n-m}{r-i} \le \sum_{i=1}^{r}\left(\frac{1}{2}\right)^{i-1} m \binom{n-m}{r-1} \le 2 m \binom{n-m}{r-1}, \end{align*} $$
proving Lemma 3.3.
Lemma 3.4 Suppose that integers
![]() $n,b,r \ge 1$
satisfy
$n,b,r \ge 1$
satisfy
![]() $b \le \frac {n-r}{r+1}$
. Then
$b \le \frac {n-r}{r+1}$
. Then
Proof For every
![]() $i \in [b]$
it follows from
$i \in [b]$
it follows from
![]() $b \le \frac {n-r}{r+1}$
that
$b \le \frac {n-r}{r+1}$
that
![]() $\frac {n-i}{n-i-r} = 1+ \frac {r}{n-i-r} \le 1+ \frac {r}{n-b-r} \le 1+ \frac {1}{b}$
. Therefore,
$\frac {n-i}{n-i-r} = 1+ \frac {r}{n-i-r} \le 1+ \frac {r}{n-b-r} \le 1+ \frac {1}{b}$
. Therefore,
 $$ \begin{align*} \binom{n}{r} = \prod_{i=0}^{b-1}\frac{n-i}{n-i-r} \binom{n-b}{r} \le \left(1+ \frac{1}{b}\right)^b \binom{n-b}{r} \le e \binom{n-b}{r}, \end{align*} $$
$$ \begin{align*} \binom{n}{r} = \prod_{i=0}^{b-1}\frac{n-i}{n-i-r} \binom{n-b}{r} \le \left(1+ \frac{1}{b}\right)^b \binom{n-b}{r} \le e \binom{n-b}{r}, \end{align*} $$
proving Lemma 3.4.
The following lemma says that
![]() $d(n,F)$
is well-behaved for every F.
$d(n,F)$
is well-behaved for every F.
Lemma 3.5 Let F be an r-graph. For every n and
![]() $m \le n/r -1$
we have
$m \le n/r -1$
we have
Proof It follows from Proposition 3.2 that
![]() $\mathrm {ex}(n,F)/\binom {n}{r} \le \mathrm {ex}(n-m,F)/\binom {n-m}{r}$
. Therefore,
$\mathrm {ex}(n,F)/\binom {n}{r} \le \mathrm {ex}(n-m,F)/\binom {n-m}{r}$
. Therefore,
 $$ \begin{align*} \mathrm{ex}(n,F) - \mathrm{ex}(n-m,F) & \le \frac{\binom{n}{r}}{\binom{n-m}{r}}\mathrm{ex}(n-m,F) - \mathrm{ex}(n-m,F) \\ & = \frac{\binom{n}{r}-\binom{n-m}{r}}{\binom{n-m}{r}}\mathrm{ex}(n-m,F) \\ &\hspace{-14pt} \overset{\text{Lemma~} 3.3}\le \frac{2m \binom{n-m}{r-1}}{\binom{n-m}{r}}\mathrm{ex}(n-m,F) = \frac{2mr}{n-m-r+1}\mathrm{ex}(n-m,F). \end{align*} $$
$$ \begin{align*} \mathrm{ex}(n,F) - \mathrm{ex}(n-m,F) & \le \frac{\binom{n}{r}}{\binom{n-m}{r}}\mathrm{ex}(n-m,F) - \mathrm{ex}(n-m,F) \\ & = \frac{\binom{n}{r}-\binom{n-m}{r}}{\binom{n-m}{r}}\mathrm{ex}(n-m,F) \\ &\hspace{-14pt} \overset{\text{Lemma~} 3.3}\le \frac{2m \binom{n-m}{r-1}}{\binom{n-m}{r}}\mathrm{ex}(n-m,F) = \frac{2mr}{n-m-r+1}\mathrm{ex}(n-m,F). \end{align*} $$
Consequently,
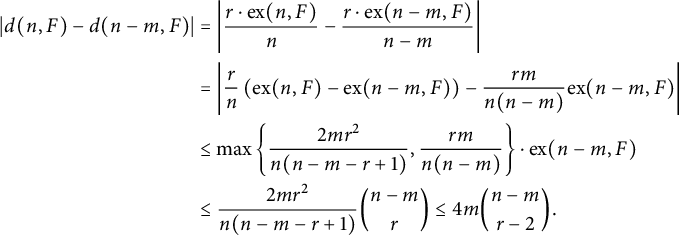 $$ \begin{align*} \left| d(n,F) - d(n-m, F) \right| & =\left| \frac{r\cdot \mathrm{ex}(n,F)}{n} - \frac{r\cdot \mathrm{ex}(n-m,F)}{n-m} \right| \\ & = \left| \frac{r}{n}\left(\mathrm{ex}(n,F)-\mathrm{ex}(n-m,F)\right) - \frac{rm}{n(n-m)}\mathrm{ex}(n-m,F) \right|\\ & \le \max\left\{ \frac{2mr^2}{n(n-m-r+1)},\frac{rm}{n(n-m)} \right\} \cdot \mathrm{ex}(n-m,F) \\ & \le \frac{2mr^2}{n(n-m-r+1)} \binom{n-m}{r} \le 4m \binom{n-m}{r-2}. \end{align*} $$
$$ \begin{align*} \left| d(n,F) - d(n-m, F) \right| & =\left| \frac{r\cdot \mathrm{ex}(n,F)}{n} - \frac{r\cdot \mathrm{ex}(n-m,F)}{n-m} \right| \\ & = \left| \frac{r}{n}\left(\mathrm{ex}(n,F)-\mathrm{ex}(n-m,F)\right) - \frac{rm}{n(n-m)}\mathrm{ex}(n-m,F) \right|\\ & \le \max\left\{ \frac{2mr^2}{n(n-m-r+1)},\frac{rm}{n(n-m)} \right\} \cdot \mathrm{ex}(n-m,F) \\ & \le \frac{2mr^2}{n(n-m-r+1)} \binom{n-m}{r} \le 4m \binom{n-m}{r-2}. \end{align*} $$
This completes the proof of Lemma 3.5.
The following lemma deals with a simple case of Theorem 3.1 in which the maximum degree of every r-graph
![]() $\mathcal {H}_i$
is bounded away from
$\mathcal {H}_i$
is bounded away from
![]() $\binom {n-1}{r-1}$
.
$\binom {n-1}{r-1}$
.
Lemma 3.6 Let F be a nondegenerate r-graph with m vertices. Suppose that
![]() $\mathrm {ex}(n,F)$
is g-smooth with
$\mathrm {ex}(n,F)$
is g-smooth with
![]() $g(n) \le \frac {1-\pi (F)}{8m}\binom {n}{r-1}$
for all sufficiently large n. Then there exists
$g(n) \le \frac {1-\pi (F)}{8m}\binom {n}{r-1}$
for all sufficiently large n. Then there exists
![]() $N_1$
such that the following holds for all integers
$N_1$
such that the following holds for all integers
![]() $n, t\in \mathbb {N}$
with
$n, t\in \mathbb {N}$
with
![]() $n\ge N_1$
and
$n\ge N_1$
and
![]() $t \le \frac {1-\pi (F)}{64rm^2} n$
.
$t \le \frac {1-\pi (F)}{64rm^2} n$
.
Suppose that
![]() $\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
is a collection of n-vertex r-graphs on the same vertex set V such that
$\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
is a collection of n-vertex r-graphs on the same vertex set V such that
hold for all
![]() $i\in [t+1]$
. Then
$i\in [t+1]$
. Then
![]() $\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
contains a rainbow F-matching.
$\left \{\mathcal {H}_1, \ldots , \mathcal {H}_{t+1}\right \}$
contains a rainbow F-matching.
Proof Given an integer
![]() $k \le t+1$
, we say a collection
$k \le t+1$
, we say a collection
![]() $\mathcal {C} = \{S_1, \ldots , S_{k}\}$
of pairwise disjoint m-subsets of V is F-rainbow if there exists an injection
$\mathcal {C} = \{S_1, \ldots , S_{k}\}$
of pairwise disjoint m-subsets of V is F-rainbow if there exists an injection
![]() $f \colon [k]\to [t+1]$
such that
$f \colon [k]\to [t+1]$
such that
![]() $F \subset \mathcal {H}_{f(i)}[S_i]$
for all
$F \subset \mathcal {H}_{f(i)}[S_i]$
for all
![]() $i\in [k]$
.
$i\in [k]$
.
Fix a maximal collection
![]() $\mathcal {C} = \{S_1, \ldots , S_{k}\}$
of pairwise disjoint m-subsets of V that is F-rainbow. If
$\mathcal {C} = \{S_1, \ldots , S_{k}\}$
of pairwise disjoint m-subsets of V that is F-rainbow. If
![]() $k = t+1$
, then we are done. So we may assume that
$k = t+1$
, then we are done. So we may assume that
![]() $k \le t$
. Without loss of generality, we may assume that
$k \le t$
. Without loss of generality, we may assume that
![]() $F \subset \mathcal {H}_i[S_i]$
for all
$F \subset \mathcal {H}_i[S_i]$
for all
![]() $i\in [k]$
(i.e., f is the identity map). Let
$i\in [k]$
(i.e., f is the identity map). Let
![]() $B = \bigcup _{i=1}^{k}S_i$
and let
$B = \bigcup _{i=1}^{k}S_i$
and let
![]() $b = |B| = mk$
.
$b = |B| = mk$
.
Let us count the number of edges in
![]() $\mathcal {H}_{k+1}$
. Observe that every copy of F in
$\mathcal {H}_{k+1}$
. Observe that every copy of F in
![]() $\mathcal {H}_{k+1}$
must contain a vertex from B, since otherwise, it would contradict the maximality of
$\mathcal {H}_{k+1}$
must contain a vertex from B, since otherwise, it would contradict the maximality of
![]() $\mathcal {C}$
. Therefore, the induced subgraph of
$\mathcal {C}$
. Therefore, the induced subgraph of
![]() $\mathcal {H}_{k+1}$
on
$\mathcal {H}_{k+1}$
on
![]() $V_0:= V\setminus B$
is F-free. Hence, by the maximum degree assumption, we obtain
$V_0:= V\setminus B$
is F-free. Hence, by the maximum degree assumption, we obtain
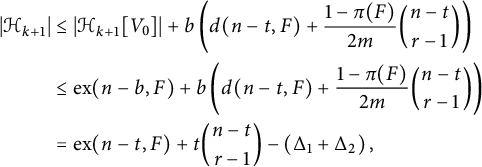 $$ \begin{align*} |\mathcal{H}_{k+1}| & \le |\mathcal{H}_{k+1}[V_0]| + b \left(d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} \right) \\ & \le \mathrm{ex}(n-b, F) + b \left(d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} \right) \\ & = \mathrm{ex}(n-t, F) + t \binom{n-t}{r-1} - \left(\Delta_1 + \Delta_2\right), \end{align*} $$
$$ \begin{align*} |\mathcal{H}_{k+1}| & \le |\mathcal{H}_{k+1}[V_0]| + b \left(d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} \right) \\ & \le \mathrm{ex}(n-b, F) + b \left(d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} \right) \\ & = \mathrm{ex}(n-t, F) + t \binom{n-t}{r-1} - \left(\Delta_1 + \Delta_2\right), \end{align*} $$
where
 $$ \begin{align*} \Delta_1 & := \mathrm{ex}(n-t, F)-\mathrm{ex}(n-b, F) - (b-t)d(n-t, F), \\ \Delta_2 & := t \left(\binom{n-t}{r-1} - d(n-t, F)\right) - b \frac{1-\pi(F)}{2m} \binom{n-t}{r-1}. \end{align*} $$
$$ \begin{align*} \Delta_1 & := \mathrm{ex}(n-t, F)-\mathrm{ex}(n-b, F) - (b-t)d(n-t, F), \\ \Delta_2 & := t \left(\binom{n-t}{r-1} - d(n-t, F)\right) - b \frac{1-\pi(F)}{2m} \binom{n-t}{r-1}. \end{align*} $$
Next, we will prove that
![]() $\Delta _1 + \Delta _2>0$
, which implies that
$\Delta _1 + \Delta _2>0$
, which implies that
![]() $|\mathcal {H}_{k+1}| < \mathrm {ex}(n-t, F) + t \binom {n-t}{r-1}$
contradicting our assumption.
$|\mathcal {H}_{k+1}| < \mathrm {ex}(n-t, F) + t \binom {n-t}{r-1}$
contradicting our assumption.
Since
![]() $n-t \ge N_1/2$
is sufficiently large and
$n-t \ge N_1/2$
is sufficiently large and
![]() $\lim _{n\to \infty }\mathrm {ex}(n-t,F)/\binom {n-t}{r} = \pi (F)$
, we have
$\lim _{n\to \infty }\mathrm {ex}(n-t,F)/\binom {n-t}{r} = \pi (F)$
, we have
![]() $\mathrm {ex}(n-t,F) \le \left (\pi (F)+ \frac {1-\pi (F)}{5}\right )\binom {n-t}{r}$
, and hence,
$\mathrm {ex}(n-t,F) \le \left (\pi (F)+ \frac {1-\pi (F)}{5}\right )\binom {n-t}{r}$
, and hence,
 $$ \begin{align*} d(n-t, F) = \frac{r\cdot \mathrm{ex}(n-t,F)}{n-t} \le \left(\pi(F)+ \frac{1-\pi(F)}{5}\right)\binom{n-t}{r-1}. \end{align*} $$
$$ \begin{align*} d(n-t, F) = \frac{r\cdot \mathrm{ex}(n-t,F)}{n-t} \le \left(\pi(F)+ \frac{1-\pi(F)}{5}\right)\binom{n-t}{r-1}. \end{align*} $$
Therefore,
 $$ \begin{align*} \Delta_2 & \ge t \left(1 - \left(\pi(F)+ \frac{1-\pi(F)}{5}\right)\right) \binom{n-t}{r-1} - mt \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} \\ & \ge \frac{1-\pi(F)}{4}\binom{n-t}{r-1} t. \end{align*} $$
$$ \begin{align*} \Delta_2 & \ge t \left(1 - \left(\pi(F)+ \frac{1-\pi(F)}{5}\right)\right) \binom{n-t}{r-1} - mt \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} \\ & \ge \frac{1-\pi(F)}{4}\binom{n-t}{r-1} t. \end{align*} $$
On the other hand, by Lemma 3.5, we have
Therefore, it follows from the Smoothness assumption and g is nondecreasing that
 $$ \begin{align*} \Delta_1 & = \sum_{i=1}^{b-t}\left(\mathrm{ex}(n-b+i, F) - \mathrm{ex}(n-b+i-1, F)\right) - (b-t)d(n-t,F) \\ & \overset{\text{Smoothness}}{\ge} \sum_{i=0}^{b-t-1}\left(d(n-b+i, F) - g(n-b+i+1)\right) - (b-t)d(n-t,F) \\ &\overset{\text{Nondecreasing}} {\ge} \sum_{i=0}^{b-t-1}\left(d(n-b+i, F) - d(n-t,F)\right) - (b-t)g(n-t) \\ & \overset{\text{Lemma~}3.5}{\ge} -\sum_{i=0}^{b-t-1}4(b-t-i)\binom{n-b+i}{r-2} - (b-t)g(n-t) \\ & \ge - 4m^2t^2 \binom{n-t-1}{r-2} - mt \cdot g(n-t) = - \frac{4(r-1)m^2t^2}{n-t} \binom{n-t}{r-1} - mt \cdot g(n-t). \end{align*} $$
$$ \begin{align*} \Delta_1 & = \sum_{i=1}^{b-t}\left(\mathrm{ex}(n-b+i, F) - \mathrm{ex}(n-b+i-1, F)\right) - (b-t)d(n-t,F) \\ & \overset{\text{Smoothness}}{\ge} \sum_{i=0}^{b-t-1}\left(d(n-b+i, F) - g(n-b+i+1)\right) - (b-t)d(n-t,F) \\ &\overset{\text{Nondecreasing}} {\ge} \sum_{i=0}^{b-t-1}\left(d(n-b+i, F) - d(n-t,F)\right) - (b-t)g(n-t) \\ & \overset{\text{Lemma~}3.5}{\ge} -\sum_{i=0}^{b-t-1}4(b-t-i)\binom{n-b+i}{r-2} - (b-t)g(n-t) \\ & \ge - 4m^2t^2 \binom{n-t-1}{r-2} - mt \cdot g(n-t) = - \frac{4(r-1)m^2t^2}{n-t} \binom{n-t}{r-1} - mt \cdot g(n-t). \end{align*} $$
Since
![]() $t \le \frac {1-\pi (F)}{64rm^2} n$
, we obtain
$t \le \frac {1-\pi (F)}{64rm^2} n$
, we obtain
![]() $\frac {4(r-1)m^2t^2}{n-t} < \frac {1-\pi (F)}{8} t$
. Together with
$\frac {4(r-1)m^2t^2}{n-t} < \frac {1-\pi (F)}{8} t$
. Together with
![]() $g(n-t) \le \frac {1-\pi (F)}{8m}\binom {n-t}{r-1}$
, we obtain
$g(n-t) \le \frac {1-\pi (F)}{8m}\binom {n-t}{r-1}$
, we obtain
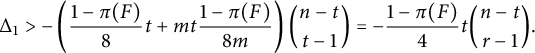 $$ \begin{align*} \Delta_1> -\left(\frac{1-\pi(F)}{8} t + m t \frac{1-\pi(F)}{8m}\right) \binom{n-t}{t-1} = - \frac{1-\pi(F)}{4} t \binom{n-t}{r-1}. \end{align*} $$
$$ \begin{align*} \Delta_1> -\left(\frac{1-\pi(F)}{8} t + m t \frac{1-\pi(F)}{8m}\right) \binom{n-t}{t-1} = - \frac{1-\pi(F)}{4} t \binom{n-t}{r-1}. \end{align*} $$
Therefore,
![]() $\Delta _1 + \Delta _2> 0$
. This finishes the proof of Lemma 3.6.
$\Delta _1 + \Delta _2> 0$
. This finishes the proof of Lemma 3.6.
3.2 Proof of Theorem 3.1
We prove Theorem 3.1 in this section. Let us prove Part (i) first.
Proof of Theorem 3.1 (i)
Fix a sufficiently large constant
![]() $N_0$
and suppose that
$N_0$
and suppose that
![]() ${n \ge N_0}$
. Let
${n \ge N_0}$
. Let
![]() $k \le t+1$
. We say a collection
$k \le t+1$
. We say a collection
![]() $L:= \{v_1, \ldots , v_k\}$
of vertices in V is heavy-rainbow if there exists an injection
$L:= \{v_1, \ldots , v_k\}$
of vertices in V is heavy-rainbow if there exists an injection
![]() $f \colon [k] \to [t+1]$
such that
$f \colon [k] \to [t+1]$
such that
Fix a maximal collection
![]() $L:= \{v_1, \ldots , v_k\}$
of vertices that is heavy-rainbow. Without loss of generality, we may assume that f (defined above) is the identity map.
$L:= \{v_1, \ldots , v_k\}$
of vertices that is heavy-rainbow. Without loss of generality, we may assume that f (defined above) is the identity map.
Let
![]() $V_0 = V \setminus L$
and
$V_0 = V \setminus L$
and
![]() $\mathcal {H}^{\prime }_{j} = \mathcal {H}_{j}[V_0]$
for all
$\mathcal {H}^{\prime }_{j} = \mathcal {H}_{j}[V_0]$
for all
![]() $j\in [k+1, t+1]$
. For every
$j\in [k+1, t+1]$
. For every
![]() $j\in [k+1, t+1]$
observe that there are at most
$j\in [k+1, t+1]$
observe that there are at most
![]() $\binom {n}{r}-\binom {n-k}{r}$
edges in
$\binom {n}{r}-\binom {n-k}{r}$
edges in
![]() $\mathcal {H}_j$
that have nonempty intersection with L. Hence,
$\mathcal {H}_j$
that have nonempty intersection with L. Hence,
 $$ \begin{align*} |\mathcal{H}^{\prime}_{j}| & \ge |\mathcal{H}_j| - \left(\binom{n}{r}-\binom{n-k}{r}\right) \\ & \ge \mathrm{ex}(n-t, F) + \binom{n}{r}-\binom{n-t}{r} - \left(\binom{n}{r}-\binom{n-k}{r}\right) \\ & = \mathrm{ex}((n-k)-(t-k), F) + \binom{n-k}{r} - \binom{(n-k)-(t-k)}{r}. \end{align*} $$
$$ \begin{align*} |\mathcal{H}^{\prime}_{j}| & \ge |\mathcal{H}_j| - \left(\binom{n}{r}-\binom{n-k}{r}\right) \\ & \ge \mathrm{ex}(n-t, F) + \binom{n}{r}-\binom{n-t}{r} - \left(\binom{n}{r}-\binom{n-k}{r}\right) \\ & = \mathrm{ex}((n-k)-(t-k), F) + \binom{n-k}{r} - \binom{(n-k)-(t-k)}{r}. \end{align*} $$
On the other hand, it follows from the maximality of L that
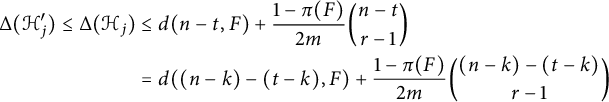 $$ \begin{align*} \Delta(\mathcal{H}^{\prime}_{j}) \le \Delta(\mathcal{H}_j) & \le d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} \\ & = d((n-k)-(t-k), F) + \frac{1-\pi(F)}{2m} \binom{(n-k)-(t-k)}{r-1} \end{align*} $$
$$ \begin{align*} \Delta(\mathcal{H}^{\prime}_{j}) \le \Delta(\mathcal{H}_j) & \le d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} \\ & = d((n-k)-(t-k), F) + \frac{1-\pi(F)}{2m} \binom{(n-k)-(t-k)}{r-1} \end{align*} $$
holds for all
![]() $j\in [k+1, t+1]$
. By assumption,
$j\in [k+1, t+1]$
. By assumption,
![]() $\frac {t-k}{n-k} \le \frac {t}{n} \le \frac {1-\pi (F)}{64rm^2}$
and
$\frac {t-k}{n-k} \le \frac {t}{n} \le \frac {1-\pi (F)}{64rm^2}$
and
![]() $n-k \ge n/2$
is sufficiently large, so it follows from Lemma 3.6 that there exists a collection
$n-k \ge n/2$
is sufficiently large, so it follows from Lemma 3.6 that there exists a collection
![]() $\mathcal {C} = \{S_{k+1}, \ldots , S_{t+1}\}$
of pairwise disjoint m-subsets of
$\mathcal {C} = \{S_{k+1}, \ldots , S_{t+1}\}$
of pairwise disjoint m-subsets of
![]() $V_0$
such that
$V_0$
such that
![]() $F \subset \mathcal {H}^{\prime }_{j}[S_j]$
for all
$F \subset \mathcal {H}^{\prime }_{j}[S_j]$
for all
![]() $j\in [k+1, t+1]$
.
$j\in [k+1, t+1]$
.
Next we will find a collection of rainbow copies of F from
![]() $\{\mathcal {H}_1, \ldots , \mathcal {H}_k\}$
.
$\{\mathcal {H}_1, \ldots , \mathcal {H}_k\}$
.
Claim 3.7 For every
![]() $i\in [k]$
and for every set
$i\in [k]$
and for every set
![]() $B_i \subset V \setminus \{v_i\}$
of size at most
$B_i \subset V \setminus \{v_i\}$
of size at most
![]() $2mt$
there exists a copy of F in
$2mt$
there exists a copy of F in
![]() $\mathcal {H}_i[V\setminus B_i]$
.
$\mathcal {H}_i[V\setminus B_i]$
.
Proof Fix
![]() $i \in [k]$
and fix a set
$i \in [k]$
and fix a set
![]() $B_i \subset V \setminus \{v_i\}$
of size at most
$B_i \subset V \setminus \{v_i\}$
of size at most
![]() $2mt$
. We may assume that
$2mt$
. We may assume that
![]() $|B_i| = 2mt$
. Let
$|B_i| = 2mt$
. Let
![]() $V_i = V\setminus B_i$
and
$V_i = V\setminus B_i$
and
![]() $n_i = |V_i| = n-2mt$
. Let
$n_i = |V_i| = n-2mt$
. Let
![]() $\mathcal {H}_i' = \mathcal {H}_i[V_i]$
. Since the number of edges in
$\mathcal {H}_i' = \mathcal {H}_i[V_i]$
. Since the number of edges in
![]() $\mathcal {H}_i$
containing
$\mathcal {H}_i$
containing
![]() $v_i$
that have nonempty intersection with
$v_i$
that have nonempty intersection with
![]() $B_i$
is at most
$B_i$
is at most
![]() $2mt \binom {n-1}{r-2}$
, we have
$2mt \binom {n-1}{r-2}$
, we have
 $$ \begin{align} d_{\mathcal{H}_i'}(v_i) & \ge d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} - 2mt \binom{n-1}{r-2} \notag\\ & \overset{\text{Lemma~}3.5}{\ge} d(n-2mt, F) - 2mt\binom{n-2mt}{r-2} + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} - 2mt \binom{n-1}{r-2} \notag \\ &> d(n-2mt, F) + \frac{1-\pi(F)}{4m} \binom{n-2mt}{r-1}, \end{align} $$
$$ \begin{align} d_{\mathcal{H}_i'}(v_i) & \ge d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} - 2mt \binom{n-1}{r-2} \notag\\ & \overset{\text{Lemma~}3.5}{\ge} d(n-2mt, F) - 2mt\binom{n-2mt}{r-2} + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1} - 2mt \binom{n-1}{r-2} \notag \\ &> d(n-2mt, F) + \frac{1-\pi(F)}{4m} \binom{n-2mt}{r-1}, \end{align} $$
where the last inequality holds because
![]() $t \le \frac {1-\pi (F)}{64rm^2}n$
and n is sufficiently large.
$t \le \frac {1-\pi (F)}{64rm^2}n$
and n is sufficiently large.
Similarly, we have
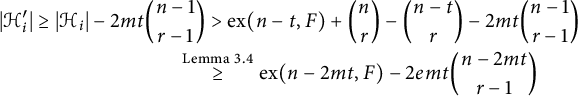 $$ \begin{align*} |\mathcal{H}_i'| \ge |\mathcal{H}_i| - 2mt\binom{n-1}{r-1} &> \mathrm{ex}(n-t,F)+ \binom{n}{r}-\binom{n-t}{r}-2mt\binom{n-1}{r-1} \\ &\hspace{-14pt}\overset{\text{Lemma~}3.4}{\ge} \mathrm{ex}(n-2mt,F) - 2emt\binom{n-2mt}{r-1} \end{align*} $$
$$ \begin{align*} |\mathcal{H}_i'| \ge |\mathcal{H}_i| - 2mt\binom{n-1}{r-1} &> \mathrm{ex}(n-t,F)+ \binom{n}{r}-\binom{n-t}{r}-2mt\binom{n-1}{r-1} \\ &\hspace{-14pt}\overset{\text{Lemma~}3.4}{\ge} \mathrm{ex}(n-2mt,F) - 2emt\binom{n-2mt}{r-1} \end{align*} $$
which, by the assumption
![]() $f(n-2mt) \ge 2emt\binom {n-2mt}{r-2}$
, implies that
$f(n-2mt) \ge 2emt\binom {n-2mt}{r-2}$
, implies that
 $$ \begin{align} d(\mathcal{H}_{i'}) = \frac{r\cdot |\mathcal{H}_i'|}{n-2mt} & \ge d(n-2mt,F) - 2emt\binom{n-2mt-1}{r-2} \notag \\ &> d(n-2mt,F) - f(n-2mt). \end{align} $$
$$ \begin{align} d(\mathcal{H}_{i'}) = \frac{r\cdot |\mathcal{H}_i'|}{n-2mt} & \ge d(n-2mt,F) - 2emt\binom{n-2mt-1}{r-2} \notag \\ &> d(n-2mt,F) - f(n-2mt). \end{align} $$
It follows from (3.2), (3.3), and the Boundedness assumption that
![]() $F \subset \mathcal {H}_{i}'$
.
$F \subset \mathcal {H}_{i}'$
.
Let
![]() $B = L \cup S_{k+1}\cup \cdots \cup S_{t+1}$
. Now we can repeatedly apply Claim 3.7 to find a collection of rainbow copies of F as follows. First, we let
$B = L \cup S_{k+1}\cup \cdots \cup S_{t+1}$
. Now we can repeatedly apply Claim 3.7 to find a collection of rainbow copies of F as follows. First, we let
![]() $B_1 = B\setminus \{v_1\}$
. Since
$B_1 = B\setminus \{v_1\}$
. Since
![]() $|B_1| = k-1+m(t+1-k) \le 2mt$
, Claim 3.7 applied to
$|B_1| = k-1+m(t+1-k) \le 2mt$
, Claim 3.7 applied to
![]() $v_1$
,
$v_1$
,
![]() $B_1$
, and
$B_1$
, and
![]() $\mathcal {H}_1$
yields an m-set
$\mathcal {H}_1$
yields an m-set
![]() $S_1 \subset V\setminus B_1$
such that
$S_1 \subset V\setminus B_1$
such that
![]() $F \subset \mathcal {H}_1[S_1]$
. Suppose that we have define
$F \subset \mathcal {H}_1[S_1]$
. Suppose that we have define
![]() $S_1, \ldots , S_i$
for some
$S_1, \ldots , S_i$
for some
![]() $i\in [k-1]$
such that
$i\in [k-1]$
such that
![]() $F \subset \mathcal {H}_j[S_j]$
holds for all
$F \subset \mathcal {H}_j[S_j]$
holds for all
![]() $j\le i$
. Then let
$j\le i$
. Then let
![]() $B_{i+1} = (B\cup S_1 \cup \cdots \cup S_i) \setminus \{v_{i+1}\}$
. Since
$B_{i+1} = (B\cup S_1 \cup \cdots \cup S_i) \setminus \{v_{i+1}\}$
. Since
![]() $|B_{i+1}| = k-1+m(t+1-k) + im \le 2 mt$
, Claim 3.7 applied to
$|B_{i+1}| = k-1+m(t+1-k) + im \le 2 mt$
, Claim 3.7 applied to
![]() $v_{i+1}$
,
$v_{i+1}$
,
![]() $B_{i+1}$
, and
$B_{i+1}$
, and
![]() $\mathcal {H}_{i+1}$
yields an m-set
$\mathcal {H}_{i+1}$
yields an m-set
![]() $S_{i+1} \subset V\setminus B_{i+1}$
such that
$S_{i+1} \subset V\setminus B_{i+1}$
such that
![]() $F \subset \mathcal {H}_{i+1}[S_{i+1}]$
. At the end of this process, we obtain a collection
$F \subset \mathcal {H}_{i+1}[S_{i+1}]$
. At the end of this process, we obtain a collection
![]() $\{S_1, \ldots , S_k\}$
of pairwise disjoint sets such that
$\{S_1, \ldots , S_k\}$
of pairwise disjoint sets such that
![]() $F \subset \mathcal {H}_{i}[S_{i}]$
holds for all
$F \subset \mathcal {H}_{i}[S_{i}]$
holds for all
![]() $i\in [k]$
. Since
$i\in [k]$
. Since
![]() $S_i \cap S_j = \emptyset $
for all
$S_i \cap S_j = \emptyset $
for all
![]() $i\in [k]$
and
$i\in [k]$
and
![]() $j\in [k+1, t+1]$
, the set
$j\in [k+1, t+1]$
, the set
![]() $\{S_1, \ldots , S_{t+1}\}$
yields a rainbow F-matching.
$\{S_1, \ldots , S_{t+1}\}$
yields a rainbow F-matching.
Before proving Part (ii) of Theorem 3.1, we need the simple corollary of Lemma 3.6.
Lemma 3.8 Let F be a nondegenerate r-graph with m vertices. Suppose that
![]() $\mathrm {ex}(n,F)$
is g-smooth with
$\mathrm {ex}(n,F)$
is g-smooth with
![]() $g(n) \le \frac {1-\pi (F)}{8m}\binom {n}{r-1}$
for all sufficiently large n. Then there exists
$g(n) \le \frac {1-\pi (F)}{8m}\binom {n}{r-1}$
for all sufficiently large n. Then there exists
![]() $N_1$
such that the following holds for all integers
$N_1$
such that the following holds for all integers
![]() $n, t\in \mathbb {N}$
with
$n, t\in \mathbb {N}$
with
![]() $n\ge N_1$
and
$n\ge N_1$
and
![]() $t \le \frac {1-\pi (F)}{64rm^2} n$
.
$t \le \frac {1-\pi (F)}{64rm^2} n$
.
Suppose that
![]() $\mathcal {H}$
is an n-vertex r-graph with
$\mathcal {H}$
is an n-vertex r-graph with
Then
Now we are ready to prove Part (ii).
Proof of Theorem 3.1 (ii)
Let
![]() $\mathcal {H}$
be an n-vertex r-graph with
$\mathcal {H}$
be an n-vertex r-graph with
![]() $\mathrm {ex}(n, (t+1)F)$
edges and
$\mathrm {ex}(n, (t+1)F)$
edges and
![]() $\nu (F, \mathcal {H}) < t+1$
. Note that Theorem 3.1 (i) already implies that
$\nu (F, \mathcal {H}) < t+1$
. Note that Theorem 3.1 (i) already implies that
![]() $\mathrm {ex}(n, (t+1)F) \le \binom {n}{r}-\binom {n-t}{r}+\mathrm {ex}(n-t, F)$
. So, it suffices to show that
$\mathrm {ex}(n, (t+1)F) \le \binom {n}{r}-\binom {n-t}{r}+\mathrm {ex}(n-t, F)$
. So, it suffices to show that
![]() $\mathcal {H}$
is isomorphic to
$\mathcal {H}$
is isomorphic to ![]() for some
for some
![]() $\mathcal {G} \in \mathrm {EX}(n-t,F)$
.
$\mathcal {G} \in \mathrm {EX}(n-t,F)$
.
Let
![]() $V = V(\mathcal {H})$
and define
$V = V(\mathcal {H})$
and define
 $$ \begin{align*} L := \left\{v\in V\colon d_{\mathcal{H}}(v) \ge d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1}\right\}. \end{align*} $$
$$ \begin{align*} L := \left\{v\in V\colon d_{\mathcal{H}}(v) \ge d(n-t, F) + \frac{1-\pi(F)}{2m} \binom{n-t}{r-1}\right\}. \end{align*} $$
A similar argument as in the proof of Claim 3.7 yields the following claim.
Claim 3.9 For every
![]() $v\in L$
and for every set
$v\in L$
and for every set
![]() $B\subset V\setminus \{v\}$
of size at most
$B\subset V\setminus \{v\}$
of size at most
![]() $2mt$
there exists a copy of F in
$2mt$
there exists a copy of F in
![]() $\mathcal {H}[V\setminus B]$
.
$\mathcal {H}[V\setminus B]$
.
Let
![]() $\ell =|L|$
. We have the following claim for
$\ell =|L|$
. We have the following claim for
![]() $\ell $
.
$\ell $
.
Claim 3.10 We have
![]() $\ell \le t$
.
$\ell \le t$
.
Proof Suppose to the contrary that
![]() $\ell \ge t+1$
. By taking a subset of L if necessary, we may assume that
$\ell \ge t+1$
. By taking a subset of L if necessary, we may assume that
![]() $\ell = t+1$
. Let us assume that
$\ell = t+1$
. Let us assume that
![]() $L = \{v_1, \ldots , v_{t+1}\}$
. We will repeatedly apply Claim 3.9 to find a collection
$L = \{v_1, \ldots , v_{t+1}\}$
. We will repeatedly apply Claim 3.9 to find a collection
![]() $\{S_1, \ldots , S_{t+1}\}$
of pairwise disjoint m-sets such that
$\{S_1, \ldots , S_{t+1}\}$
of pairwise disjoint m-sets such that
![]() $F\subset \mathcal {H}[S_i]$
for all
$F\subset \mathcal {H}[S_i]$
for all
![]() $i\in [t+1]$
as follows.
$i\in [t+1]$
as follows.
Let
![]() $B_1 = L\setminus \{v_1\}$
. Since
$B_1 = L\setminus \{v_1\}$
. Since
![]() $|B_1| \le 2mt$
, it follows from Claim 3.9 that there exists a set
$|B_1| \le 2mt$
, it follows from Claim 3.9 that there exists a set
![]() $S_1 \subset V\setminus B$
such that
$S_1 \subset V\setminus B$
such that
![]() $F\subset \mathcal {H}[S_1]$
. Now suppose that we have found pairwise disjoint m-sets
$F\subset \mathcal {H}[S_1]$
. Now suppose that we have found pairwise disjoint m-sets
![]() $S_1, \ldots , S_i$
for some
$S_1, \ldots , S_i$
for some
![]() $i \le t$
. Let
$i \le t$
. Let
![]() $B_{i+1} = \left (L\cup S_1 \cup \cdots \cup S_i\right ) \setminus \{v_i\}$
. It is clear that
$B_{i+1} = \left (L\cup S_1 \cup \cdots \cup S_i\right ) \setminus \{v_i\}$
. It is clear that
![]() $|B_{i+1}| \le 2mt$
. So it follows from Claim 3.9 that there exists a set
$|B_{i+1}| \le 2mt$
. So it follows from Claim 3.9 that there exists a set
![]() $S_{i+1} \subset V\setminus B$
such that
$S_{i+1} \subset V\setminus B$
such that
![]() $F\subset \mathcal {H}[S_{i+1}]$
. Repeat this process for
$F\subset \mathcal {H}[S_{i+1}]$
. Repeat this process for
![]() $t+1$
times, we find the collection
$t+1$
times, we find the collection
![]() $\{S_1, \ldots , S_{t+1}\}$
that satisfies the assertion. However, this contradicts the assumption that
$\{S_1, \ldots , S_{t+1}\}$
that satisfies the assertion. However, this contradicts the assumption that
![]() $\nu (F, \mathcal {H}) < t+1$
.
$\nu (F, \mathcal {H}) < t+1$
.
Let
![]() $V_0 = V\setminus L$
and
$V_0 = V\setminus L$
and
![]() $\mathcal {H}_0 = \mathcal {H}[V_0]$
. The following claim follows from a similar argument as in the last paragraph of the proof of Theorem 3.1.
$\mathcal {H}_0 = \mathcal {H}[V_0]$
. The following claim follows from a similar argument as in the last paragraph of the proof of Theorem 3.1.
Claim 3.11 We have
![]() $\nu (F, \mathcal {H}_0) < t-\ell +1$
.
$\nu (F, \mathcal {H}_0) < t-\ell +1$
.
If
![]() $\ell =t$
, then Claim 3.11 implies that
$\ell =t$
, then Claim 3.11 implies that
![]() $\mathcal {H}_0$
is F-free. Therefore, it follows from
$\mathcal {H}_0$
is F-free. Therefore, it follows from
that
![]() $\mathcal {H}_0 \in \mathrm {EX}(n-t, F)$
and
$\mathcal {H}_0 \in \mathrm {EX}(n-t, F)$
and
![]() $d(v) = \binom {n-1}{r-1}$
for all
$d(v) = \binom {n-1}{r-1}$
for all
![]() $v\in L$
, which implies that
$v\in L$
, which implies that ![]() for some
for some
![]() $\mathcal {G} \in \mathrm {EX}(n-t, F)$
.
$\mathcal {G} \in \mathrm {EX}(n-t, F)$
.
If
![]() $\ell \le t-1$
, then it follows from
$\ell \le t-1$
, then it follows from
![]() $\Delta (\mathcal {H}_0) \le d(n-t, F) + \frac {1-\pi (F)}{2m} \binom {n-t}{r-1}$
,
$\Delta (\mathcal {H}_0) \le d(n-t, F) + \frac {1-\pi (F)}{2m} \binom {n-t}{r-1}$
,
![]() $\nu (F, \mathcal {H}_0) < t-\ell +1$
, and Lemma 3.8 that
$\nu (F, \mathcal {H}_0) < t-\ell +1$
, and Lemma 3.8 that
Consequently,
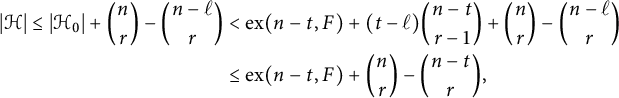 $$ \begin{align*} |\mathcal{H}| \le |\mathcal{H}_0| + \binom{n}{r}-\binom{n-\ell}{r} & < \mathrm{ex}(n-t, F) + (t-\ell)\binom{n-t}{r-1} + \binom{n}{r}-\binom{n-\ell}{r} \\ & \le \mathrm{ex}(n-t, F) + \binom{n}{r}-\binom{n-t}{r}, \end{align*} $$
$$ \begin{align*} |\mathcal{H}| \le |\mathcal{H}_0| + \binom{n}{r}-\binom{n-\ell}{r} & < \mathrm{ex}(n-t, F) + (t-\ell)\binom{n-t}{r-1} + \binom{n}{r}-\binom{n-\ell}{r} \\ & \le \mathrm{ex}(n-t, F) + \binom{n}{r}-\binom{n-t}{r}, \end{align*} $$
a contradiction.
4 Proofs of Theorems 1.7 and 1.9
In this section, we prove Theorems 1.7 and 1.9. Before that, let us introduce some definitions and prove some preliminary results.
4.1 Preliminaries
The following fact concerning
![]() $\delta (n,F)$
for all hypergraphs F.
$\delta (n,F)$
for all hypergraphs F.
Fact 4.1 Let F be an r-graph and
![]() $n\ge 1$
be an integer. Then every maximum n-vertex F-free r-graph
$n\ge 1$
be an integer. Then every maximum n-vertex F-free r-graph
![]() $\mathcal {H}$
satisfies
$\mathcal {H}$
satisfies
![]() $\delta (\mathcal {H}) \ge \delta (n,F)$
. In particular,
$\delta (\mathcal {H}) \ge \delta (n,F)$
. In particular,
![]() $d(n,F) \ge \delta (n,F)$
.
$d(n,F) \ge \delta (n,F)$
.
Proof Let
![]() $v\in V(\mathcal {H})$
be a vertex with minimum degree and let
$v\in V(\mathcal {H})$
be a vertex with minimum degree and let
![]() $\mathcal {H}^{\prime }$
be the induced subgraph of
$\mathcal {H}^{\prime }$
be the induced subgraph of
![]() $\mathcal {H}$
on
$\mathcal {H}$
on
![]() $V(\mathcal {H})\setminus \{v\}$
. Since
$V(\mathcal {H})\setminus \{v\}$
. Since
![]() $\mathcal {H}^{\prime }$
is an
$\mathcal {H}^{\prime }$
is an
![]() $(n-1)$
-vertex F-free r-graph, we have
$(n-1)$
-vertex F-free r-graph, we have
![]() $|\mathcal {H}^{\prime }| \le \mathrm {ex}(n-1, F)$
. On the other hand, since
$|\mathcal {H}^{\prime }| \le \mathrm {ex}(n-1, F)$
. On the other hand, since
![]() $\mathcal {H}$
is a maximum n-vertex F-free r-graph, we have
$\mathcal {H}$
is a maximum n-vertex F-free r-graph, we have
![]() $\mathrm {ex}(n,F) = |\mathcal {H}|$
. Therefore,
$\mathrm {ex}(n,F) = |\mathcal {H}|$
. Therefore,
which proves Fact 4.1.
For Turán pairs
![]() $(F,P)$
we have the following fact which provides a lower bound for
$(F,P)$
we have the following fact which provides a lower bound for
![]() $\delta (n,F)$
.
$\delta (n,F)$
.
Fact 4.2 Suppose that
![]() $(F,P)$
is a Turán pair and
$(F,P)$
is a Turán pair and
![]() $\mathcal {H}$
is a maximum F-free r-graph on
$\mathcal {H}$
is a maximum F-free r-graph on
![]() $n-1$
vertices. Then
$n-1$
vertices. Then
![]() $\delta (n,F) \ge \Delta (\mathcal {H})$
. In particular,
$\delta (n,F) \ge \Delta (\mathcal {H})$
. In particular,
![]() $\delta (n,F) \ge d(n-1,F)$
.
$\delta (n,F) \ge d(n-1,F)$
.
Proof First, notice that
![]() $|\mathcal {H}| = \mathrm {ex}(n-1, F)$
. On the other hand, it follows from the definition of Turán pair that
$|\mathcal {H}| = \mathrm {ex}(n-1, F)$
. On the other hand, it follows from the definition of Turán pair that
![]() $\mathcal {H}$
is an
$\mathcal {H}$
is an
![]() $(n-1)$
-vertex P-construction. Let
$(n-1)$
-vertex P-construction. Let
![]() $\tilde {\mathcal {H}}$
be an n-vertex P-construction obtained from
$\tilde {\mathcal {H}}$
be an n-vertex P-construction obtained from
![]() $\mathcal {H}$
by duplicating a vertex
$\mathcal {H}$
by duplicating a vertex
![]() $v\in V(\mathcal {H})$
with maximum degree. In other words,
$v\in V(\mathcal {H})$
with maximum degree. In other words,
![]() $\tilde {\mathcal {H}}$
is obtained from
$\tilde {\mathcal {H}}$
is obtained from
![]() $\mathcal {H}$
by adding a new vertex u and adding all edges in
$\mathcal {H}$
by adding a new vertex u and adding all edges in
![]() $\left \{\{u\} \cup S \colon S \in L_{\mathcal {H}}(v)\right \}$
. It is clear that
$\left \{\{u\} \cup S \colon S \in L_{\mathcal {H}}(v)\right \}$
. It is clear that
![]() $\tilde {\mathcal {H}}$
is an n-vertex P-construction, and hence,
$\tilde {\mathcal {H}}$
is an n-vertex P-construction, and hence,
![]() $\tilde {\mathcal {H}}$
is F-free. So
$\tilde {\mathcal {H}}$
is F-free. So
![]() $|\tilde {\mathcal {H}}| \le \mathrm {ex}(n,F)$
. It follows that
$|\tilde {\mathcal {H}}| \le \mathrm {ex}(n,F)$
. It follows that
which proves Fact 4.2.
The following result can be derived with a minor modification to the proof of [Reference Liu, Mubayi and Reiher50, Lemma 4.2] (see Section 1 for details).
Fact 4.3 Let F be an r-graph and let
![]() $\mathcal {H}$
be an n-vertex F-free r-graph. If n is large,
$\mathcal {H}$
be an n-vertex F-free r-graph. If n is large,
![]() $\varepsilon>0$
is small, and
$\varepsilon>0$
is small, and
![]() $|\mathcal {H}| \ge \left (\pi (F) - \varepsilon \right )\binom {n}{r}$
, then
$|\mathcal {H}| \ge \left (\pi (F) - \varepsilon \right )\binom {n}{r}$
, then
-
(a) the set
has size at most $$ \begin{align*} Z_{\varepsilon}(\mathcal{H}) := \left\{v\in V(\mathcal{H}) \colon d_{\mathcal{H}}(v) \le \left(\pi(F)-r\varepsilon^{1/2}\right)\binom{n-1}{r-1}\right\} \end{align*} $$
$$ \begin{align*} Z_{\varepsilon}(\mathcal{H}) := \left\{v\in V(\mathcal{H}) \colon d_{\mathcal{H}}(v) \le \left(\pi(F)-r\varepsilon^{1/2}\right)\binom{n-1}{r-1}\right\} \end{align*} $$
 $\varepsilon ^{1/2}n$
, and
$\varepsilon ^{1/2}n$
, and
-
(b) the induced subgraph
 $\mathcal {H}^{\prime }$
of
$\mathcal {H}^{\prime }$
of
 $\mathcal {H}$
on
$\mathcal {H}$
on
 $V(\mathcal {H})\setminus Z_{\varepsilon }(\mathcal {H})$
satisfies
$V(\mathcal {H})\setminus Z_{\varepsilon }(\mathcal {H})$
satisfies
 $\delta (\mathcal {H}^{\prime }) \ge \left (\pi (F)-2r\varepsilon ^{1/2}\right )\binom {n-1}{r-1}$
.
$\delta (\mathcal {H}^{\prime }) \ge \left (\pi (F)-2r\varepsilon ^{1/2}\right )\binom {n-1}{r-1}$
.
4.2 Proofs of Theorems 1.7 and 1.9
We prove Theorem 1.7 first.
Proof of Theorem 1.7
Fix an integer
![]() $n \ge 1$
. Then
$n \ge 1$
. Then
 $$ \begin{align*} |\delta(n,F) - d(n-1,F)| &\overset{\text{Fact~4.2}}{=} \delta(n,F) - d(n-1,F) \\ &\overset{\text{Fact~}4.1}{\le} d(n,F) - d(n-1,F) \overset{\text{Lemma~}3.5}{\le} 4\binom{n-1}{r-2}, \end{align*} $$
$$ \begin{align*} |\delta(n,F) - d(n-1,F)| &\overset{\text{Fact~4.2}}{=} \delta(n,F) - d(n-1,F) \\ &\overset{\text{Fact~}4.1}{\le} d(n,F) - d(n-1,F) \overset{\text{Lemma~}3.5}{\le} 4\binom{n-1}{r-2}, \end{align*} $$
which proves Theorem 1.7.
Next we prove Theorem 1.9.
Proof of Theorem 1.9
Fix constants
![]() $0 < \varepsilon \ll \varepsilon _1 \ll 1$
and let
$0 < \varepsilon \ll \varepsilon _1 \ll 1$
and let
![]() $n \in \mathbb {N}$
be sufficiently large. Suppose to the contrary that there exists an n-vertex F-free r-graph
$n \in \mathbb {N}$
be sufficiently large. Suppose to the contrary that there exists an n-vertex F-free r-graph
![]() $\mathcal {H}$
with
$\mathcal {H}$
with
![]() $d(\mathcal {H}) \ge d(n,F) - \varepsilon \binom {n-1}{r-1}$
and
$d(\mathcal {H}) \ge d(n,F) - \varepsilon \binom {n-1}{r-1}$
and
![]() $\Delta (\mathcal {H}) \ge d(n,F)+ \frac {1-\pi (F)}{8m}\binom {n-1}{r-1}$
. Let
$\Delta (\mathcal {H}) \ge d(n,F)+ \frac {1-\pi (F)}{8m}\binom {n-1}{r-1}$
. Let
![]() $V = V(\mathcal {H})$
. Fix a vertex
$V = V(\mathcal {H})$
. Fix a vertex
![]() $v\in V$
with
$v\in V$
with
![]() $d_{\mathcal {H}}(v) = \Delta (\mathcal {H})$
. Let
$d_{\mathcal {H}}(v) = \Delta (\mathcal {H})$
. Let
![]() $V_0 = V\setminus \{v\}$
and
$V_0 = V\setminus \{v\}$
and
![]() $\mathcal {H}_0 = \mathcal {H}[V_0]$
. Since
$\mathcal {H}_0 = \mathcal {H}[V_0]$
. Since
it follows from the edge-stability of F that
![]() $\mathcal {H}_0$
contains a subgraph
$\mathcal {H}_0$
contains a subgraph
![]() $\mathcal {H}_1$
with at least
$\mathcal {H}_1$
with at least
![]() $\mathrm {ex}(n,F) - \varepsilon _1\binom {n}{r} \ge \left (\pi (F)-\varepsilon _1\right )\binom {n}{r}$
edges, and moreover,
$\mathrm {ex}(n,F) - \varepsilon _1\binom {n}{r} \ge \left (\pi (F)-\varepsilon _1\right )\binom {n}{r}$
edges, and moreover,
![]() $\mathcal {H}_1$
is a P-subconstruction.
$\mathcal {H}_1$
is a P-subconstruction.
It follows from Fact 4.3 that the set
has size at most
![]() $\varepsilon _1^{1/2} n$
, and moreover, the r-graph
$\varepsilon _1^{1/2} n$
, and moreover, the r-graph
![]() $\mathcal {H}_2 := \mathcal {H}_1[V_0\setminus Z]$
satisfies
$\mathcal {H}_2 := \mathcal {H}_1[V_0\setminus Z]$
satisfies
![]() $\delta (\mathcal {H}_2) \ge \left (\pi (F)-2r\varepsilon _1^{1/2}\right )\binom {n-1}{r-1}$
. Note that
$\delta (\mathcal {H}_2) \ge \left (\pi (F)-2r\varepsilon _1^{1/2}\right )\binom {n-1}{r-1}$
. Note that
![]() $\mathcal {H}_2 \subset \mathcal {H}_1$
is also a P-subconstruction.
$\mathcal {H}_2 \subset \mathcal {H}_1$
is also a P-subconstruction.
Define
![]() $\mathcal {H}_3 := \mathcal {H}_2 \cup \left \{e \in \mathcal {H}[V\setminus Z] \colon v\in e\right \}$
. Since
$\mathcal {H}_3 := \mathcal {H}_2 \cup \left \{e \in \mathcal {H}[V\setminus Z] \colon v\in e\right \}$
. Since
![]() $|Z| \le \varepsilon _1^{1/2}n \le \frac {1-\pi (F)}{72m}\frac {n}{r}$
, we have
$|Z| \le \varepsilon _1^{1/2}n \le \frac {1-\pi (F)}{72m}\frac {n}{r}$
, we have
 $$ \begin{align*} d_{\mathcal{H}_3}(v) \ge d_{\mathcal{H}}(v) - |Z|\binom{n-2}{r-2} & \ge d(n,F)+ \frac{1-\pi(F)}{8m}\binom{n-1}{r-1} - \frac{1-\pi(F)}{72m}\frac{n}{r}\binom{n-2}{r-2} \\ & \ge d(n,F)+ \frac{1-\pi(F)}{8m}\binom{n-1}{r-1} - \frac{1-\pi(F)}{72m}\binom{n-1}{r-1} \\ & \ge \left(\pi(F) + \frac{1-\pi(F)}{9m}\right) \binom{n-1}{r-1}. \end{align*} $$
$$ \begin{align*} d_{\mathcal{H}_3}(v) \ge d_{\mathcal{H}}(v) - |Z|\binom{n-2}{r-2} & \ge d(n,F)+ \frac{1-\pi(F)}{8m}\binom{n-1}{r-1} - \frac{1-\pi(F)}{72m}\frac{n}{r}\binom{n-2}{r-2} \\ & \ge d(n,F)+ \frac{1-\pi(F)}{8m}\binom{n-1}{r-1} - \frac{1-\pi(F)}{72m}\binom{n-1}{r-1} \\ & \ge \left(\pi(F) + \frac{1-\pi(F)}{9m}\right) \binom{n-1}{r-1}. \end{align*} $$
Let
![]() $n' = |V\setminus Z|$
. Note that
$n' = |V\setminus Z|$
. Note that
![]() $\mathcal {H}_3$
is an F-free r-graph on
$\mathcal {H}_3$
is an F-free r-graph on
![]() $n'$
vertices with
$n'$
vertices with
![]() $\delta (\mathcal {H}_3) \ge \delta (\mathcal {H}_2) \ge \left (\pi (F) - 2r \varepsilon _1^{1/2}\right )\binom {n-1}{r-1}$
, and
$\delta (\mathcal {H}_3) \ge \delta (\mathcal {H}_2) \ge \left (\pi (F) - 2r \varepsilon _1^{1/2}\right )\binom {n-1}{r-1}$
, and
![]() $v\in V(\mathcal {H}_3)$
is a vertex such that
$v\in V(\mathcal {H}_3)$
is a vertex such that
![]() $\mathcal {H}_3 - v = \mathcal {H}_2$
is a P-subconstruction. However, this contradicts the weak vertex-extendability of F since
$\mathcal {H}_3 - v = \mathcal {H}_2$
is a P-subconstruction. However, this contradicts the weak vertex-extendability of F since
![]() $\varepsilon _1$
is sufficiently small and
$\varepsilon _1$
is sufficiently small and
![]() $d_{\mathcal {H}_3}(v) \ge \left (\pi (F) + \frac {1-\pi (F)}{9m}\right ) \binom {n-1}{r-1}$
.
$d_{\mathcal {H}_3}(v) \ge \left (\pi (F) + \frac {1-\pi (F)}{9m}\right ) \binom {n-1}{r-1}$
.
5 Proof of Theorem 2.13
The edge-stability of
![]() $\mathbb {F}_{3,2}$
was already proved in [Reference Füredi, Pikhurko and Simonovits28, Theorem 2.2], so by Theorems 1.5, 1.7, and 1.9, to prove Theorem 2.13 it suffices to prove the following result.
$\mathbb {F}_{3,2}$
was already proved in [Reference Füredi, Pikhurko and Simonovits28, Theorem 2.2], so by Theorems 1.5, 1.7, and 1.9, to prove Theorem 2.13 it suffices to prove the following result.
Theorem 5.1 The
![]() $3$
-graph
$3$
-graph
![]() $\mathbb {F}_{3,2}$
is weakly vertex-extendable with respect to the pattern
$\mathbb {F}_{3,2}$
is weakly vertex-extendable with respect to the pattern
![]() $S_3 :=\left (2, \{1,2,2\}\right )$
.
$S_3 :=\left (2, \{1,2,2\}\right )$
.
Proof Fix
![]() $\delta>0$
. Let n be sufficiently large and
$\delta>0$
. Let n be sufficiently large and
![]() $\zeta>0$
be sufficiently small. Let
$\zeta>0$
be sufficiently small. Let
![]() $\mathcal {H}$
be an n-vertex
$\mathcal {H}$
be an n-vertex
![]() $\mathbb {F}_{3,2}$
-free
$\mathbb {F}_{3,2}$
-free
![]() $3$
-graph with
$3$
-graph with
![]() $\delta (\mathcal {H}) \ge \left (\frac {4}{9}-\zeta \right )\binom {n-1}{2}$
. Suppose that
$\delta (\mathcal {H}) \ge \left (\frac {4}{9}-\zeta \right )\binom {n-1}{2}$
. Suppose that
![]() $v\in V$
is a vertex such that
$v\in V$
is a vertex such that
![]() $\mathcal {H}_0 := \mathcal {H}-v$
is an
$\mathcal {H}_0 := \mathcal {H}-v$
is an
![]() $S_3$
-subconstruction (i.e., semibipartite). It suffices to show that
$S_3$
-subconstruction (i.e., semibipartite). It suffices to show that
![]() $d_{\mathcal {H}}(v) \le \left (\frac {4}{9}+\delta \right )\binom {n-1}{2}$
.
$d_{\mathcal {H}}(v) \le \left (\frac {4}{9}+\delta \right )\binom {n-1}{2}$
.
Suppose to the contrary that
![]() $d_{\mathcal {H}}(v)> \left (\frac {4}{9}+\delta \right )\binom {n-1}{2}$
. Let
$d_{\mathcal {H}}(v)> \left (\frac {4}{9}+\delta \right )\binom {n-1}{2}$
. Let
![]() $V_1 \cup V_2$
be a bipartition of
$V_1 \cup V_2$
be a bipartition of
![]() $V_0 := V\setminus \{v\}$
such that every edge in
$V_0 := V\setminus \{v\}$
such that every edge in
![]() $\mathcal {H}_0$
contains exactly one vertex from
$\mathcal {H}_0$
contains exactly one vertex from
![]() $V_1$
. Since
$V_1$
. Since
![]() $|\mathcal {H}_0| \ge \frac {3}{n}\delta (\mathcal {H}) \ge \left (\frac {4}{9}-\zeta \right )\binom {n}{3}$
, it follows from some simple calculations (see, e.g., [Reference Füredi, Pikhurko and Simonovits28, Theorem 2.2(ii)]) that
$|\mathcal {H}_0| \ge \frac {3}{n}\delta (\mathcal {H}) \ge \left (\frac {4}{9}-\zeta \right )\binom {n}{3}$
, it follows from some simple calculations (see, e.g., [Reference Füredi, Pikhurko and Simonovits28, Theorem 2.2(ii)]) that
Recall that the link of a vertex
![]() $u\in V(\mathcal {H})$
is defined as
$u\in V(\mathcal {H})$
is defined as
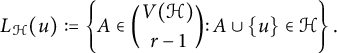 $$ \begin{align*} L_{\mathcal{H}}(u) :=\left\{A \in \binom{V(\mathcal{H})}{r-1}\colon A \cup \{u\}\in \mathcal{H}\right\}. \end{align*} $$
$$ \begin{align*} L_{\mathcal{H}}(u) :=\left\{A \in \binom{V(\mathcal{H})}{r-1}\colon A \cup \{u\}\in \mathcal{H}\right\}. \end{align*} $$
Let
![]() $L = L_{\mathcal {H}}(v)$
for simplicity and let
$L = L_{\mathcal {H}}(v)$
for simplicity and let
Here, we abuse the use of notation by letting
![]() $V_1\times V_2$
denote the edge set of the complete bipartite graph with parts
$V_1\times V_2$
denote the edge set of the complete bipartite graph with parts
![]() $V_1$
and
$V_1$
and
![]() $V_2$
.
$V_2$
.
Claim 5.2 We have
![]() $|L_2| \ge \frac {\delta }{8}n^2$
.
$|L_2| \ge \frac {\delta }{8}n^2$
.
Proof Suppose to the contrary that
![]() $|L_{2}| \le \delta n^2/8$
. Then it follows from the inequality
$|L_{2}| \le \delta n^2/8$
. Then it follows from the inequality
 $$ \begin{align*} \sum_{v'\in V_1}d_{L}(v') = 2|L_1|+|L_{1,2}| \ge |L| - |L_2| \ge \left(\frac{4}{9}+\delta\right)\binom{n-1}{2} - \frac{\delta}{8}n^2 \ge \left(\frac{2}{9}+\frac{\delta}{4}\right)n^2 \end{align*} $$
$$ \begin{align*} \sum_{v'\in V_1}d_{L}(v') = 2|L_1|+|L_{1,2}| \ge |L| - |L_2| \ge \left(\frac{4}{9}+\delta\right)\binom{n-1}{2} - \frac{\delta}{8}n^2 \ge \left(\frac{2}{9}+\frac{\delta}{4}\right)n^2 \end{align*} $$
that there exists a vertex
![]() $w\in V_1$
with
$w\in V_1$
with
 $$ \begin{align*} d_{L}(w) \ge \frac{\left(\frac{2}{9}+\frac{\delta}{4}\right)n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} \ge \left(\frac{2}{3}+\frac{\delta}{8}\right)n. \end{align*} $$
$$ \begin{align*} d_{L}(w) \ge \frac{\left(\frac{2}{9}+\frac{\delta}{4}\right)n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} \ge \left(\frac{2}{3}+\frac{\delta}{8}\right)n. \end{align*} $$
Therefore, by (5.1), we have
Fix a vertex
![]() $u\in N_{L}(w) \cap V_1$
and let
$u\in N_{L}(w) \cap V_1$
and let
![]() $V_2' = N_{L}(w) \cap V_2$
. Since
$V_2' = N_{L}(w) \cap V_2$
. Since
 $$ \begin{align} \binom{|V_2|}{2} - d_{\mathcal{H}_0}(u) \le \binom{\left(\frac{2}{3}+\zeta^{1/2}\right)n}{2} - \left(\frac{4}{9}-2\zeta\right)\binom{n-1}{2} < \binom{\delta n/16}{2}, \end{align} $$
$$ \begin{align} \binom{|V_2|}{2} - d_{\mathcal{H}_0}(u) \le \binom{\left(\frac{2}{3}+\zeta^{1/2}\right)n}{2} - \left(\frac{4}{9}-2\zeta\right)\binom{n-1}{2} < \binom{\delta n/16}{2}, \end{align} $$
there exists an edge
![]() $ab\in L_{\mathcal {H}}(u)\cap \binom {V_2'}{2}$
. However, this implies that
$ab\in L_{\mathcal {H}}(u)\cap \binom {V_2'}{2}$
. However, this implies that
![]() $\mathbb {F}_{3,2} \subset \mathcal {H}[\{v,u,w,a,b\}]$
(see Figure 8), a contradiction.
$\mathbb {F}_{3,2} \subset \mathcal {H}[\{v,u,w,a,b\}]$
(see Figure 8), a contradiction.
Claim 5.3 We have
![]() $L_1 = \emptyset $
.
$L_1 = \emptyset $
.
Proof Suppose to the contrary that there exists an edge
![]() $uw \in L_1$
. Note that
$uw \in L_1$
. Note that
![]() $|L_{2}| \ge \delta n^2/8$
from Claim 5.2. Choosing uniformly at random a pair
$|L_{2}| \ge \delta n^2/8$
from Claim 5.2. Choosing uniformly at random a pair
![]() $\{a,b\}$
from
$\{a,b\}$
from
![]() $\binom {V_2}{2}$
, we obtain
$\binom {V_2}{2}$
, we obtain
 $$ \begin{align*} \min\left\{\mathbb{P}\left[ab\in L_{\mathcal{H}}(u)\right], \mathbb{P}\left[ab\in L_{\mathcal{H}}(w)\right] \right\} \ge \frac{\delta(\mathcal{H}_0)}{\binom{|V_2|}{2}}> \frac{\left(\frac{4}{9}-2\zeta\right)\binom{n-1}{2}}{\binom{\left(\frac{2}{3}+\zeta^{1/2}\right)n}{2}} > 1- 10\zeta^{1/2}, \end{align*} $$
$$ \begin{align*} \min\left\{\mathbb{P}\left[ab\in L_{\mathcal{H}}(u)\right], \mathbb{P}\left[ab\in L_{\mathcal{H}}(w)\right] \right\} \ge \frac{\delta(\mathcal{H}_0)}{\binom{|V_2|}{2}}> \frac{\left(\frac{4}{9}-2\zeta\right)\binom{n-1}{2}}{\binom{\left(\frac{2}{3}+\zeta^{1/2}\right)n}{2}} > 1- 10\zeta^{1/2}, \end{align*} $$
and
 $$ \begin{align*} \mathbb{P}\left[ab\in L_2\right] = \frac{|L_2|}{\binom{|V_2|}{2}}> \frac{\delta n^2/8}{\binom{\left(\frac{2}{3}+\zeta^{1/2}\right)n}{2}} > \frac{\delta}{8}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left[ab\in L_2\right] = \frac{|L_2|}{\binom{|V_2|}{2}}> \frac{\delta n^2/8}{\binom{\left(\frac{2}{3}+\zeta^{1/2}\right)n}{2}} > \frac{\delta}{8}. \end{align*} $$
So it follows from the Union Bound that
Hence, there exists an edge
![]() $ab\in L_2 \cap L_{\mathcal {H}}(u) \cap L_{\mathcal {H}}(w)$
. However, this implies that
$ab\in L_2 \cap L_{\mathcal {H}}(u) \cap L_{\mathcal {H}}(w)$
. However, this implies that
![]() $\mathbb {F}_{3,2} \subset \mathcal {H}[\{v,u,w,a,b\}]$
(see Figure 8), a contradiction.
$\mathbb {F}_{3,2} \subset \mathcal {H}[\{v,u,w,a,b\}]$
(see Figure 8), a contradiction.
Let us define
It follows from
 $$ \begin{align*} \left(\frac{1}{3}+\zeta^{1/2}\right)n |U_1| \ge \sum_{v'\in U_1}|N_{L}(v') \cap V_1| \ge |L_{1,2}| - \frac{\delta}{16}n |V_2\setminus U_1| \ge |L_{1,2}| - \frac{\delta}{16}n^2 \end{align*} $$
$$ \begin{align*} \left(\frac{1}{3}+\zeta^{1/2}\right)n |U_1| \ge \sum_{v'\in U_1}|N_{L}(v') \cap V_1| \ge |L_{1,2}| - \frac{\delta}{16}n |V_2\setminus U_1| \ge |L_{1,2}| - \frac{\delta}{16}n^2 \end{align*} $$
and
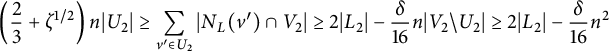 $$ \begin{align*} \left(\frac{2}{3}+\zeta^{1/2}\right)n |U_2| \ge \sum_{v'\in U_2}|N_{L}(v') \cap V_2| \ge 2|L_{2}| - \frac{\delta}{16}n |V_2\setminus U_2| \ge 2|L_{2}| - \frac{\delta}{16}n^2 \end{align*} $$
$$ \begin{align*} \left(\frac{2}{3}+\zeta^{1/2}\right)n |U_2| \ge \sum_{v'\in U_2}|N_{L}(v') \cap V_2| \ge 2|L_{2}| - \frac{\delta}{16}n |V_2\setminus U_2| \ge 2|L_{2}| - \frac{\delta}{16}n^2 \end{align*} $$
that
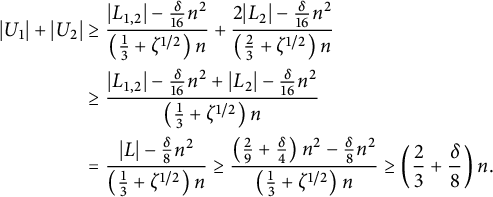 $$ \begin{align*} |U_1|+|U_2| & \ge \frac{|L_{1,2}| - \frac{\delta}{16}n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} + \frac{2|L_{2}| - \frac{\delta}{16}n^2}{\left(\frac{2}{3}+\zeta^{1/2}\right)n} \\ & \ge \frac{|L_{1,2}| - \frac{\delta}{16}n^2 + |L_{2}| - \frac{\delta}{16}n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} \\ & = \frac{|L| - \frac{\delta}{8}n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} \ge \frac{\left(\frac{2}{9}+\frac{\delta}{4}\right)n^2 - \frac{\delta}{8}n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} \ge \left(\frac{2}{3}+\frac{\delta}{8}\right)n. \end{align*} $$
$$ \begin{align*} |U_1|+|U_2| & \ge \frac{|L_{1,2}| - \frac{\delta}{16}n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} + \frac{2|L_{2}| - \frac{\delta}{16}n^2}{\left(\frac{2}{3}+\zeta^{1/2}\right)n} \\ & \ge \frac{|L_{1,2}| - \frac{\delta}{16}n^2 + |L_{2}| - \frac{\delta}{16}n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} \\ & = \frac{|L| - \frac{\delta}{8}n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} \ge \frac{\left(\frac{2}{9}+\frac{\delta}{4}\right)n^2 - \frac{\delta}{8}n^2}{\left(\frac{1}{3}+\zeta^{1/2}\right)n} \ge \left(\frac{2}{3}+\frac{\delta}{8}\right)n. \end{align*} $$
So it follows from (5.1) that
![]() $|U_1 \cap U_2| \ge |U_1|+|U_2| - |V_2| \ge \frac {\delta }{16}n$
.
$|U_1 \cap U_2| \ge |U_1|+|U_2| - |V_2| \ge \frac {\delta }{16}n$
.
Fix a vertex
![]() $w\in U_1 \cap U_2$
and a vertex
$w\in U_1 \cap U_2$
and a vertex
![]() $u\in N_{L}(w) \cap V_1$
. Let
$u\in N_{L}(w) \cap V_1$
. Let
![]() $V_2' = N_{L}(w) \cap V_2$
. Since
$V_2' = N_{L}(w) \cap V_2$
. Since
![]() $|V_2'| \ge \frac {\delta }{16}n$
, similar to (5.2), there exists an edge
$|V_2'| \ge \frac {\delta }{16}n$
, similar to (5.2), there exists an edge
![]() $ab\in L_{\mathcal {H}}(u) \cap \binom {V_2'}{2}$
. However, this implies that
$ab\in L_{\mathcal {H}}(u) \cap \binom {V_2'}{2}$
. However, this implies that
![]() $\mathbb {F}_{3,2} \subset \mathcal {H}[\{v,u,w,a,b\}]$
(see Figure 9), a contradiction. This completes the proof of Theorem 5.1.
$\mathbb {F}_{3,2} \subset \mathcal {H}[\{v,u,w,a,b\}]$
(see Figure 9), a contradiction. This completes the proof of Theorem 5.1.

Figure 9: Finding
![]() $\mathbb {F}_{3,2}$
when
$\mathbb {F}_{3,2}$
when
![]() $L_1 = \emptyset $
.
$L_1 = \emptyset $
.
6 Concluding remarks
By a small modification of the proof, one can easily extend Theorems 1.5 and 1.6 to vertex-disjoint union of different hypergraphs as follows (here, we omit the statement for the rainbow version).
Theorem 6.1 Let
![]() $m \ge r \ge 2, k \ge 1$
be integers and let
$m \ge r \ge 2, k \ge 1$
be integers and let
![]() $F_1, \ldots , F_{k}$
be nondegenerate r-graphs on at most m vertices. Suppose that there exists a constant
$F_1, \ldots , F_{k}$
be nondegenerate r-graphs on at most m vertices. Suppose that there exists a constant
![]() $c> 0$
such that for all
$c> 0$
such that for all
![]() $i\in [k]$
and large
$i\in [k]$
and large
![]() $n \colon $
$n \colon $
-
(a)
 $F_i$
is
$F_i$
is
 $\left (c\binom {n}{r-1}, \frac {1-\pi (F)}{4m}\binom {n}{r-1}\right )$
-bounded, and
$\left (c\binom {n}{r-1}, \frac {1-\pi (F)}{4m}\binom {n}{r-1}\right )$
-bounded, and -
(b)
 $\mathrm {ex}(n, F_i)$
is
$\mathrm {ex}(n, F_i)$
is
 $\frac {1-\pi (F)}{8m}\binom {n}{r-1}$
-smooth.
$\frac {1-\pi (F)}{8m}\binom {n}{r-1}$
-smooth.
Then there exist constant
![]() $N_0$
such that for all integers
$N_0$
such that for all integers
![]() $n \ge N_0$
and
$n \ge N_0$
and
![]() $t_1, \ldots , t_k \in \mathbb {N}$
with
$t_1, \ldots , t_k \in \mathbb {N}$
with
![]() $t+1:= \sum _{i=1}^{k}t_i \in [0, \varepsilon n]$
, where
$t+1:= \sum _{i=1}^{k}t_i \in [0, \varepsilon n]$
, where
![]() $\varepsilon = \min \left \{\frac {c}{4erm}, \frac {1-\pi (F_1)}{64rm^2}, \ldots , \frac {1-\pi (F_k)}{64rm^2}\right \}$
, we have
$\varepsilon = \min \left \{\frac {c}{4erm}, \frac {1-\pi (F_1)}{64rm^2}, \ldots , \frac {1-\pi (F_k)}{64rm^2}\right \}$
, we have
 $$ \begin{align*} \mathrm{ex}\left(n, \bigsqcup_{i=1}^{k}t_iF_i\right) \le \binom{n}{r}-\binom{n-t}{r} + \max_{i\in [k]}\left\{\mathrm{ex}(n-t, F_i)\right\}. \end{align*} $$
$$ \begin{align*} \mathrm{ex}\left(n, \bigsqcup_{i=1}^{k}t_iF_i\right) \le \binom{n}{r}-\binom{n-t}{r} + \max_{i\in [k]}\left\{\mathrm{ex}(n-t, F_i)\right\}. \end{align*} $$
Moreover, if
![]() $\max _{i\in [k]} \mathrm {ex}(n-t, F_i) = \mathrm {ex}(n, \{F_1, \ldots , F_k\})$
, then the inequality above can be replace by equality.
$\max _{i\in [k]} \mathrm {ex}(n-t, F_i) = \mathrm {ex}(n, \{F_1, \ldots , F_k\})$
, then the inequality above can be replace by equality.
Recall from Theorem 1.7 that for every r-uniform Turán pair
![]() $(F, P)$
, the function
$(F, P)$
, the function
![]() $\mathrm {ex}(n,F)$
is smooth. This result can be extended in the following ways with a slight modification to the proof (the proof of Theorem 6.2 below is included in the Appendix).
$\mathrm {ex}(n,F)$
is smooth. This result can be extended in the following ways with a slight modification to the proof (the proof of Theorem 6.2 below is included in the Appendix).
Let
![]() $(n_i)_{i=1}^{\infty }$
be an ascending sequence of integers, F be an r-graph, and P be a pattern. We say
$(n_i)_{i=1}^{\infty }$
be an ascending sequence of integers, F be an r-graph, and P be a pattern. We say
![]() $(F,P)$
is a
$(F,P)$
is a
![]() $(n_i)_{i=1}^{\infty }$
-Turán pair if there exists
$(n_i)_{i=1}^{\infty }$
-Turán pair if there exists
![]() $N_0$
such that
$N_0$
such that
-
• every P-construction is F-free, and
-
• for every
 $n_i \ge N_0$
, there exists an
$n_i \ge N_0$
, there exists an
 $n_i$
-vertex F-free extremal construction that is a P-construction.
$n_i$
-vertex F-free extremal construction that is a P-construction.
Let
![]() $k \ge 1$
be an integer. We say an ascending sequence of integers
$k \ge 1$
be an integer. We say an ascending sequence of integers
![]() $(n_i)_{i=1}^{\infty }$
is
$(n_i)_{i=1}^{\infty }$
is
![]() $\frac {1}{k}$
-dense if for every integer
$\frac {1}{k}$
-dense if for every integer
![]() $m \ge N_0$
, we have
$m \ge N_0$
, we have
Theorem 6.2 Let
![]() $k \ge 1$
be an integer, F be an r-graph, and P be a pattern. Suppose that
$k \ge 1$
be an integer, F be an r-graph, and P be a pattern. Suppose that
![]() $(F,P)$
is an
$(F,P)$
is an
![]() $(n_i)_{i=1}^{\infty }$
-Turán pair for some
$(n_i)_{i=1}^{\infty }$
-Turán pair for some
![]() $\frac {1}{k}$
-dense ascending sequence of integers
$\frac {1}{k}$
-dense ascending sequence of integers
![]() $(n_i)_{i=1}^{\infty }$
. Then
$(n_i)_{i=1}^{\infty }$
. Then
![]() $\mathrm {ex}(n, F)$
is
$\mathrm {ex}(n, F)$
is
![]() $16 k^2 \binom {n-1}{r-2}$
-smooth.
$16 k^2 \binom {n-1}{r-2}$
-smooth.
Given an r-graph F, we say F is
![]() $2$
-covered if every pair of vertices in
$2$
-covered if every pair of vertices in
![]() $V(F)$
is contained in some edge of F. In particular, complete r-graphs are
$V(F)$
is contained in some edge of F. In particular, complete r-graphs are
![]() $2$
-covered.
$2$
-covered.
Suppose that F is a
![]() $2$
-covered r-graph. Then it is easy to see that duplicating a vertex in an F-free r-graph does not change its F-freeness. Thus, a proof analogous to that of Fact 4.2 can show that
$2$
-covered r-graph. Then it is easy to see that duplicating a vertex in an F-free r-graph does not change its F-freeness. Thus, a proof analogous to that of Fact 4.2 can show that
![]() $\delta (n,F) \ge \Delta (\mathcal {H})$
for every maximum F-free r-graph
$\delta (n,F) \ge \Delta (\mathcal {H})$
for every maximum F-free r-graph
![]() $\mathcal {H}$
on
$\mathcal {H}$
on
![]() $n-1$
vertices. Consequently, we have
$n-1$
vertices. Consequently, we have
![]() $\delta (n,F) \ge d(n-1,F)$
. By combining this result with Fact 4.1 and Lemma 3.5, we can extend Theorem 6.3 as follows.
$\delta (n,F) \ge d(n-1,F)$
. By combining this result with Fact 4.1 and Lemma 3.5, we can extend Theorem 6.3 as follows.
Theorem 6.3 Suppose that F is a
![]() $2$
-covered r-graph. Then
$2$
-covered r-graph. Then
![]() $\mathrm {ex}(n, F)$
is
$\mathrm {ex}(n, F)$
is
![]() $4\binom {n-1}{r-2}$
-smooth.
$4\binom {n-1}{r-2}$
-smooth.
Recall that Allen, Böttcher, Hladký, and Piguet [Reference Allen, Böttcher, Hladký and Piguet2] determined, for large n, the value of
![]() $\mathrm {ex}(n, (t+1)K_3)$
for all
$\mathrm {ex}(n, (t+1)K_3)$
for all
![]() $t\le n/3$
. Considering that the situation is already very complicated for
$t\le n/3$
. Considering that the situation is already very complicated for
![]() $K_3$
, the following question seems very hard in general.
$K_3$
, the following question seems very hard in general.
Problem 6.4 Let
![]() $r \ge 2$
be an integer and F be a nondegenerate r-graph with m vertices. For large n determine
$r \ge 2$
be an integer and F be a nondegenerate r-graph with m vertices. For large n determine
![]() $\mathrm {ex}(n, (t+1)F)$
for all
$\mathrm {ex}(n, (t+1)F)$
for all
![]() $t \le n/m$
.
$t \le n/m$
.
A first step toward a full understanding of Problem 6.4 would be determining the regime of t in which members in ![]() are extremal. Here, we propose the following question, which seems feasible for many hypergraphs (including graphs).
are extremal. Here, we propose the following question, which seems feasible for many hypergraphs (including graphs).
Problem 6.5 Let
![]() $r \ge 2$
be an integer and F be an r-graph with m vertices. For large n determine the maximum value of
$r \ge 2$
be an integer and F be an r-graph with m vertices. For large n determine the maximum value of
![]() $s(n, F)$
such that
$s(n, F)$
such that
holds for all
![]() $t \in [0, s(n,F)]$
.
$t \in [0, s(n,F)]$
.
Understanding the asymptotic behavior of
![]() $s(n, F)$
would be also very interesting.
$s(n, F)$
would be also very interesting.
Problem 6.6 Let
![]() $r \ge 2$
be an integer and F be an r-graph with m vertices. Let
$r \ge 2$
be an integer and F be an r-graph with m vertices. Let
![]() $s(n, F)$
be the same as in Problem 6.5. Determine the value of
$s(n, F)$
be the same as in Problem 6.5. Determine the value of
![]() $\liminf _{n\to \infty } \frac {s(n,F)}{n}$
.
$\liminf _{n\to \infty } \frac {s(n,F)}{n}$
.
Note that the result of Allen, Böttcher, Hladký, and Piguet [Reference Allen, Böttcher, Hladký and Piguet2] implies that
![]() $s(n, K_3) = \frac {2n-6}{9}$
for large n. In particular,
$s(n, K_3) = \frac {2n-6}{9}$
for large n. In particular,
![]() $\lim _{n\to \infty } \frac {s(n,K_3)}{n} = \frac {2}{9}$
.
$\lim _{n\to \infty } \frac {s(n,K_3)}{n} = \frac {2}{9}$
.
It would be also interesting to consider extensions of the density Corrádi–Hajnal theorem to degenerate hypergraphs such as complete r-partite r-graphs and even cyclesFootnote 6 . The behavior for degenerate hypergraphs seems very different from nondegenerate hypergraphs, and we refer the reader to, for example, [Reference Fang, Zhai and Lin19, Theorem 1.3] for related results on even cycles.
As pointed out to us by Mubayi,
![]() $\mathrm {ex}(n,(t+1)F)$
is also related to the well-known Erdős–Rademacher Problem [Reference Erdős12]. More specifically, a lower bound for the number of copies of F in an n-vertex r-graph
$\mathrm {ex}(n,(t+1)F)$
is also related to the well-known Erdős–Rademacher Problem [Reference Erdős12]. More specifically, a lower bound for the number of copies of F in an n-vertex r-graph
![]() $\mathcal {H}$
with e edges can provide a lower bound for the number of vertex-disjoint copies of F in
$\mathcal {H}$
with e edges can provide a lower bound for the number of vertex-disjoint copies of F in
![]() $\mathcal {H}$
, as revealed by results in Hypergraph Matching Theory. However, this approach is unlikely to give a tight bound for
$\mathcal {H}$
, as revealed by results in Hypergraph Matching Theory. However, this approach is unlikely to give a tight bound for
![]() $\mathrm {ex}(n,(t+1)F)$
since these two questions generally have different extremal constructions. We refer the reader to, for example, [Reference Mubayi61, Reference Mubayi62, Reference Nikiforov64, Reference Razborov70–Reference Reiher72] and references therein for more results related to the Erdős–Rademacher Problem.
$\mathrm {ex}(n,(t+1)F)$
since these two questions generally have different extremal constructions. We refer the reader to, for example, [Reference Mubayi61, Reference Mubayi62, Reference Nikiforov64, Reference Razborov70–Reference Reiher72] and references therein for more results related to the Erdős–Rademacher Problem.
A Proof of Fact 4.3
Proof of Fact 4.3
Fix a sufficiently small
![]() $\varepsilon> 0$
and let n be a sufficiently large integer such that
$\varepsilon> 0$
and let n be a sufficiently large integer such that
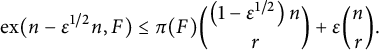 $$ \begin{align*} \mathrm{ex}(n-\varepsilon^{1/2}n, F) \le \pi(F) \binom{\left(1-\varepsilon^{1/2}\right) n}{r} +\varepsilon \binom{n}{r}. \end{align*} $$
$$ \begin{align*} \mathrm{ex}(n-\varepsilon^{1/2}n, F) \le \pi(F) \binom{\left(1-\varepsilon^{1/2}\right) n}{r} +\varepsilon \binom{n}{r}. \end{align*} $$
Suppose to the contrary that
![]() $|Z_{\varepsilon }(\mathcal {H})| \ge \varepsilon ^{1/2} n$
. Then fix a set
$|Z_{\varepsilon }(\mathcal {H})| \ge \varepsilon ^{1/2} n$
. Then fix a set
![]() $Z\subset Z_{\varepsilon }(\mathcal {H})$
of size
$Z\subset Z_{\varepsilon }(\mathcal {H})$
of size
![]() $\varepsilon ^{1/2} n$
and let
$\varepsilon ^{1/2} n$
and let ![]() . It follows from the definition of
. It follows from the definition of
![]() $Z_{\varepsilon }(\mathcal {H})$
that
$Z_{\varepsilon }(\mathcal {H})$
that
 $$ \begin{align*} |\mathcal{H}[U]| & \ge |\mathcal{H}| - |Z| \cdot \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n-1}{r-1} \\ & \ge \left(\pi(F) - \varepsilon\right)\binom{n}{r} - \frac{r}{n} \cdot |Z| \cdot \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n}{r} \\ & = \left(\pi(F) - \varepsilon\right)\binom{n}{r} - r\varepsilon^{1/2} \cdot \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n}{r} \\ & = \left((1-r \varepsilon^{1/2}) \pi(F) +(r^2-1)\varepsilon\right) \binom{n}{r}. \end{align*} $$
$$ \begin{align*} |\mathcal{H}[U]| & \ge |\mathcal{H}| - |Z| \cdot \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n-1}{r-1} \\ & \ge \left(\pi(F) - \varepsilon\right)\binom{n}{r} - \frac{r}{n} \cdot |Z| \cdot \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n}{r} \\ & = \left(\pi(F) - \varepsilon\right)\binom{n}{r} - r\varepsilon^{1/2} \cdot \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n}{r} \\ & = \left((1-r \varepsilon^{1/2}) \pi(F) +(r^2-1)\varepsilon\right) \binom{n}{r}. \end{align*} $$
On the other hand, we have
 $$ \begin{align*} |\mathcal{H}[U]| \le \mathrm{ex}(n-\varepsilon^{1/2}n, F) & \le \pi(F) \binom{\left(1-\varepsilon^{1/2}\right) n}{r} +\varepsilon \binom{n}{r} \\ & \le \left(1-\varepsilon^{1/2}\right)^{r} \pi(F) \binom{n}{r} +\varepsilon \binom{n}{r} \\ & \le \left(1-r \varepsilon^{1/2} + \binom{r}{2} \varepsilon\right) \pi(F) \binom{n}{r} +\varepsilon \binom{n}{r} \\ & \le \left(\left(1-r \varepsilon^{1/2}\right) \pi(F) + \left(\binom{r}{2}+1\right)\varepsilon \right) \binom{n}{r}. \end{align*} $$
$$ \begin{align*} |\mathcal{H}[U]| \le \mathrm{ex}(n-\varepsilon^{1/2}n, F) & \le \pi(F) \binom{\left(1-\varepsilon^{1/2}\right) n}{r} +\varepsilon \binom{n}{r} \\ & \le \left(1-\varepsilon^{1/2}\right)^{r} \pi(F) \binom{n}{r} +\varepsilon \binom{n}{r} \\ & \le \left(1-r \varepsilon^{1/2} + \binom{r}{2} \varepsilon\right) \pi(F) \binom{n}{r} +\varepsilon \binom{n}{r} \\ & \le \left(\left(1-r \varepsilon^{1/2}\right) \pi(F) + \left(\binom{r}{2}+1\right)\varepsilon \right) \binom{n}{r}. \end{align*} $$
Here, we used the inequality that
![]() $\left (1-x\right )^{r} \le 1-r x + \binom {r}{2} x^2$
for
$\left (1-x\right )^{r} \le 1-r x + \binom {r}{2} x^2$
for
![]() $x\in [0,1]$
and
$x\in [0,1]$
and
![]() $r\ge 2$
.
$r\ge 2$
.
Since
![]() $r^2-1> \binom {r}{2}+1$
for
$r^2-1> \binom {r}{2}+1$
for
![]() $r\ge 2$
, we arrived at a contradiction. Therefore, we have
$r\ge 2$
, we arrived at a contradiction. Therefore, we have
![]() $|Z_{\varepsilon }(\mathcal {H})| \le \varepsilon ^{1/2} n$
. It follows that the induced subgraph
$|Z_{\varepsilon }(\mathcal {H})| \le \varepsilon ^{1/2} n$
. It follows that the induced subgraph
![]() $\mathcal {H}^{\prime }$
of
$\mathcal {H}^{\prime }$
of
![]() $\mathcal {H}$
on
$\mathcal {H}$
on
![]() $V(\mathcal {H})-Z_{\varepsilon }(\mathcal {H})$
satisfies
$V(\mathcal {H})-Z_{\varepsilon }(\mathcal {H})$
satisfies
 $$ \begin{align*} \delta(\mathcal{H}^{\prime}) & \ge \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n-1}{r-1} - |Z_{\varepsilon}(\mathcal{H})| \binom{n-2}{r-2} \\ & \ge \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n-1}{r-1} - \varepsilon^{1/2}n\cdot \frac{r-1}{n-1} \binom{n-1}{r-1} \\ & \ge \left(\pi(F)-2r \varepsilon^{1/2}\right)\binom{n-1}{r-1}, \end{align*} $$
$$ \begin{align*} \delta(\mathcal{H}^{\prime}) & \ge \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n-1}{r-1} - |Z_{\varepsilon}(\mathcal{H})| \binom{n-2}{r-2} \\ & \ge \left(\pi(F)-r \varepsilon^{1/2}\right)\binom{n-1}{r-1} - \varepsilon^{1/2}n\cdot \frac{r-1}{n-1} \binom{n-1}{r-1} \\ & \ge \left(\pi(F)-2r \varepsilon^{1/2}\right)\binom{n-1}{r-1}, \end{align*} $$
completing the proof of Fact 4.3.
B Proof of Theorem 6.2
The following fact can be derived from a slight modification of the proof of Fact 4.2
![]() $\colon $
instead of duplicating the vertex v just once, we duplicate it
$\colon $
instead of duplicating the vertex v just once, we duplicate it
![]() $n-n_{i_{\ast }}$
times.
$n-n_{i_{\ast }}$
times.
Fact B.1 Let
![]() $k \ge 1$
be an integer and
$k \ge 1$
be an integer and
![]() $(n_i)_{i=1}^{\infty }$
be a
$(n_i)_{i=1}^{\infty }$
be a
![]() $\frac {1}{k}$
-dense ascending sequence of integers. Suppose that
$\frac {1}{k}$
-dense ascending sequence of integers. Suppose that
![]() $(F,P)$
is an r-uniform
$(F,P)$
is an r-uniform
![]() $(n_i)_{i=1}^{\infty }$
-Turán pair and
$(n_i)_{i=1}^{\infty }$
-Turán pair and
![]() $\mathcal {H}$
is a maximum P-construction on
$\mathcal {H}$
is a maximum P-construction on
![]() $n_{i_{\ast }}$
vertices, where
$n_{i_{\ast }}$
vertices, where
![]() $i_{\ast }$
is sufficiently large. Then for every
$i_{\ast }$
is sufficiently large. Then for every
![]() $n \ge n_{i_{\ast }}$
, we have
$n \ge n_{i_{\ast }}$
, we have
Proof of Theorem 6.2
Let n be a sufficiently large integer and let
![]() $i_{\ast }$
be such that
$i_{\ast }$
be such that
![]() $n_{i_{\ast }} \le n \le n_{i_{\ast }} +k$
. The existence of such an
$n_{i_{\ast }} \le n \le n_{i_{\ast }} +k$
. The existence of such an
![]() $i_{\ast }$
is guaranteed by the assumption that
$i_{\ast }$
is guaranteed by the assumption that
![]() $(n_i)_{i=1}^{\infty }$
is a
$(n_i)_{i=1}^{\infty }$
is a
![]() $\frac {1}{k}$
-dense ascending sequence.
$\frac {1}{k}$
-dense ascending sequence.
Let ![]() . Notice that
. Notice that
 $$ \begin{align*} \Phi & \overset{\text{Fact}~\text{B.1}} = \mathrm{ex}(n,F)-\mathrm{ex}(n_{i_{\ast}},F) - (n-n_{i_{\ast}}) \cdot d(n_{i_{\ast}}, F) \\&\hspace{10pt} = \sum_{j=1}^{n-n_{i_{\ast}}} \left(\mathrm{ex}(n_{i_{\ast}}+j,F)-\mathrm{ex}(n_{i_{\ast}}+j-1,F) - d(n_{i_{\ast}}, F)\right) \\& \overset{\text{Fact}~4.1}\le \sum_{j=1}^{n-n_{i_{\ast}}} \left(d(n_{i_{\ast}}+j, F) - d(n_{i_{\ast}}, F) \right) \\&\hspace{-6pt}\overset{\text{Lemma~}3.5}\le \sum_{j=1}^{n-n_{i_{\ast}}} 4 j \binom{n_{i_{\ast}}}{r-2} \le 4\left(n-n_{i_{\ast}}\right)^2 \binom{n_{i_{\ast}}}{r-2}. \end{align*} $$
$$ \begin{align*} \Phi & \overset{\text{Fact}~\text{B.1}} = \mathrm{ex}(n,F)-\mathrm{ex}(n_{i_{\ast}},F) - (n-n_{i_{\ast}}) \cdot d(n_{i_{\ast}}, F) \\&\hspace{10pt} = \sum_{j=1}^{n-n_{i_{\ast}}} \left(\mathrm{ex}(n_{i_{\ast}}+j,F)-\mathrm{ex}(n_{i_{\ast}}+j-1,F) - d(n_{i_{\ast}}, F)\right) \\& \overset{\text{Fact}~4.1}\le \sum_{j=1}^{n-n_{i_{\ast}}} \left(d(n_{i_{\ast}}+j, F) - d(n_{i_{\ast}}, F) \right) \\&\hspace{-6pt}\overset{\text{Lemma~}3.5}\le \sum_{j=1}^{n-n_{i_{\ast}}} 4 j \binom{n_{i_{\ast}}}{r-2} \le 4\left(n-n_{i_{\ast}}\right)^2 \binom{n_{i_{\ast}}}{r-2}. \end{align*} $$
Additionally,
 $$ \begin{align*} & d(n,F) - \delta(n,F) \\ &\hspace{-10.5pt} \overset{\text{Fact}~4.1} \le \left(d(n,F) - \delta(n,F)\right) + \sum_{j=1}^{n-n_{i_{\ast}}-1} \left(d(n-j,F) - \delta(n-j,F)\right) \\ & = \sum_{j=0}^{n-n_{i_{\ast}}-1} d(n-j,F) - \sum_{j=0}^{n-n_{i_{\ast}}-1} \delta(n-j,F) \\ & = \sum_{j=0}^{n-n_{i_{\ast}}-1} \left(d(n-j,F) -d(n_{i_{\ast}},F)\right) + (n-n_{i_{\ast}}) \cdot d(n_{i_{\ast}},F) - \left(\mathrm{ex}(n,F) - \mathrm{ex}(n_{i_{\ast}},F)\right) \\ & \le \sum_{j=0}^{n-n_{i_{\ast}}-1} \left|d(n-j,F) -d(n_{i_{\ast}},F)\right| + \Phi \\ &\hspace{-14pt}\overset{\text{Lemma~}3.5} \le 4(n-n_{i_{\ast}})^2 \binom{n_{i_{\ast}}}{r-2} + 4(n-n_{i_{\ast}})^2 \binom{n_{i_{\ast}}}{r-2} = 8 (n-n_{i_{\ast}})^2 \binom{n_{i_{\ast}}}{r-2}. \end{align*} $$
$$ \begin{align*} & d(n,F) - \delta(n,F) \\ &\hspace{-10.5pt} \overset{\text{Fact}~4.1} \le \left(d(n,F) - \delta(n,F)\right) + \sum_{j=1}^{n-n_{i_{\ast}}-1} \left(d(n-j,F) - \delta(n-j,F)\right) \\ & = \sum_{j=0}^{n-n_{i_{\ast}}-1} d(n-j,F) - \sum_{j=0}^{n-n_{i_{\ast}}-1} \delta(n-j,F) \\ & = \sum_{j=0}^{n-n_{i_{\ast}}-1} \left(d(n-j,F) -d(n_{i_{\ast}},F)\right) + (n-n_{i_{\ast}}) \cdot d(n_{i_{\ast}},F) - \left(\mathrm{ex}(n,F) - \mathrm{ex}(n_{i_{\ast}},F)\right) \\ & \le \sum_{j=0}^{n-n_{i_{\ast}}-1} \left|d(n-j,F) -d(n_{i_{\ast}},F)\right| + \Phi \\ &\hspace{-14pt}\overset{\text{Lemma~}3.5} \le 4(n-n_{i_{\ast}})^2 \binom{n_{i_{\ast}}}{r-2} + 4(n-n_{i_{\ast}})^2 \binom{n_{i_{\ast}}}{r-2} = 8 (n-n_{i_{\ast}})^2 \binom{n_{i_{\ast}}}{r-2}. \end{align*} $$
Therefore, we obtain that
 $$ \begin{align*} \left|\delta(n,F) - d(n-1,F)\right| & = \left| \delta(n,F) - d(n,F) + d(n,F) - d(n-1,F) \right| \\ &\hspace{-14pt}\overset{\text{Lemma~}3.5} \le \left| \delta(n,F) - d(n,F) \right| + 4\binom{n-1}{r-2} \\ &\le 8 (n-n_{i_{\ast}})^2 \binom{n_{i_{\ast}}}{r-2} + 4\binom{n-1}{r-2} \le 12 k^2 \binom{n-1}{r-2}, \end{align*} $$
$$ \begin{align*} \left|\delta(n,F) - d(n-1,F)\right| & = \left| \delta(n,F) - d(n,F) + d(n,F) - d(n-1,F) \right| \\ &\hspace{-14pt}\overset{\text{Lemma~}3.5} \le \left| \delta(n,F) - d(n,F) \right| + 4\binom{n-1}{r-2} \\ &\le 8 (n-n_{i_{\ast}})^2 \binom{n_{i_{\ast}}}{r-2} + 4\binom{n-1}{r-2} \le 12 k^2 \binom{n-1}{r-2}, \end{align*} $$
proving Theorem 6.2.
Acknowledgements
We would like to express our gratitude to both referees for their valuable suggestions and comments.