Search

Skip to main content Accessibility help

Home
Search

Only show content I have access to (0)

Articles (1)

Over 3 years (1)

From year:

To year:

Apply

Mathematics (1)

tubular neighborhood.

ESAIM: Probability and Statistics (1)

View selected items
Save to my bookmarks
Export citations
Download PDF (zip)
Save to Kindle
Save to Dropbox
Save to Google Drive
Save content to
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .

To save content items to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Please be advised that item(s) you selected are not available.
You are about to save
Your Kindle email address

Please provide your Kindle email.

@free.kindle.com @kindle.com (service fees apply)

By using this service, you agree that you will only keep content for personal use, and will not openly distribute them via Dropbox, Google Drive or other file sharing services

1 results

A graph-based estimator of the number of clusters
Gérard Biau, Benoît Cadre, Bruno Pelletier
Journal:

ESAIM: Probability and Statistics / Volume 11 / June 2007

Published online by Cambridge University Press:

19 June 2007, pp. 272-280

Print publication:

June 2007
- Article
- - Get access
    
    Check if you have access via personal or institutional login
    
    Log in Register
- Export citation
Assessing the number of clusters of a statistical population is one of the essential issues of unsupervised learning. Given n independent observations X1,...,Xn drawn from an unknown multivariate probability density f, we propose a new approach to estimate the number of connected components, or clusters, of the t-level set $\mathcal L(t)=\{x:f(x) \geq t\}$ 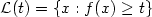. The basic idea is to form a rough skeleton of the set $\mathcal L(t)$ using any preliminary estimator of f, and to count the number of connected components of the resulting graph. Under mild analytic conditions on f, and using tools from differential geometry, we establish the consistency of our method.