Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Maier, Markus
Hein, Matthias
and
von Luxburg, Ulrike
2009.
Optimal construction of k-nearest-neighbor graphs for identifying noisy clusters.
Theoretical Computer Science,
Vol. 410,
Issue. 19,
p.
1749.
Carlsson, Gunnar
and
Mémoli, Facundo
2010.
Classification as a Tool for Research.
p.
63.
Rinaldo, Alessandro
and
Wasserman, Larry
2010.
Generalized density clustering.
The Annals of Statistics,
Vol. 38,
Issue. 5,
Koepke, Hoyt A.
and
Clarke, Bertrand S.
2011.
On the limits of clustering in high dimensions via cost functions.
Statistical Analysis and Data Mining: The ASA Data Science Journal,
Vol. 4,
Issue. 1,
p.
30.
Arias-Castro, Ery
2011.
Clustering Based on Pairwise Distances When the Data is of Mixed Dimensions.
IEEE Transactions on Information Theory,
Vol. 57,
Issue. 3,
p.
1692.
Arias-Castro, Ery
Pelletier, Bruno
and
Pudlo, Pierre
2012.
The Normalized Graph Cut and Cheeger Constant: From Discrete to Continuous.
Advances in Applied Probability,
Vol. 44,
Issue. 4,
p.
907.
Arias-Castro, Ery
Pelletier, Bruno
and
Pudlo, Pierre
2012.
The Normalized Graph Cut and Cheeger Constant: From Discrete to Continuous.
Advances in Applied Probability,
Vol. 44,
Issue. 4,
p.
907.
Laloë, T.
and
Servien, R.
2013.
Nonparametric estimation of regression level sets using kernel plug-in estimator.
Journal of the Korean Statistical Society,
Vol. 42,
Issue. 3,
p.
301.
Auray, Stéphane
Klutchnikoff, Nicolas
and
Rouvière, Laurent
2015.
On clustering procedures and nonparametric mixture estimation.
Electronic Journal of Statistics,
Vol. 9,
Issue. 1,
Arias-Castro, Ery
and
Rodríguez-Casal, Alberto
2017.
On estimating the perimeter using the alpha-shape.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 53,
Issue. 3,
Holmström, Lasse
Karttunen, Kyösti
and
Klemelä, Jussi
2017.
Estimation of level set trees using adaptive partitions.
Computational Statistics,
Vol. 32,
Issue. 3,
p.
1139.
Binder, Patricia
Muma, Michael
and
Zoubir, Abdelhak M.
2018.
Gravitational Clustering: A simple, robust and adaptive approach for distributed networks.
Signal Processing,
Vol. 149,
Issue. ,
p.
36.
Klemelä, Jussi
2018.
Level set tree methods.
WIREs Computational Statistics,
Vol. 10,
Issue. 5,
Kumar, Dheeraj
Ghafoori, Zahra
Bezdek, James C.
Leckie, Christopher
Ramamohanarao, Kotagiri
and
Palaniswami, Marimuthu
2018.
Dealing with Inliers in Feature Vector Data.
International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems,
Vol. 26,
Issue. Suppl. 2,
p.
25.
Qiao, Wanli
and
Polonik, Wolfgang
2019.
Nonparametric confidence regions for level sets: Statistical properties and geometry.
Electronic Journal of Statistics,
Vol. 13,
Issue. 1,
Qiao, Wanli
2020.
Asymptotics and optimal bandwidth for nonparametric estimation of density level sets.
Electronic Journal of Statistics,
Vol. 14,
Issue. 1,
Klutchnikoff, Nicolas
Poterie, Audrey
and
Rouvière, Laurent
2022.
Statistical analysis of a hierarchical clustering algorithm with outliers.
Journal of Multivariate Analysis,
Vol. 192,
Issue. ,
p.
105075.
Saavedra-Nieves, Paula
and
Crujeiras, Rosa M.
2022.
Nonparametric estimation of directional highest density regions.
Advances in Data Analysis and Classification,
Vol. 16,
Issue. 3,
p.
761.
Saavedra-Nieves, Paula
and
Fernández-Pérez, Martín
2024.
Directional density-based clustering.
Advances in Data Analysis and Classification,
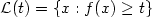 . The basic idea is to form a rough skeleton of the set $\mathcal L(t)$
. The basic idea is to form a rough skeleton of the set $\mathcal L(t)$  using any preliminary estimator of f, and to count the number of connected components of the resulting graph. Under mild analytic conditions on f, and using tools from differential geometry, we establish the consistency of our method.
using any preliminary estimator of f, and to count the number of connected components of the resulting graph. Under mild analytic conditions on f, and using tools from differential geometry, we establish the consistency of our method.