We consider a family of discrete Jacobi operators on the one-dimensional integer latticewith Laplacian and potential terms modulated by a primitive invertible two-lettersubstitution. We investigate the spectrum and the spectral type, the fractal structure andfractal dimensions of the spectrum, exact dimensionality of the integrated density ofstates, and the gap structure. We present a review of previous results, some applications,and open problems. Our investigation is based largely on the dynamics of trace maps. Thiswork is an extension of similar results on Schrödinger operators, although some of theresults that we obtain differ qualitatively and quantitatively from those for theSchrödinger operators. The nontrivialities of this extension lie in the dynamics of theassociated trace map as one attempts to extend the trace map formalism from theSchrödinger cocycle to the Jacobi one. In fact, the Jacobi operators considered here are,in a sense, a test item, as many other models can be attacked via the same techniques, andwe present an extensive discussion on this.

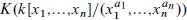 . This naturally leads to a new generalization of the big Witt vectors. If
. This naturally leads to a new generalization of the big Witt vectors. If 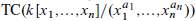 as the iterated homotopy cofiber of an
as the iterated homotopy cofiber of an 