We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A result of Haglund implies that the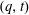 
$(q,t)$-bigraded Hilbert series of the space of diagonal harmonics is a 
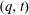$(q,t)$-Ehrhart function of the flow polytope of a complete graph with netflow vector 
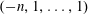$(-n,1,\ldots ,1)$. We study the 
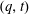$(q,t)$-Ehrhart functions of flow polytopes of threshold graphs with arbitrary netflow vectors. Our results generalize previously known specializations of the mentioned bigraded Hilbert series at 
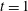$t=1$, 
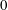$0$, and 
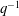$q^{-1}$. As a corollary to our results, we obtain a proof of a conjecture of Armstrong, Garsia, Haglund, Rhoades, and Sagan about the 
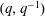$(q,q^{-1})$-Ehrhart function of the flow polytope of a complete graph with an arbitrary netflow vector.
