We continue our study of strongly unbounded colorings, this time focusing on subadditive maps. In Part I of this series, we showed that, for many pairs of infinite cardinals 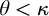 $\theta < \kappa $, the existence of a strongly unbounded coloring
$\theta < \kappa $, the existence of a strongly unbounded coloring 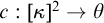 $c:[\kappa ]^2 \rightarrow \theta $ is a theorem of
$c:[\kappa ]^2 \rightarrow \theta $ is a theorem of 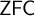 $\textsf{ZFC}$. Adding the requirement of subadditivity to a strongly unbounded coloring is a significant strengthening, though, and here we see that in many cases the existence of a subadditive strongly unbounded coloring
$\textsf{ZFC}$. Adding the requirement of subadditivity to a strongly unbounded coloring is a significant strengthening, though, and here we see that in many cases the existence of a subadditive strongly unbounded coloring 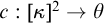 $c:[\kappa ]^2 \rightarrow \theta $ is independent of
$c:[\kappa ]^2 \rightarrow \theta $ is independent of 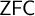 $\textsf{ZFC}$. We connect the existence of subadditive strongly unbounded colorings with a number of other infinitary combinatorial principles, including the narrow system property, the existence of
$\textsf{ZFC}$. We connect the existence of subadditive strongly unbounded colorings with a number of other infinitary combinatorial principles, including the narrow system property, the existence of 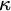 $\kappa $-Aronszajn trees with ascent paths, and square principles. In particular, we show that the existence of a closed, subadditive, strongly unbounded coloring
$\kappa $-Aronszajn trees with ascent paths, and square principles. In particular, we show that the existence of a closed, subadditive, strongly unbounded coloring 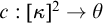 $c:[\kappa ]^2 \rightarrow \theta $ is equivalent to a certain weak indexed square principle
$c:[\kappa ]^2 \rightarrow \theta $ is equivalent to a certain weak indexed square principle 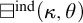 $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$. We conclude the paper with an application to the failure of the infinite productivity of
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$. We conclude the paper with an application to the failure of the infinite productivity of 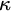 $\kappa $-stationarily layered posets, answering a question of Cox.
$\kappa $-stationarily layered posets, answering a question of Cox.