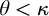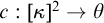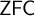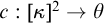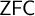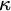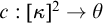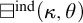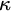1 Introduction
For any pair
![]() $\theta < \kappa $
of infinite regular cardinals, the positive partition relation
$\theta < \kappa $
of infinite regular cardinals, the positive partition relation
![]() $\kappa \rightarrow (\kappa )^2_{\theta }$
, which asserts that every coloring
$\kappa \rightarrow (\kappa )^2_{\theta }$
, which asserts that every coloring
![]() $c:[\kappa ]^2 \rightarrow \theta $
has a homogeneous set of cardinality
$c:[\kappa ]^2 \rightarrow \theta $
has a homogeneous set of cardinality
![]() $\kappa $
, is equivalent to
$\kappa $
, is equivalent to
![]() $\kappa $
being weakly compact. For non-weakly compact cardinals
$\kappa $
being weakly compact. For non-weakly compact cardinals
![]() $\kappa $
, though, one can seek to measure the incompactness of
$\kappa $
, though, one can seek to measure the incompactness of
![]() $\kappa $
by asking whether certain strengthenings of the negative relation
$\kappa $
by asking whether certain strengthenings of the negative relation
![]() $\kappa \nrightarrow (\kappa )^2_{\theta }$
hold. One natural such strengthening is to require that there exist colorings
$\kappa \nrightarrow (\kappa )^2_{\theta }$
hold. One natural such strengthening is to require that there exist colorings
![]() $c:[\kappa ]^2 \rightarrow \theta $
witnessing certain strong unboundedness properties. In [Reference Lambie-Hanson and Rinot20], which forms Part I of this series of papers, the authors introduce the following coloring principle, which asserts the existence of such strongly unbounded colorings, and use it to answer questions about the infinite productivity of the
$c:[\kappa ]^2 \rightarrow \theta $
witnessing certain strong unboundedness properties. In [Reference Lambie-Hanson and Rinot20], which forms Part I of this series of papers, the authors introduce the following coloring principle, which asserts the existence of such strongly unbounded colorings, and use it to answer questions about the infinite productivity of the
![]() $\kappa $
-Knaster condition for uncountable
$\kappa $
-Knaster condition for uncountable
![]() $\kappa $
.
$\kappa $
.
Definition 1.1.
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
asserts the existence of a coloring
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
asserts the existence of a coloring
![]() $c:[\kappa ]^2 \rightarrow \theta $
such that for every
$c:[\kappa ]^2 \rightarrow \theta $
such that for every
![]() $\sigma < \chi $
, every pairwise disjoint subfamily
$\sigma < \chi $
, every pairwise disjoint subfamily
![]() $\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
$\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
![]() $\kappa $
, and every
$\kappa $
, and every
![]() $i < \theta $
, there exists
$i < \theta $
, there exists
![]() $\mathcal {B} \in [\mathcal {A}]^{\mu }$
such that
$\mathcal {B} \in [\mathcal {A}]^{\mu }$
such that
![]() $\min (c[a \times b])> i$
for all
$\min (c[a \times b])> i$
for all
![]() $a, b \in \mathcal {B}$
with
$a, b \in \mathcal {B}$
with
![]() $\sup (a)<\min (b)$
.
$\sup (a)<\min (b)$
.
Much of [Reference Lambie-Hanson and Rinot20] is devoted to analyzing situations in which
![]() $\operatorname {\mathrm {U}}(\ldots )$
necessarily holds and, moreover, is witnessed by closed or somewhere-closed colorings (see Definition 2.1). In Part II of this series [Reference Lambie-Hanson and Rinot22], we studied
$\operatorname {\mathrm {U}}(\ldots )$
necessarily holds and, moreover, is witnessed by closed or somewhere-closed colorings (see Definition 2.1). In Part II of this series [Reference Lambie-Hanson and Rinot22], we studied
![]() $\operatorname {\mathrm {Cspec}}(\kappa )$
, the C-sequence spectrum of
$\operatorname {\mathrm {Cspec}}(\kappa )$
, the C-sequence spectrum of
![]() $\kappa $
(see Definition 5.5), which is another measure of the incompactness of
$\kappa $
(see Definition 5.5), which is another measure of the incompactness of
![]() $\kappa $
, and found some unexpected connections between
$\kappa $
, and found some unexpected connections between
![]() $\operatorname {\mathrm {Cspec}}(\kappa )$
and the validity of instances of
$\operatorname {\mathrm {Cspec}}(\kappa )$
and the validity of instances of
![]() $\operatorname {\mathrm {U}}(\kappa ,\ldots )$
.
$\operatorname {\mathrm {U}}(\kappa ,\ldots )$
.
In this paper, which can be read largely independently of [Reference Lambie-Hanson and Rinot20, Reference Lambie-Hanson and Rinot22], we investigate subadditive witnesses to
![]() $\operatorname {\mathrm {U}}(\ldots )$
.
$\operatorname {\mathrm {U}}(\ldots )$
.
Definition 1.2. A coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
is subadditive if, for all
$c:[\kappa ]^2\rightarrow \theta $
is subadditive if, for all
![]() $\alpha < \beta < \gamma < \kappa $
, the following inequalities hold:
$\alpha < \beta < \gamma < \kappa $
, the following inequalities hold:
-
(1)
 $c(\alpha , \gamma ) \leq \max \{c(\alpha , \beta ), c(\beta , \gamma )\}$
;
$c(\alpha , \gamma ) \leq \max \{c(\alpha , \beta ), c(\beta , \gamma )\}$
; -
(2)
 $c(\alpha , \beta ) \leq \max \{c(\alpha , \gamma ), c(\beta , \gamma )\}$
.
$c(\alpha , \beta ) \leq \max \{c(\alpha , \gamma ), c(\beta , \gamma )\}$
.
Adding the requirement of subadditivity significantly strengthens the coloring principle, and we prove that the existence of closed, subadditive witnesses to
![]() $\operatorname {\mathrm {U}}(\ldots )$
is equivalent to a certain indexed square principle. Our first main result improves Clause (1) of [Reference Lambie-Hanson and Rinot20, Theorem A].Footnote
1
$\operatorname {\mathrm {U}}(\ldots )$
is equivalent to a certain indexed square principle. Our first main result improves Clause (1) of [Reference Lambie-Hanson and Rinot20, Theorem A].Footnote
1
Theorem A. Let
![]() $\theta <\kappa $
be a pair of infinite regular cardinals. The following are equivalent:
$\theta <\kappa $
be a pair of infinite regular cardinals. The following are equivalent:
-
(1)
 $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds.
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds. -
(2) There is a closed, subadditive witness to
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. -
(3) There is a closed, subadditive witness to
 $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\sup (\operatorname {\mathrm {Reg}}(\kappa ))$
.
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\sup (\operatorname {\mathrm {Reg}}(\kappa ))$
.
In addition,
![]() $\square (\kappa , \sqsubseteq _{\theta })$
implies
$\square (\kappa , \sqsubseteq _{\theta })$
implies
![]() $(1)$
–
$(1)$
–
![]() $(3)$
.
$(3)$
.
We also prove that a version of square with built-in diamond for a singular cardinal
![]() $\lambda $
gives rise to somewhere-closed subadditive witnesses to
$\lambda $
gives rise to somewhere-closed subadditive witnesses to
![]() $\operatorname {\mathrm {U}}(\lambda ^+, \ldots )$
, which in turn imply that the C-sequence spectrum of
$\operatorname {\mathrm {U}}(\lambda ^+, \ldots )$
, which in turn imply that the C-sequence spectrum of
![]() $\lambda ^+$
is rich:
$\lambda ^+$
is rich:
Theorem B. Suppose that
![]() $\lambda $
is a singular cardinal,
$\lambda $
is a singular cardinal,
![]() $\vec f$
is a scale for
$\vec f$
is a scale for
![]() $\lambda $
of length
$\lambda $
of length
![]() $\lambda ^+$
in some product
$\lambda ^+$
in some product
![]() $\prod \vec \lambda $
, and
$\prod \vec \lambda $
, and
![]() holds. Let
holds. Let
![]() $\Sigma $
denote the set of good points for
$\Sigma $
denote the set of good points for
![]() $\vec f$
.
$\vec f$
.
Then, for every
![]() $\theta \in \operatorname {\mathrm {Reg}}(\lambda )\setminus (\operatorname {\mathrm {cf}}(\lambda )+1)$
, there exists a
$\theta \in \operatorname {\mathrm {Reg}}(\lambda )\setminus (\operatorname {\mathrm {cf}}(\lambda )+1)$
, there exists a
![]() $\Sigma $
-closed, subadditive witness to
$\Sigma $
-closed, subadditive witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
. In particular,
$\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
. In particular,
![]() $\operatorname {\mathrm {Reg}}(\lambda )\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
$\operatorname {\mathrm {Reg}}(\lambda )\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
For a pair of infinite regular cardinals
![]() $\theta <\kappa $
and a coloring
$\theta <\kappa $
and a coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
, an interesting facet of the study of the unboundedness properties of c is the set
$c:[\kappa ]^2\rightarrow \theta $
, an interesting facet of the study of the unboundedness properties of c is the set
![]() $\partial (c)$
of its levels of divergence (see Definition 3.21). Any coloring c for which
$\partial (c)$
of its levels of divergence (see Definition 3.21). Any coloring c for which
![]() $\partial (c)$
is stationary is automatically a somewhere-closed witness to
$\partial (c)$
is stationary is automatically a somewhere-closed witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\theta )$
. We prove that the existence of a (fully) closed witness c to
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\theta )$
. We prove that the existence of a (fully) closed witness c to
![]() $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\theta )$
for which
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\theta )$
for which
![]() $\partial (c)$
is stationary is equivalent to the existence of a nonreflecting stationary subset of
$\partial (c)$
is stationary is equivalent to the existence of a nonreflecting stationary subset of
![]() $E^{\kappa }_{\theta }$
, and that the existence of a nonreflecting stationary subset of
$E^{\kappa }_{\theta }$
, and that the existence of a nonreflecting stationary subset of
![]() $E^{\kappa }_{\theta }$
does not suffice to yield a subadditive witness to
$E^{\kappa }_{\theta }$
does not suffice to yield a subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. We have three main consistency results concerning the characteristic
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. We have three main consistency results concerning the characteristic
![]() $\partial (c)$
:
$\partial (c)$
:
Theorem C.
-
(1) For any pair of infinite regular cardinals
 $\theta <\kappa $
, there is a
$\theta <\kappa $
, there is a
 $\kappa $
-strategically closed,
$\kappa $
-strategically closed,
 $\theta ^+$
-directed closed forcing notion that adds a subadditive witness c to
$\theta ^+$
-directed closed forcing notion that adds a subadditive witness c to
 $\operatorname {\mathrm {U}}(\kappa , \kappa ,\theta , \theta )$
for which
$\operatorname {\mathrm {U}}(\kappa , \kappa ,\theta , \theta )$
for which
 $\partial (c)$
is stationary.
$\partial (c)$
is stationary. -
(2) For any pair of infinite regular cardinals
 $\theta <\kappa $
, there is a
$\theta <\kappa $
, there is a
 $\kappa $
-strategically closed,
$\kappa $
-strategically closed,
 $\theta $
-directed closed forcing notion that adds a closed subadditive witness c to
$\theta $
-directed closed forcing notion that adds a closed subadditive witness c to
 $\operatorname {\mathrm {U}}(\kappa , \kappa ,\theta , \theta )$
for which
$\operatorname {\mathrm {U}}(\kappa , \kappa ,\theta , \theta )$
for which
 $\partial (c)$
is stationary.
$\partial (c)$
is stationary. -
(3) For regular uncountable cardinals
 $\theta <\lambda <\kappa $
such that
$\theta <\lambda <\kappa $
such that
 $\lambda $
is supercompact and
$\lambda $
is supercompact and
 $\kappa $
is weakly compact, there is a forcing extension in which
$\kappa $
is weakly compact, there is a forcing extension in which
 $\square (\kappa ,\theta )$
fails
$\square (\kappa ,\theta )$
fails
 $;$
yet, there is a closed, subadditive witness c to
$;$
yet, there is a closed, subadditive witness c to
 $\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \theta )$
for which
$\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \theta )$
for which
 $\partial (c)$
is stationary.
$\partial (c)$
is stationary.
On the Ramsey-theoretic side, we prove that in the presence of large cardinals, for many pairs of infinite regular cardinals
![]() $\theta <\kappa $
, there are no subadditive witnesses to
$\theta <\kappa $
, there are no subadditive witnesses to
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, i.e.,
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, i.e.,
![]() $\kappa \rightarrow [\kappa ]^2_{\theta ,<\theta }$
holds restricted to the class of subadditive colorings. We also show that similar results hold at small cardinals in forcing extensions or in the presence of forcing axioms.
$\kappa \rightarrow [\kappa ]^2_{\theta ,<\theta }$
holds restricted to the class of subadditive colorings. We also show that similar results hold at small cardinals in forcing extensions or in the presence of forcing axioms.
On the anti-Ramsey-theoretic side, we have a result reminiscent of the motivating result of [Reference Lambie-Hanson and Rinot20] concerning the infinite productivity of strong forms of the
![]() $\kappa $
-chain condition. When combined with Theorem A, the next theorem shows that
$\kappa $
-chain condition. When combined with Theorem A, the next theorem shows that
![]() $\square (\kappa )$
yields a gallery of counterexamples to productivity of
$\square (\kappa )$
yields a gallery of counterexamples to productivity of
![]() $\kappa $
-stationarily layered posets, answering a question of Cox [Reference Cox and Lücke5].
$\kappa $
-stationarily layered posets, answering a question of Cox [Reference Cox and Lücke5].
Theorem D. Suppose that
![]() $\theta \leq \chi < \kappa $
are infinite, regular cardinals,
$\theta \leq \chi < \kappa $
are infinite, regular cardinals,
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\chi $
-inaccessible, and there is a closed and subadditive witness c to
${<}\chi $
-inaccessible, and there is a closed and subadditive witness c to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. Then there is a sequence of posets
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. Then there is a sequence of posets
![]() $\langle \mathbb {P}_i \mathrel {|} i < \theta \rangle $
such that:
$\langle \mathbb {P}_i \mathrel {|} i < \theta \rangle $
such that:
-
(1) for all
 $i < \theta $
,
$i < \theta $
,
 $\mathbb {P}_i$
is well-met and
$\mathbb {P}_i$
is well-met and
 $\chi $
-directed closed with greatest lower bounds;
$\chi $
-directed closed with greatest lower bounds; -
(2) for all
 $j < \theta $
,
$j < \theta $
,
 $\prod _{i < j} \mathbb {P}_i$
is
$\prod _{i < j} \mathbb {P}_i$
is
 $\kappa $
-stationarily layered;
$\kappa $
-stationarily layered; -
(3)
 $\prod _{i < \theta } \mathbb {P}_i$
is not
$\prod _{i < \theta } \mathbb {P}_i$
is not
 $\kappa $
-cc.
$\kappa $
-cc.
If, in addition,
![]() $\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then the sequence
$\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then the sequence
![]() $\langle \mathbb P_i\mathrel {|} i<\theta \rangle $
can be made constant.
$\langle \mathbb P_i\mathrel {|} i<\theta \rangle $
can be made constant.
As a corollary, we get that Magidor’s forcing for changing the cofinality of a measurable cardinal
![]() $\lambda $
to a regular cardinal
$\lambda $
to a regular cardinal
![]() $\theta <\lambda $
adds a poset
$\theta <\lambda $
adds a poset
![]() $\mathbb P$
whose
$\mathbb P$
whose
![]() $\theta ^{\text {th}}$
power is not
$\theta ^{\text {th}}$
power is not
![]() $\lambda ^+$
-cc, but all of whose lower powers are
$\lambda ^+$
-cc, but all of whose lower powers are
![]() $\lambda ^+$
-stationarily layered.
$\lambda ^+$
-stationarily layered.
1.1 Organization of this paper
In Section 2, we present some useful definitions and facts about
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
, largely derived from Part I of this series. We also present a pseudo-inverse to the fact, observed in Part I, that Shelah’s principle
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
, largely derived from Part I of this series. We also present a pseudo-inverse to the fact, observed in Part I, that Shelah’s principle
![]() $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
implies
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
implies
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
.
In Section 3, we review the notion of subadditivity and some of its variations and prove that any subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
is in fact a witness to
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
is in fact a witness to
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
for all
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
for all
![]() $\mu < \kappa $
and all
$\mu < \kappa $
and all
![]() $\chi \leq \operatorname {\mathrm {cf}}(\theta )$
(and, under certain closure assumptions, even stronger principles). Section 3.1 contains results connecting subadditive strongly unbounded colorings to narrow systems and trees with ascent paths. In Section 3.2, we discuss locally small colorings of the form
$\chi \leq \operatorname {\mathrm {cf}}(\theta )$
(and, under certain closure assumptions, even stronger principles). Section 3.1 contains results connecting subadditive strongly unbounded colorings to narrow systems and trees with ascent paths. In Section 3.2, we discuss locally small colorings of the form
![]() $c:[\lambda ^+]^2 \rightarrow \operatorname {\mathrm {cf}}(\lambda )$
, focusing in particular on the case in which
$c:[\lambda ^+]^2 \rightarrow \operatorname {\mathrm {cf}}(\lambda )$
, focusing in particular on the case in which
![]() $\lambda $
is a singular cardinal. Locally small colorings are necessarily witnesses to
$\lambda $
is a singular cardinal. Locally small colorings are necessarily witnesses to
![]() $\operatorname {\mathrm {U}}(\lambda ^+, 2, \operatorname {\mathrm {cf}}(\lambda ), \operatorname {\mathrm {cf}}(\lambda ))$
, and retain this property in any outer model with the same cardinals. In Section 3.3, we introduce a subset
$\operatorname {\mathrm {U}}(\lambda ^+, 2, \operatorname {\mathrm {cf}}(\lambda ), \operatorname {\mathrm {cf}}(\lambda ))$
, and retain this property in any outer model with the same cardinals. In Section 3.3, we introduce a subset
![]() $\partial (c) \subseteq \kappa $
associated with a coloring
$\partial (c) \subseteq \kappa $
associated with a coloring
![]() $c:[\kappa ]^2 \rightarrow \theta $
that is useful in the analysis of
$c:[\kappa ]^2 \rightarrow \theta $
that is useful in the analysis of
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
, particularly in the context of subadditive colorings. We then introduce a forcing notion that establishes Clause (1) of Theorem C. Section 3.4 contains a number of results indicating the extent to which various compactness principles place limits on the existence of certain subadditive witnesses to
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
, particularly in the context of subadditive colorings. We then introduce a forcing notion that establishes Clause (1) of Theorem C. Section 3.4 contains a number of results indicating the extent to which various compactness principles place limits on the existence of certain subadditive witnesses to
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
. In particular, it is shown that simultaneous stationary reflection, the existence of highly complete or indecomposable ultrafilters, and the P-ideal dichotomy all have such an effect.
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
. In particular, it is shown that simultaneous stationary reflection, the existence of highly complete or indecomposable ultrafilters, and the P-ideal dichotomy all have such an effect.
In Section 4, we introduce an indexed square principle
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
and prove that it is equivalent to the existence of a closed, subadditive witness to
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
and prove that it is equivalent to the existence of a closed, subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, thereby establishing the first part of Theorem A. We also prove a consistency result indicating that
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, thereby establishing the first part of Theorem A. We also prove a consistency result indicating that
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
is a proper weakening of
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
is a proper weakening of
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
and does not even imply
$\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
and does not even imply
![]() $\square (\kappa , \theta )$
, in the process proving Clause (3) of Theorem C. Section 4 also contains the proof of the second part of Theorem A and the proof of Clause (2) of Theorem C.
$\square (\kappa , \theta )$
, in the process proving Clause (3) of Theorem C. Section 4 also contains the proof of the second part of Theorem A and the proof of Clause (2) of Theorem C.
Section 5 is concerned with successors of singular cardinals. We begin by proving Theorem B, showing that a certain square with built-in diamond sequence on a singular cardinal
![]() $\lambda $
entails the existence of a subadditive witness to
$\lambda $
entails the existence of a subadditive witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
for all
$\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
for all
![]() $\theta \in \operatorname {\mathrm {Reg}}(\lambda )\setminus (\operatorname {\mathrm {cf}}(\lambda )+1)$
. We then present an improvement upon a result from Part I of this series proving the existence of closed witnesses to
$\theta \in \operatorname {\mathrm {Reg}}(\lambda )\setminus (\operatorname {\mathrm {cf}}(\lambda )+1)$
. We then present an improvement upon a result from Part I of this series proving the existence of closed witnesses to
![]() $\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \operatorname {\mathrm {cf}}(\lambda ))$
for all singular
$\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \operatorname {\mathrm {cf}}(\lambda ))$
for all singular
![]() $\lambda $
whose cofinality is not greatly Mahlo and all
$\lambda $
whose cofinality is not greatly Mahlo and all
![]() $\theta \leq \operatorname {\mathrm {cf}}(\lambda )$
.
$\theta \leq \operatorname {\mathrm {cf}}(\lambda )$
.
Section 6 deals with the infinity productivity of
![]() $\kappa $
-stationarily layered posets and contains our proof of Theorem D.
$\kappa $
-stationarily layered posets and contains our proof of Theorem D.
1.2 Notation and conventions
Throughout the paper,
![]() $\kappa $
denotes a regular uncountable cardinal, and
$\kappa $
denotes a regular uncountable cardinal, and
![]() $\chi ,\theta ,$
and
$\chi ,\theta ,$
and
![]() $\mu $
denote cardinals
$\mu $
denote cardinals
![]() $\le \kappa $
.
$\le \kappa $
.
![]() $\lambda $
will always denote an infinite cardinal. We say that
$\lambda $
will always denote an infinite cardinal. We say that
![]() $\kappa $
is
$\kappa $
is
![]() $\chi $
-inaccessible iff, for all
$\chi $
-inaccessible iff, for all
![]() $\nu <\kappa $
,
$\nu <\kappa $
,
![]() $\nu ^{\chi }<\kappa $
, and say that
$\nu ^{\chi }<\kappa $
, and say that
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\chi $
-inaccessible iff, for all
${<}\chi $
-inaccessible iff, for all
![]() $\nu <\kappa $
and
$\nu <\kappa $
and
![]() $\mu <\chi $
,
$\mu <\chi $
,
![]() $\nu ^{\mu }<\kappa $
. For a regular cardinal
$\nu ^{\mu }<\kappa $
. For a regular cardinal
![]() $\Upsilon $
, we denote by
$\Upsilon $
, we denote by
![]() $H_{\Upsilon }$
the collection of all sets of hereditary cardinality less than
$H_{\Upsilon }$
the collection of all sets of hereditary cardinality less than
![]() $\Upsilon $
.
$\Upsilon $
.
![]() $\operatorname {\mathrm {Reg}}$
denotes the class of infinite regular cardinals, and
$\operatorname {\mathrm {Reg}}$
denotes the class of infinite regular cardinals, and
![]() $\operatorname {\mathrm {Reg}}(\kappa )$
denotes
$\operatorname {\mathrm {Reg}}(\kappa )$
denotes
![]() $\operatorname {\mathrm {Reg}} \cap \kappa $
.
$\operatorname {\mathrm {Reg}} \cap \kappa $
.
![]() $E^{\kappa }_{\chi }$
denotes the set
$E^{\kappa }_{\chi }$
denotes the set
![]() $\{\alpha < \kappa \mathrel {|} \operatorname {\mathrm {cf}}(\alpha ) = \chi \}$
, and
$\{\alpha < \kappa \mathrel {|} \operatorname {\mathrm {cf}}(\alpha ) = \chi \}$
, and
![]() $E^{\kappa }_{\geq \chi }$
,
$E^{\kappa }_{\geq \chi }$
,
![]() $E^{\kappa }_{<\chi }$
,
$E^{\kappa }_{<\chi }$
,
![]() $E^{\kappa }_{\neq \chi }$
, etc. are defined analogously.
$E^{\kappa }_{\neq \chi }$
, etc. are defined analogously.
For a set of ordinals a, we write
![]() $\operatorname {\mathrm {ssup}}(a) := \sup \{\alpha + 1 \mathrel {|} \alpha \in a\}$
,
$\operatorname {\mathrm {ssup}}(a) := \sup \{\alpha + 1 \mathrel {|} \alpha \in a\}$
,
![]() $\operatorname {\mathrm {acc}}^+(a) := \{\alpha < \operatorname {\mathrm {ssup}}(a) \mathrel {|} \sup (a \cap \alpha ) = \alpha> 0\}$
,
$\operatorname {\mathrm {acc}}^+(a) := \{\alpha < \operatorname {\mathrm {ssup}}(a) \mathrel {|} \sup (a \cap \alpha ) = \alpha> 0\}$
,
![]() $\operatorname {\mathrm {acc}}(a) := a \cap \operatorname {\mathrm {acc}}^+(a)$
,
$\operatorname {\mathrm {acc}}(a) := a \cap \operatorname {\mathrm {acc}}^+(a)$
,
![]() $\operatorname {\mathrm {nacc}}(a) := a \setminus \operatorname {\mathrm {acc}}(a)$
, and
$\operatorname {\mathrm {nacc}}(a) := a \setminus \operatorname {\mathrm {acc}}(a)$
, and
![]() $\operatorname {\mathrm {cl}}(a):= a\cup \operatorname {\mathrm {acc}}^+(a)$
. For sets of ordinals a and b, we write
$\operatorname {\mathrm {cl}}(a):= a\cup \operatorname {\mathrm {acc}}^+(a)$
. For sets of ordinals a and b, we write
![]() $a < b$
if, for all
$a < b$
if, for all
![]() $\alpha \in a$
and all
$\alpha \in a$
and all
![]() $\beta \in b$
, we have
$\beta \in b$
, we have
![]() $\alpha < \beta $
. For a set of ordinals a and an ordinal
$\alpha < \beta $
. For a set of ordinals a and an ordinal
![]() $\beta $
, we write
$\beta $
, we write
![]() $a < \beta $
instead of
$a < \beta $
instead of
![]() $a < \{\beta \}$
and
$a < \{\beta \}$
and
![]() $\beta < a$
instead of
$\beta < a$
instead of
![]() $\{\beta \} < a$
.
$\{\beta \} < a$
.
For any set
![]() $\mathcal A$
, we write
$\mathcal A$
, we write
![]() $[\mathcal A]^{\chi }:=\{ \mathcal B\subseteq \mathcal A\mathrel {|} |\mathcal B|=\chi \}$
and
$[\mathcal A]^{\chi }:=\{ \mathcal B\subseteq \mathcal A\mathrel {|} |\mathcal B|=\chi \}$
and
![]() $[\mathcal A]^{<\chi }:=\{\mathcal B\subseteq \mathcal A\mathrel {|} |\mathcal B|<\chi \}$
. In particular,
$[\mathcal A]^{<\chi }:=\{\mathcal B\subseteq \mathcal A\mathrel {|} |\mathcal B|<\chi \}$
. In particular,
![]() $[\mathcal {A}]^2$
consists of all unordered pairs from
$[\mathcal {A}]^2$
consists of all unordered pairs from
![]() $\mathcal {A}$
. In some scenarios, we will also be interested in ordered pairs from
$\mathcal {A}$
. In some scenarios, we will also be interested in ordered pairs from
![]() $\mathcal {A}$
. In particular, if
$\mathcal {A}$
. In particular, if
![]() $\mathcal {A}$
is either a set of ordinals or a collection of sets of ordinals, then we will abuse notation and write
$\mathcal {A}$
is either a set of ordinals or a collection of sets of ordinals, then we will abuse notation and write
![]() $(a,b) \in [\mathcal {A}]^2$
to mean
$(a,b) \in [\mathcal {A}]^2$
to mean
![]() $\{a,b\} \in [\mathcal {A}]^2$
and
$\{a,b\} \in [\mathcal {A}]^2$
and
![]() $a < b$
.
$a < b$
.
2 Preliminaries
In this brief section, we recall a key definition and present a few useful facts about
![]() $\operatorname {\mathrm {U}}(\ldots )$
. We start by recalling the following definition from [Reference Lambie-Hanson and Rinot20] concerning closed colorings.
$\operatorname {\mathrm {U}}(\ldots )$
. We start by recalling the following definition from [Reference Lambie-Hanson and Rinot20] concerning closed colorings.
Definition 2.1. Suppose that
![]() $c:[\kappa ]^2 \rightarrow \theta $
is a coloring.
$c:[\kappa ]^2 \rightarrow \theta $
is a coloring.
-
(1) For all
 $\beta < \kappa $
and
$\beta < \kappa $
and
 $i \leq \theta $
, we let
$i \leq \theta $
, we let
 $D^c_{\leq i}(\beta )$
denote the set
$D^c_{\leq i}(\beta )$
denote the set
 $\{\alpha < \beta \mathrel {|} c(\alpha , \beta ) \leq i\}$
.
$\{\alpha < \beta \mathrel {|} c(\alpha , \beta ) \leq i\}$
. -
(2) For all
 $\Sigma \subseteq \kappa $
, c is
$\Sigma \subseteq \kappa $
, c is
 $\Sigma $
-closed if, for all
$\Sigma $
-closed if, for all
 $\beta < \kappa $
and
$\beta < \kappa $
and
 $i \leq \theta $
,
$i \leq \theta $
,  $$\begin{align*}\operatorname{\mathrm{acc}}^+(D^c_{\leq i}(\beta)) \cap \Sigma \subseteq D^c_{\leq i}(\beta). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{acc}}^+(D^c_{\leq i}(\beta)) \cap \Sigma \subseteq D^c_{\leq i}(\beta). \end{align*}$$
-
(3) c is somewhere-closed if it is
 $\Sigma $
-closed for some stationary
$\Sigma $
-closed for some stationary
 $\Sigma \subseteq \kappa $
.
$\Sigma \subseteq \kappa $
. -
(4) c is closed if it is
 $\kappa $
-closed.
$\kappa $
-closed.
The following fact is a useful tool for proving that certain colorings satisfy strong instances of
![]() $\operatorname {\mathrm {U}}(\ldots )$
.
$\operatorname {\mathrm {U}}(\ldots )$
.
Fact 2.2 [Reference Lambie-Hanson and Rinot20].
Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
is a coloring and
$c:[\kappa ]^2\rightarrow \theta $
is a coloring and
![]() $\omega \le \chi <\kappa $
. Then
$\omega \le \chi <\kappa $
. Then
![]() $(1)\implies (2)\implies (3)$
:
$(1)\implies (2)\implies (3)$
:
-
(1) For some stationary
 $\Sigma \subseteq E^{\kappa }_{\ge \chi }$
, c is a
$\Sigma \subseteq E^{\kappa }_{\ge \chi }$
, c is a
 $\Sigma $
-closed witness to
$\Sigma $
-closed witness to
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
. -
(2) For every family
 $\mathcal A\subseteq [\kappa ]^{<\chi }$
consisting of
$\mathcal A\subseteq [\kappa ]^{<\chi }$
consisting of
 $\kappa $
-many pairwise disjoint sets, for every club
$\kappa $
-many pairwise disjoint sets, for every club
 $D\subseteq \kappa $
, and for every
$D\subseteq \kappa $
, and for every
 $i<\theta $
, there exist
$i<\theta $
, there exist
 $\gamma \in D$
,
$\gamma \in D$
,
 $a\in \mathcal A$
, and
$a\in \mathcal A$
, and
 $\epsilon < \gamma $
such that:
$\epsilon < \gamma $
such that:-
•
 $\gamma < a$
;
$\gamma < a$
; -
• for all
 $\alpha \in (\epsilon , \gamma )$
and all
$\alpha \in (\epsilon , \gamma )$
and all
 $\beta \in a$
, we have
$\beta \in a$
, we have
 $c(\alpha ,\beta )>i$
.
$c(\alpha ,\beta )>i$
.
-
-
(3) c witnesses
 $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\chi )$
.
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\chi )$
.
It is sometimes useful to consider the following unbalanced form of
![]() $\operatorname {\mathrm {U}}(\cdots )$
.
$\operatorname {\mathrm {U}}(\cdots )$
.
Definition 2.3.
![]() $\operatorname {\mathrm {U}}(\kappa , \mu \circledast \nu , \theta , \chi )$
asserts the existence of a coloring
$\operatorname {\mathrm {U}}(\kappa , \mu \circledast \nu , \theta , \chi )$
asserts the existence of a coloring
![]() $c:[\kappa ]^2 \rightarrow \theta $
such that for every
$c:[\kappa ]^2 \rightarrow \theta $
such that for every
![]() $\sigma < \chi $
, every pairwise disjoint subfamily
$\sigma < \chi $
, every pairwise disjoint subfamily
![]() $\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
$\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
![]() $\kappa $
, and every
$\kappa $
, and every
![]() $i < \theta $
, there exist
$i < \theta $
, there exist
![]() $\mathcal A'\in [\mathcal A]^{\mu }$
and
$\mathcal A'\in [\mathcal A]^{\mu }$
and
![]() $\mathcal B'\in [\mathcal A]^{\nu }$
such that, for every
$\mathcal B'\in [\mathcal A]^{\nu }$
such that, for every
![]() $(a,b)\in \mathcal A'\times \mathcal B'$
,
$(a,b)\in \mathcal A'\times \mathcal B'$
,
![]() $a<b$
and
$a<b$
and
![]() $\min (c[a \times b])> i$
.
$\min (c[a \times b])> i$
.
Lemma 2.4. Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
witnesses
$c:[\kappa ]^2\rightarrow \theta $
witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, with
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, with
![]() $\theta <\kappa $
.
$\theta <\kappa $
.
-
(1) For every cofinal
 $A\subseteq \kappa $
, there exists
$A\subseteq \kappa $
, there exists
 $\epsilon <\kappa $
such that
$\epsilon <\kappa $
such that  $$ \begin{align*} \sup\{\beta\in A\setminus\epsilon\mathrel{|} \sup\{c(\alpha, \beta) \mathrel{|} \alpha \in A \cap \epsilon\}=\theta\}=\kappa. \end{align*} $$
$$ \begin{align*} \sup\{\beta\in A\setminus\epsilon\mathrel{|} \sup\{c(\alpha, \beta) \mathrel{|} \alpha \in A \cap \epsilon\}=\theta\}=\kappa. \end{align*} $$
-
(2) For every cofinal
 $A\subseteq \kappa $
, there exists
$A\subseteq \kappa $
, there exists
 $\beta \in A$
such that
$\beta \in A$
such that
 $\{c(\alpha , \beta ) \mathrel {|} \alpha \in A \cap \beta \}$
is unbounded in
$\{c(\alpha , \beta ) \mathrel {|} \alpha \in A \cap \beta \}$
is unbounded in
 $\theta $
. In particular, c witnesses
$\theta $
. In particular, c witnesses
 $\operatorname {\mathrm {U}}(\kappa ,\operatorname {\mathrm {cf}}(\theta )\circledast 1,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,\operatorname {\mathrm {cf}}(\theta )\circledast 1,\theta ,2)$
. -
(3) For every stationary
 $S\subseteq \kappa $
, there exists
$S\subseteq \kappa $
, there exists
 $\epsilon <\kappa $
such that, for every
$\epsilon <\kappa $
such that, for every
 $i<\theta $
,
$i<\theta $
,
 $\{\beta \in S\mathrel {|} \epsilon <\beta , ~ c(\epsilon ,\beta )>i\}$
is stationary.
$\{\beta \in S\mathrel {|} \epsilon <\beta , ~ c(\epsilon ,\beta )>i\}$
is stationary. -
(4) For every stationary
 $S\subseteq \kappa $
and a family of functions
$S\subseteq \kappa $
and a family of functions
 $\mathcal H\in [{}^S\theta ]^{<\kappa }$
, there exists
$\mathcal H\in [{}^S\theta ]^{<\kappa }$
, there exists
 $\epsilon \in S$
such that, for every
$\epsilon \in S$
such that, for every
 $h\in \mathcal H$
, the following set is stationary:
$h\in \mathcal H$
, the following set is stationary:  $$ \begin{align*} \{\beta\in S\mathrel{|} \epsilon<\beta, ~ c(\epsilon,\beta)>\max\{h(\epsilon),h(\beta)\}\}. \end{align*} $$
$$ \begin{align*} \{\beta\in S\mathrel{|} \epsilon<\beta, ~ c(\epsilon,\beta)>\max\{h(\epsilon),h(\beta)\}\}. \end{align*} $$
Proof Clause (2) follows from Clause (1), and Clause (3) follows from Clause (4).
(1) Towards a contradiction, suppose that A is a counterexample. Then, for every
![]() $\epsilon <\kappa $
, there exists a large enough
$\epsilon <\kappa $
, there exists a large enough
![]() $\eta _{\epsilon }\in [\epsilon ,\kappa )$
such that, for every
$\eta _{\epsilon }\in [\epsilon ,\kappa )$
such that, for every
![]() $\beta \in A\setminus \eta _{\epsilon }$
and for some
$\beta \in A\setminus \eta _{\epsilon }$
and for some
![]() $i < \theta $
,
$i < \theta $
,
![]() $A \cap \epsilon \subseteq D^c_{\leq i}(\beta )$
. Fix a sparse enough cofinal subset
$A \cap \epsilon \subseteq D^c_{\leq i}(\beta )$
. Fix a sparse enough cofinal subset
![]() $A'\subseteq A$
such that, for every
$A'\subseteq A$
such that, for every
![]() $\epsilon \in A'$
,
$\epsilon \in A'$
,
![]() $\min (A'\setminus (\epsilon +1))\ge \eta _{\epsilon +1}$
. It follows that, for every
$\min (A'\setminus (\epsilon +1))\ge \eta _{\epsilon +1}$
. It follows that, for every
![]() $\beta \in A'$
and for some
$\beta \in A'$
and for some
![]() $i_{\beta }<\theta $
,
$i_{\beta }<\theta $
,
![]() $A \cap \beta \subseteq D^c_{\leq i_{\beta }}(\beta )$
. Fix
$A \cap \beta \subseteq D^c_{\leq i_{\beta }}(\beta )$
. Fix
![]() $i^* < \theta $
and an unbounded
$i^* < \theta $
and an unbounded
![]() $A^* \subseteq A'$
such that
$A^* \subseteq A'$
such that
![]() $i_{\beta } = i^*$
for all
$i_{\beta } = i^*$
for all
![]() $\beta \in A^*$
. Since c witnesses
$\beta \in A^*$
. Since c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, we can find
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, we can find
![]() $(\alpha , \beta ) \in [A^*]^2$
such that
$(\alpha , \beta ) \in [A^*]^2$
such that
![]() $c(\alpha , \beta )> i^*$
, contradicting the fact that
$c(\alpha , \beta )> i^*$
, contradicting the fact that
![]() $\alpha \in A \cap \beta \subseteq D^c_{\leq i^*}(\beta )$
.
$\alpha \in A \cap \beta \subseteq D^c_{\leq i^*}(\beta )$
.
(4) Towards a contradiction, suppose that S and
![]() $\mathcal H$
form a counterexample. For every
$\mathcal H$
form a counterexample. For every
![]() $\epsilon \in S$
, fix a function
$\epsilon \in S$
, fix a function
![]() $h_{\epsilon }\in \mathcal H$
and a club
$h_{\epsilon }\in \mathcal H$
and a club
![]() $D_{\epsilon }\subseteq \kappa $
disjoint from
$D_{\epsilon }\subseteq \kappa $
disjoint from
![]() $\{\beta \in S\mathrel {|} \epsilon <\beta , ~ c(\epsilon ,\beta )>\max \{h_{\epsilon }(\epsilon ),h_{\epsilon }(\beta )\}\}$
. Let
$\{\beta \in S\mathrel {|} \epsilon <\beta , ~ c(\epsilon ,\beta )>\max \{h_{\epsilon }(\epsilon ),h_{\epsilon }(\beta )\}\}$
. Let
![]() $D:=\bigtriangleup _{\epsilon <\kappa }D_{\epsilon }$
. As
$D:=\bigtriangleup _{\epsilon <\kappa }D_{\epsilon }$
. As
![]() $|\mathcal H|<\kappa $
, find
$|\mathcal H|<\kappa $
, find
![]() $h\in \mathcal H$
for which
$h\in \mathcal H$
for which
![]() $A:=\{\epsilon \in D\cap S\mathrel {|} h_{\epsilon }=h\}$
is cofinal in
$A:=\{\epsilon \in D\cap S\mathrel {|} h_{\epsilon }=h\}$
is cofinal in
![]() $\kappa $
. As
$\kappa $
. As
![]() $\theta <\kappa $
, find
$\theta <\kappa $
, find
![]() $i<\theta $
for which
$i<\theta $
for which
![]() $B:=\{\beta \in A\mathrel {|} h(\beta )=i\}$
is cofinal in
$B:=\{\beta \in A\mathrel {|} h(\beta )=i\}$
is cofinal in
![]() $\kappa $
. Now, as c witnesses
$\kappa $
. Now, as c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, we may pick
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, we may pick
![]() $(\epsilon ,\beta )\in [B]^2$
such that
$(\epsilon ,\beta )\in [B]^2$
such that
![]() $c(\epsilon ,\beta )>i$
. But
$c(\epsilon ,\beta )>i$
. But
![]() $i=\max \{h_{\epsilon }(\epsilon ),h_{\epsilon }(\beta )\}$
, contradicting the fact that
$i=\max \{h_{\epsilon }(\epsilon ),h_{\epsilon }(\beta )\}$
, contradicting the fact that
![]() $\beta \in D_{\epsilon }\cap S$
.
$\beta \in D_{\epsilon }\cap S$
.
The following is a corollary to a result from [Reference Lambie-Hanson and Rinot20] which we never took the time to derive.
Proposition 2.5. If
![]() $\kappa $
is a Mahlo cardinal admitting a nonreflecting stationary subset of
$\kappa $
is a Mahlo cardinal admitting a nonreflecting stationary subset of
![]() $\operatorname {\mathrm {Reg}}(\kappa )$
, then
$\operatorname {\mathrm {Reg}}(\kappa )$
, then
![]() $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\kappa )$
holds for every
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\kappa )$
holds for every
![]() $\theta \leq \kappa $
.
$\theta \leq \kappa $
.
Proof By [Reference Lambie-Hanson and Rinot20, Theorem 4.11].
Recall that Shelah’s principle
![]() $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
asserts the existence of a coloring
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
asserts the existence of a coloring
![]() $c:[\kappa ]^2 \rightarrow \theta $
such that for every
$c:[\kappa ]^2 \rightarrow \theta $
such that for every
![]() $\sigma < \chi $
, every pairwise disjoint subfamily
$\sigma < \chi $
, every pairwise disjoint subfamily
![]() $\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
$\mathcal {A} \subseteq [\kappa ]^{\sigma }$
of size
![]() $\kappa $
, and every
$\kappa $
, and every
![]() $i < \theta $
, there exist
$i < \theta $
, there exist
![]() $(a,b)\in [\mathcal A]^2$
such that
$(a,b)\in [\mathcal A]^2$
such that
![]() $c[a \times b]=\{i\}$
. By [Reference Lambie-Hanson and Rinot20, Lemma 2.3],
$c[a \times b]=\{i\}$
. By [Reference Lambie-Hanson and Rinot20, Lemma 2.3],
![]() $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
implies
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
implies
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
. Here we deal with a pseudo-inverse:
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
. Here we deal with a pseudo-inverse:
Proposition 2.6. Suppose that
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
holds with
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
holds with
![]() $\chi \le \operatorname {\mathrm {cf}}(\theta )=\theta \le \theta ^{<\theta }<\kappa $
. Then
$\chi \le \operatorname {\mathrm {cf}}(\theta )=\theta \le \theta ^{<\theta }<\kappa $
. Then
![]() $V^{\operatorname {\mathrm {Add}}(\theta ,1)}\models \operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
.
$V^{\operatorname {\mathrm {Add}}(\theta ,1)}\models \operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
.
Proof In V, let
![]() $c:[\kappa ]^2\rightarrow \theta $
be a witness to
$c:[\kappa ]^2\rightarrow \theta $
be a witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
. Let G be
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,\chi )$
. Let G be
![]() $\operatorname {\mathrm {Add}}(\theta , 1)$
-generic over V, and work for now in
$\operatorname {\mathrm {Add}}(\theta , 1)$
-generic over V, and work for now in
![]() $V^{\operatorname {\mathrm {Add}}(\theta ,1)}$
. Let
$V^{\operatorname {\mathrm {Add}}(\theta ,1)}$
. Let
![]() $g:\theta \rightarrow \theta $
be the Cohen-generic function, and set
$g:\theta \rightarrow \theta $
be the Cohen-generic function, and set
![]() $d:=g\circ c$
. To see that d witnesses
$d:=g\circ c$
. To see that d witnesses
![]() $\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
, let
$\operatorname {\mathrm {Pr}}_1(\kappa ,\kappa ,\theta ,\chi )$
, let
![]() $\mathcal A$
be a
$\mathcal A$
be a
![]() $\kappa $
-sized pairwise disjoint subfamily of
$\kappa $
-sized pairwise disjoint subfamily of
![]() $[\kappa ]^{<\chi }$
, and let
$[\kappa ]^{<\chi }$
, and let
![]() $\tau <\theta $
; we need to find
$\tau <\theta $
; we need to find
![]() $(a,b)\in [\mathcal A]^2$
such that
$(a,b)\in [\mathcal A]^2$
such that
![]() $d[a\times b]=\{\tau \}$
. Since
$d[a\times b]=\{\tau \}$
. Since
![]() $\chi \leq \theta $
, every element of
$\chi \leq \theta $
, every element of
![]() $\mathcal {A}$
is in V. Also, letting
$\mathcal {A}$
is in V. Also, letting
![]() $\dot {\mathcal {A}} \in V$
be an
$\dot {\mathcal {A}} \in V$
be an
![]() $\operatorname {\mathrm {Add}}(\theta , 1)$
-name for
$\operatorname {\mathrm {Add}}(\theta , 1)$
-name for
![]() $\mathcal {A}$
, we can fix for each
$\mathcal {A}$
, we can fix for each
![]() $a \in \mathcal {A}$
a condition
$a \in \mathcal {A}$
a condition
![]() $p_a \in G$
such that
$p_a \in G$
such that
![]() $p_a \Vdash "a \in \dot {\mathcal {A}}."$
As
$p_a \Vdash "a \in \dot {\mathcal {A}}."$
As
![]() $\chi \le \theta ^{<\theta }<\kappa $
, and hence
$\chi \le \theta ^{<\theta }<\kappa $
, and hence
![]() $|\operatorname {\mathrm {Add}}(\theta , 1)| < \kappa $
, by passing to a subfamily if necessary, we may assume that there is a fixed
$|\operatorname {\mathrm {Add}}(\theta , 1)| < \kappa $
, by passing to a subfamily if necessary, we may assume that there is a fixed
![]() $p^* \in G$
such that
$p^* \in G$
such that
![]() $p_a = p^*$
for all
$p_a = p^*$
for all
![]() $a \in \mathcal {A}$
, and therefore
$a \in \mathcal {A}$
, and therefore
![]() $\mathcal A = \{a \in [\kappa ]^{<\chi } \mathrel {|} p \Vdash "a \in \dot {\mathcal {A}}"\}$
is in V. We therefore move back to V and run a density argument. Let
$\mathcal A = \{a \in [\kappa ]^{<\chi } \mathrel {|} p \Vdash "a \in \dot {\mathcal {A}}"\}$
is in V. We therefore move back to V and run a density argument. Let
![]() $p:i\rightarrow \theta $
be an arbitrary condition in
$p:i\rightarrow \theta $
be an arbitrary condition in
![]() $\operatorname {\mathrm {Add}}(\theta ,1)$
below
$\operatorname {\mathrm {Add}}(\theta ,1)$
below
![]() $p^*$
. By the hypothesis on c, pick
$p^*$
. By the hypothesis on c, pick
![]() $(a,b)\in [\mathcal A]^2$
such that
$(a,b)\in [\mathcal A]^2$
such that
![]() $x:=c[a\times b]$
is disjoint from i. Let
$x:=c[a\times b]$
is disjoint from i. Let
![]() $j:=\operatorname {\mathrm {ssup}}(x)$
, and let
$j:=\operatorname {\mathrm {ssup}}(x)$
, and let
![]() $q:j\rightarrow \theta $
be some condition extending p and satisfying
$q:j\rightarrow \theta $
be some condition extending p and satisfying
![]() $q(\xi )=\tau $
for all
$q(\xi )=\tau $
for all
![]() $\xi \in x$
. Clearly,
$\xi \in x$
. Clearly,
![]() $q(c(\alpha ,\beta ))=\tau $
for all
$q(c(\alpha ,\beta ))=\tau $
for all
![]() $(\alpha ,\beta )\in a\times b$
, so q forces that
$(\alpha ,\beta )\in a\times b$
, so q forces that
![]() $d[a\times b]=\{\tau \}$
, as sought.
$d[a\times b]=\{\tau \}$
, as sought.
We conclude this short section with another simple fact worth recording.
Proposition 2.7. If
![]() $\kappa $
is weakly compact, then, in
$\kappa $
is weakly compact, then, in
![]() $V^{\operatorname {\mathrm {Add}}(\omega ,\kappa )}$
:
$V^{\operatorname {\mathrm {Add}}(\omega ,\kappa )}$
:
-
(1)
 $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\omega ,2)$
holds
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\omega ,2)$
holds
 $;$
$;$
-
(2)
 $\operatorname {\mathrm {U}}(\kappa ,2,\omega ,\omega )$
holds
$\operatorname {\mathrm {U}}(\kappa ,2,\omega ,\omega )$
holds
 $;$
$;$
-
(3)
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
fails for every regular uncountable
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
fails for every regular uncountable
 $\theta <\kappa $
.
$\theta <\kappa $
.
Proof
-
(1) By [Reference Lambie-Hanson and Rinot20, Lemma 2.7].
-
(2) It is not hard to see that, in
 $V^{\operatorname {\mathrm {Add}}(\omega ,\kappa )}$
,
$V^{\operatorname {\mathrm {Add}}(\omega ,\kappa )}$
,
 $\operatorname {\mathrm {Pr}}_1(\kappa ,\omega _1,\omega ,\omega )$
holds. In particular, by [Reference Lambie-Hanson and Rinot20, Lemma 2.3],
$\operatorname {\mathrm {Pr}}_1(\kappa ,\omega _1,\omega ,\omega )$
holds. In particular, by [Reference Lambie-Hanson and Rinot20, Lemma 2.3],
 $\operatorname {\mathrm {U}}(\kappa ,2,\omega ,\omega )$
holds.
$\operatorname {\mathrm {U}}(\kappa ,2,\omega ,\omega )$
holds. -
(3) Evidently, for every
 $ccc$
forcing
$ccc$
forcing
 $\mathbb P$
and every infinite cardinal
$\mathbb P$
and every infinite cardinal
 $\theta $
,
$\theta $
,
 $\kappa \rightarrow [\kappa ]^2_{\theta }$
implies
$\kappa \rightarrow [\kappa ]^2_{\theta }$
implies
 $V^{\mathbb P}\models \kappa \rightarrow [\kappa ]^2_{\theta ,\omega }$
. In particular, in
$V^{\mathbb P}\models \kappa \rightarrow [\kappa ]^2_{\theta ,\omega }$
. In particular, in
 $V^{\operatorname {\mathrm {Add}}(\omega ,\kappa )}$
,
$V^{\operatorname {\mathrm {Add}}(\omega ,\kappa )}$
,
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
fails for every regular uncountable
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
fails for every regular uncountable
 $\theta <\kappa $
.
$\theta <\kappa $
.
3 Subadditive colorings
We now turn to subadditive colorings, which form the primary topic of this paper. We begin by recalling the definition of subadditivity, splitting the definition into its two constituent parts.
Definition 3.1. A coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
is subadditive iff the following two statements hold:
$c:[\kappa ]^2\rightarrow \theta $
is subadditive iff the following two statements hold:
-
(1) c is subadditive of the first kind, that is, for all
 $\alpha < \beta < \gamma < \kappa $
,
$\alpha < \beta < \gamma < \kappa $
,  $$ \begin{align*}c(\alpha, \gamma) \leq \max\{c(\alpha, \beta), c(\beta, \gamma)\}.\end{align*} $$
$$ \begin{align*}c(\alpha, \gamma) \leq \max\{c(\alpha, \beta), c(\beta, \gamma)\}.\end{align*} $$
-
(2) c is subadditive of the second kind, that is, for all
 $\alpha < \beta < \gamma < \kappa $
,
$\alpha < \beta < \gamma < \kappa $
,  $$ \begin{align*}c(\alpha, \beta) \leq \max\{c(\alpha, \gamma), c(\beta, \gamma)\}.\end{align*} $$
$$ \begin{align*}c(\alpha, \beta) \leq \max\{c(\alpha, \gamma), c(\beta, \gamma)\}.\end{align*} $$
We shall write
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \mu , \theta , \chi )$
to assert that
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \mu , \theta , \chi )$
to assert that
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
holds and that it moreover admits a subadditive witness. Note that the function
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
holds and that it moreover admits a subadditive witness. Note that the function
![]() $c:[\kappa ]^2 \rightarrow \kappa $
defined by letting
$c:[\kappa ]^2 \rightarrow \kappa $
defined by letting
![]() $c(\alpha , \beta ) := \alpha $
for all
$c(\alpha , \beta ) := \alpha $
for all
![]() $(\alpha , \beta ) \in [\kappa ]^2$
is a closed, subadditive witness to
$(\alpha , \beta ) \in [\kappa ]^2$
is a closed, subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa , \kappa , \kappa , \kappa )$
, so, in all situations of interest, we will have
$\operatorname {\mathrm {U}}(\kappa , \kappa , \kappa , \kappa )$
, so, in all situations of interest, we will have
![]() $\theta < \kappa $
.
$\theta < \kappa $
.
Subadditivity allows us to show that witnesses to certain instances of
![]() $\operatorname {\mathrm {U}}(\ldots )$
in fact satisfy stronger instances, as in the following lemma.
$\operatorname {\mathrm {U}}(\ldots )$
in fact satisfy stronger instances, as in the following lemma.
Lemma 3.2. Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
is a witness to
$c:[\kappa ]^2\rightarrow \theta $
is a witness to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
, with
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
, with
![]() $\theta <\kappa $
. Then the following statements all hold.
$\theta <\kappa $
. Then the following statements all hold.
-
(1) For every
 $\mu < \kappa $
, c witnesses
$\mu < \kappa $
, c witnesses
 $\operatorname {\mathrm {U}}(\kappa ,\mu ,\theta ,2)$
. If there exist no
$\operatorname {\mathrm {U}}(\kappa ,\mu ,\theta ,2)$
. If there exist no
 $\kappa $
-Souslin trees, then c moreover witnesses
$\kappa $
-Souslin trees, then c moreover witnesses
 $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,2)$
. -
(2) For every
 $\mu \le \kappa $
, if c witnesses
$\mu \le \kappa $
, if c witnesses
 $\operatorname {\mathrm {U}}(\kappa ,\mu ,\theta ,2)$
, then c moreover witnesses
$\operatorname {\mathrm {U}}(\kappa ,\mu ,\theta ,2)$
, then c moreover witnesses
 $\operatorname {\mathrm {U}}(\kappa ,\mu ,\theta ,\operatorname {\mathrm {cf}}(\theta ))$
.
$\operatorname {\mathrm {U}}(\kappa ,\mu ,\theta ,\operatorname {\mathrm {cf}}(\theta ))$
. -
(3) For every
 $\chi \in \operatorname {\mathrm {Reg}}(\kappa )$
, if c is
$\chi \in \operatorname {\mathrm {Reg}}(\kappa )$
, if c is
 $\Sigma $
-closed for some stationary
$\Sigma $
-closed for some stationary
 $\Sigma \subseteq E^{\kappa }_{\geq \chi }$
, then c witnesses
$\Sigma \subseteq E^{\kappa }_{\geq \chi }$
, then c witnesses
 $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\chi )$
.
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\chi )$
.
Proof For each
![]() $i<\theta $
, we define an ordering
$i<\theta $
, we define an ordering
![]() $<_i$
on
$<_i$
on
![]() $\kappa $
by letting
$\kappa $
by letting
![]() $\alpha <_i\beta $
iff
$\alpha <_i\beta $
iff
![]() $\alpha <\beta $
and
$\alpha <\beta $
and
![]() $c(\alpha ,\beta )\le i$
. The fact that
$c(\alpha ,\beta )\le i$
. The fact that
![]() $<_i$
is transitive follows from the fact that c is subadditive of the first kind.
$<_i$
is transitive follows from the fact that c is subadditive of the first kind.
Claim 3.2.1. For every
![]() $i<\theta $
,
$i<\theta $
,
![]() $(\kappa , <_i)$
is a tree with no branches of size
$(\kappa , <_i)$
is a tree with no branches of size
![]() $\kappa $
.
$\kappa $
.
Proof Let
![]() $i<\theta $
and
$i<\theta $
and
![]() $\gamma <\kappa $
. To see that set
$\gamma <\kappa $
. To see that set
![]() $\{\alpha <\kappa \mathrel {|} \alpha <_i\gamma \}$
is well-ordered by
$\{\alpha <\kappa \mathrel {|} \alpha <_i\gamma \}$
is well-ordered by
![]() $<_i$
, fix
$<_i$
, fix
![]() $\alpha < \beta $
such that
$\alpha < \beta $
such that
![]() $\alpha , \beta <_i \gamma $
. As c is subadditive of the second kind,
$\alpha , \beta <_i \gamma $
. As c is subadditive of the second kind,
![]() $c(\alpha ,\beta )\le \max \{c(\alpha ,\gamma ),c(\beta ,\gamma )\}\le i$
, so
$c(\alpha ,\beta )\le \max \{c(\alpha ,\gamma ),c(\beta ,\gamma )\}\le i$
, so
![]() $\alpha <_i\beta $
.
$\alpha <_i\beta $
.
In addition, by the hypothesis on c, for every
![]() $A\in [\kappa ]^{\kappa }$
, there is a pair
$A\in [\kappa ]^{\kappa }$
, there is a pair
![]() $(\alpha ,\beta )\in [A]^2$
such that
$(\alpha ,\beta )\in [A]^2$
such that
![]() $c(\alpha ,\beta )>i$
, so
$c(\alpha ,\beta )>i$
, so
![]() $\neg (\alpha <_i\beta )$
. That is,
$\neg (\alpha <_i\beta )$
. That is,
![]() $(\kappa ,<_i)$
has no chains of size
$(\kappa ,<_i)$
has no chains of size
![]() $\kappa $
.
$\kappa $
.
(1) Fix
![]() $\mu \le \kappa $
, and suppose that we are given some
$\mu \le \kappa $
, and suppose that we are given some
![]() $A\in [\kappa ]^{\kappa }$
and
$A\in [\kappa ]^{\kappa }$
and
![]() $i<\theta $
. We would like to find
$i<\theta $
. We would like to find
![]() $B\in [A]^{\mu }$
such that
$B\in [A]^{\mu }$
such that
![]() $c(\alpha ,\beta )>i$
for all
$c(\alpha ,\beta )>i$
for all
![]() $(\alpha ,\beta )\in [B]^2$
. In particular, if there exists
$(\alpha ,\beta )\in [B]^2$
. In particular, if there exists
![]() $B\in [\kappa ]^{\mu }$
which is an antichain with respect to
$B\in [\kappa ]^{\mu }$
which is an antichain with respect to
![]() $<_i$
, then we are done. Hereafter, suppose this is not the case.
$<_i$
, then we are done. Hereafter, suppose this is not the case.
-
▸ If
 $\mu <\kappa $
, then
$\mu <\kappa $
, then
 $(A,<_i)$
is a tree of size
$(A,<_i)$
is a tree of size
 $\kappa $
all of whose levels have size
$\kappa $
all of whose levels have size
 $<\mu $
. Since
$<\mu $
. Since
 $\mu <\kappa $
and
$\mu <\kappa $
and
 $\kappa $
is regular, a result of Kurepa [Reference Kurepa15] implies that
$\kappa $
is regular, a result of Kurepa [Reference Kurepa15] implies that
 $(\kappa ,<_i)$
has a branch of size
$(\kappa ,<_i)$
has a branch of size
 $\kappa $
, contradicting the preceding claim.
$\kappa $
, contradicting the preceding claim. -
▸ If
 $\mu =\kappa $
, then
$\mu =\kappa $
, then
 $(A,<_i)$
forms a
$(A,<_i)$
forms a
 $\kappa $
-Souslin tree.
$\kappa $
-Souslin tree.
(2) Suppose that
![]() $\mu \leq \kappa $
and c witnesses
$\mu \leq \kappa $
and c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , 2)$
. Suppose also that
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , 2)$
. Suppose also that
![]() $\mathcal A\subseteq [\kappa ]^{<\operatorname {\mathrm {cf}}(\theta )}$
consists of
$\mathcal A\subseteq [\kappa ]^{<\operatorname {\mathrm {cf}}(\theta )}$
consists of
![]() $\kappa $
-many pairwise disjoint sets and
$\kappa $
-many pairwise disjoint sets and
![]() $i<\theta $
is a prescribed color. We will find
$i<\theta $
is a prescribed color. We will find
![]() $\mathcal {B} \in [\mathcal {A}]^{\mu }$
such that
$\mathcal {B} \in [\mathcal {A}]^{\mu }$
such that
![]() $\min (c[a \times b])> i$
for all
$\min (c[a \times b])> i$
for all
![]() $(a,b) \in [\mathcal {B}]^2$
. For each
$(a,b) \in [\mathcal {B}]^2$
. For each
![]() $\gamma <\kappa $
, pick
$\gamma <\kappa $
, pick
![]() $a_{\gamma }\in \mathcal A$
with
$a_{\gamma }\in \mathcal A$
with
![]() $\gamma < a_{\gamma }$
. Define
$\gamma < a_{\gamma }$
. Define
![]() $f:\kappa \rightarrow \theta $
and
$f:\kappa \rightarrow \theta $
and
![]() $g:\kappa \rightarrow \kappa $
by setting, for all
$g:\kappa \rightarrow \kappa $
by setting, for all
![]() $\gamma < \kappa $
,
$\gamma < \kappa $
,
-
•
 $f(\gamma ):=\sup \{c(\gamma ,\alpha )\mathrel {|} \alpha \in a_{\gamma }\}$
;
$f(\gamma ):=\sup \{c(\gamma ,\alpha )\mathrel {|} \alpha \in a_{\gamma }\}$
; -
•
 $g(\gamma ):=\sup (a_{\gamma })$
.
$g(\gamma ):=\sup (a_{\gamma })$
.
Fix
![]() $\varepsilon <\theta $
for which
$\varepsilon <\theta $
for which
![]() $A:=\{ \gamma <\kappa \mathrel {|} f(\gamma )=\varepsilon \ \&\ g[\gamma ]\subseteq \gamma \}$
is stationary. Since c witnesses
$A:=\{ \gamma <\kappa \mathrel {|} f(\gamma )=\varepsilon \ \&\ g[\gamma ]\subseteq \gamma \}$
is stationary. Since c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,\mu ,\theta ,2)$
, we can pick
$\operatorname {\mathrm {U}}(\kappa ,\mu ,\theta ,2)$
, we can pick
![]() $B\in [A]^{\mu }$
such that
$B\in [A]^{\mu }$
such that
![]() $c(\gamma ,\delta )>\max \{\varepsilon ,i\}$
for all
$c(\gamma ,\delta )>\max \{\varepsilon ,i\}$
for all
![]() $(\gamma , \delta ) \in [B]^2$
. We claim that
$(\gamma , \delta ) \in [B]^2$
. We claim that
![]() $\mathcal B:=\{ a_{\gamma }\mathrel {|} \gamma \in B\}$
is a subfamily of
$\mathcal B:=\{ a_{\gamma }\mathrel {|} \gamma \in B\}$
is a subfamily of
![]() $\mathcal A$
as sought. To see this, pick a pair
$\mathcal A$
as sought. To see this, pick a pair
![]() $(\gamma ,\delta )\in [B]^2$
along with
$(\gamma ,\delta )\in [B]^2$
along with
![]() $(\alpha ,\beta )\in a_{\gamma }\times a_{\delta }$
. Clearly,
$(\alpha ,\beta )\in a_{\gamma }\times a_{\delta }$
. Clearly,
![]() $\gamma <\alpha <\delta <\beta $
. By the subadditivity of c and the choice of
$\gamma <\alpha <\delta <\beta $
. By the subadditivity of c and the choice of
![]() $\varepsilon $
, we have
$\varepsilon $
, we have
Recalling that
![]() $\max \{\varepsilon ,i\}<c(\gamma ,\delta )$
, we infer that
$\max \{\varepsilon ,i\}<c(\gamma ,\delta )$
, we infer that
![]() $i<c(\gamma ,\delta )\le c(\alpha ,\beta )$
, as sought.
$i<c(\gamma ,\delta )\le c(\alpha ,\beta )$
, as sought.
(3) Suppose that
![]() $\chi \in \operatorname {\mathrm {Reg}}(\kappa )$
,
$\chi \in \operatorname {\mathrm {Reg}}(\kappa )$
,
![]() $\Sigma \subseteq E^{\kappa }_{\geq \chi }$
is stationary, and c is
$\Sigma \subseteq E^{\kappa }_{\geq \chi }$
is stationary, and c is
![]() $\Sigma $
-closed.
$\Sigma $
-closed.
Claim 3.2.2. Suppose that
![]() $\mathcal A\subseteq [\kappa ]^{<\chi }$
is a family consisting of
$\mathcal A\subseteq [\kappa ]^{<\chi }$
is a family consisting of
![]() $\kappa $
-many pairwise disjoint sets, D is a club in
$\kappa $
-many pairwise disjoint sets, D is a club in
![]() $\kappa $
, and
$\kappa $
, and
![]() $i<\theta $
is a prescribed color. Then there exist
$i<\theta $
is a prescribed color. Then there exist
![]() $\gamma \in D \cap \Sigma $
and
$\gamma \in D \cap \Sigma $
and
![]() $a\in \mathcal A$
such that:
$a\in \mathcal A$
such that:
-
(a)
 $\gamma < a$
;
$\gamma < a$
; -
(b) for all
 $\beta \in a$
, we have
$\beta \in a$
, we have
 $c(\gamma ,\beta )>i$
.
$c(\gamma ,\beta )>i$
.
Proof Suppose not. Let
![]() $T := D \cap \Sigma $
, and note that, for all
$T := D \cap \Sigma $
, and note that, for all
![]() $\gamma \in T$
and all
$\gamma \in T$
and all
![]() $a\in \mathcal A$
with
$a\in \mathcal A$
with
![]() $a>\gamma $
, and for some
$a>\gamma $
, and for some
![]() $\beta \in a$
, we have
$\beta \in a$
, we have
![]() $c(\gamma ,\beta )\le i$
. Consider the tree
$c(\gamma ,\beta )\le i$
. Consider the tree
![]() $(T,<_i)$
. We claim that it has no antichains of size
$(T,<_i)$
. We claim that it has no antichains of size
![]() $\chi $
. To see this, fix an arbitrary
$\chi $
. To see this, fix an arbitrary
![]() $X\subseteq T$
of order type
$X\subseteq T$
of order type
![]() $\chi $
, and let
$\chi $
, and let
![]() $\delta :=\sup (X)$
. Fix an arbitrary
$\delta :=\sup (X)$
. Fix an arbitrary
![]() $a\in \mathcal A$
with
$a\in \mathcal A$
with
![]() $a> \delta $
. For all
$a> \delta $
. For all
![]() $\gamma \in X$
, since
$\gamma \in X$
, since
![]() $a>\gamma $
, we may find some
$a>\gamma $
, we may find some
![]() $\beta \in a$
with
$\beta \in a$
with
![]() $c(\gamma ,\beta )\le i$
. Since
$c(\gamma ,\beta )\le i$
. Since
![]() $|X|=\chi>|a|$
, we may then pick
$|X|=\chi>|a|$
, we may then pick
![]() $(\gamma , \gamma ') \in [X]^2$
and
$(\gamma , \gamma ') \in [X]^2$
and
![]() $\beta \in a$
such that
$\beta \in a$
such that
![]() $c(\gamma ,\beta )\le i$
and
$c(\gamma ,\beta )\le i$
and
![]() $c(\gamma ',\beta )\le i$
. It follows that
$c(\gamma ',\beta )\le i$
. It follows that
![]() $c(\gamma ,\gamma ')\le \max \{c(\gamma ,\beta ),c(\gamma ',\beta )\}\le i$
. In particular, X is not an antichain. Now, since
$c(\gamma ,\gamma ')\le \max \{c(\gamma ,\beta ),c(\gamma ',\beta )\}\le i$
. In particular, X is not an antichain. Now, since
![]() $\chi <\kappa $
are regular cardinals, the aforementioned result of Kurepa [Reference Kurepa15] entails the existence of
$\chi <\kappa $
are regular cardinals, the aforementioned result of Kurepa [Reference Kurepa15] entails the existence of
![]() $B\in [T]^{\kappa }$
which is a chain with respect to
$B\in [T]^{\kappa }$
which is a chain with respect to
![]() $<_i$
. By the hypothesis on c, we can pick
$<_i$
. By the hypothesis on c, we can pick
![]() $(\alpha , \beta ) \in [B]^2$
such that
$(\alpha , \beta ) \in [B]^2$
such that
![]() $c(\alpha ,\beta )>i$
. Then
$c(\alpha ,\beta )>i$
. Then
![]() $\neg (\alpha <_i\beta )$
which is a contradiction to the fact that B is a chain in
$\neg (\alpha <_i\beta )$
which is a contradiction to the fact that B is a chain in
![]() $(T,<_i)$
.
$(T,<_i)$
.
As c is
![]() $\Sigma $
-closed and
$\Sigma $
-closed and
![]() $\Sigma \subseteq E^{\kappa }_{\geq \chi }$
, Clause (b) of the preceding is equivalent to:
$\Sigma \subseteq E^{\kappa }_{\geq \chi }$
, Clause (b) of the preceding is equivalent to:
-
(b’) there is
 $\epsilon < \gamma $
such that, for all
$\epsilon < \gamma $
such that, for all
 $\alpha \in (\epsilon , \gamma )$
and all
$\alpha \in (\epsilon , \gamma )$
and all
 $\beta \in a$
, we have
$\beta \in a$
, we have
 $c(\alpha ,\beta )>i$
.
$c(\alpha ,\beta )>i$
.
Thus, by the implication
![]() $(2)\implies (3)$
of Fact 2.2, we can conclude that c witnesses
$(2)\implies (3)$
of Fact 2.2, we can conclude that c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \chi )$
, as desired.
$\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \chi )$
, as desired.
3.1 Narrow systems and trees with ascent paths
Given a binary relation R on a set X, for
![]() $a,b \in X$
, we say that a and b are R-comparable iff
$a,b \in X$
, we say that a and b are R-comparable iff
![]() $a = b$
,
$a = b$
,
![]() $a \mathrel {R} b$
, or
$a \mathrel {R} b$
, or
![]() $b \mathrel {R} a$
. R is tree-like iff, for all
$b \mathrel {R} a$
. R is tree-like iff, for all
![]() $a,b,c \in X$
, if
$a,b,c \in X$
, if
![]() $a \mathrel {R} c$
and
$a \mathrel {R} c$
and
![]() $b \mathrel {R} c$
, then a and b are R-comparable.
$b \mathrel {R} c$
, then a and b are R-comparable.
Definition 3.3 (Magidor–Shelah [Reference Moore25]).
![]() $S = \langle \bigcup _{\alpha \in I}\{\alpha \} \times \theta _{\alpha }, \mathcal {R} \rangle $
is a
$S = \langle \bigcup _{\alpha \in I}\{\alpha \} \times \theta _{\alpha }, \mathcal {R} \rangle $
is a
![]() $\kappa $
-system if all of the following hold:
$\kappa $
-system if all of the following hold:
-
(1)
 $I \subseteq \kappa $
is unbounded and, for all
$I \subseteq \kappa $
is unbounded and, for all
 $\alpha \in I$
,
$\alpha \in I$
,
 $\theta _{\alpha }$
is a cardinal such that
$\theta _{\alpha }$
is a cardinal such that
 $0 < \theta _{\alpha } < \kappa $
.
$0 < \theta _{\alpha } < \kappa $
. -
(2)
 $\mathcal {R}$
is a set of binary, transitive, tree-like relations on
$\mathcal {R}$
is a set of binary, transitive, tree-like relations on
 $\bigcup _{\alpha \in I}\{\alpha \} \times \theta _{\alpha }$
and
$\bigcup _{\alpha \in I}\{\alpha \} \times \theta _{\alpha }$
and
 $0 < |\mathcal {R}| < \kappa $
.
$0 < |\mathcal {R}| < \kappa $
. -
(3) For all
 $R \in \mathcal {R}$
,
$R \in \mathcal {R}$
,
 $\alpha _0, \alpha _1 \in I$
,
$\alpha _0, \alpha _1 \in I$
,
 $\beta _0 < \theta _{\alpha _0}$
, and
$\beta _0 < \theta _{\alpha _0}$
, and
 $\beta _1 < \theta _{\alpha _1}$
, if
$\beta _1 < \theta _{\alpha _1}$
, if
 $(\alpha _0, \beta _0) \mathrel {R} (\alpha _1,\beta _1)$
, then
$(\alpha _0, \beta _0) \mathrel {R} (\alpha _1,\beta _1)$
, then
 $\alpha _0 < \alpha _1$
.
$\alpha _0 < \alpha _1$
. -
(4) For every
 $(\alpha _0,\alpha _1)\in [I]^2$
, there are
$(\alpha _0,\alpha _1)\in [I]^2$
, there are
 $(\beta _0,\beta _1)\in \theta _{\alpha _0}\times \theta _{\alpha _1}$
and
$(\beta _0,\beta _1)\in \theta _{\alpha _0}\times \theta _{\alpha _1}$
and
 $R \in \mathcal {R}$
such that
$R \in \mathcal {R}$
such that
 $(\alpha _0, \beta _0) \mathrel {R} (\alpha _1, \beta _1)$
.
$(\alpha _0, \beta _0) \mathrel {R} (\alpha _1, \beta _1)$
.
Define
![]() $\mathrm {width}(S) := \sup \{|\mathcal {R}|,\theta _{\alpha } \mathrel {|} \alpha \in I\}$
. A
$\mathrm {width}(S) := \sup \{|\mathcal {R}|,\theta _{\alpha } \mathrel {|} \alpha \in I\}$
. A
![]() $\kappa $
-system S is narrow if
$\kappa $
-system S is narrow if
![]() $\mathrm {width}(S)^+ < \kappa $
. For
$\mathrm {width}(S)^+ < \kappa $
. For
![]() $R \in \mathcal {R}$
, a branch of S through R is a set
$R \in \mathcal {R}$
, a branch of S through R is a set
![]() $B\subseteq \bigcup _{\alpha \in I}\{\alpha \} \times \theta _{\alpha }$
such that for all
$B\subseteq \bigcup _{\alpha \in I}\{\alpha \} \times \theta _{\alpha }$
such that for all
![]() $a,b \in B$
, a and b are R-comparable. A branch B is cofinal iff
$a,b \in B$
, a and b are R-comparable. A branch B is cofinal iff
![]() $\sup \{ \alpha \in I\mathrel {|} \exists \tau <\theta _{\alpha }~(\alpha ,\tau )\in B\}=\kappa $
.
$\sup \{ \alpha \in I\mathrel {|} \exists \tau <\theta _{\alpha }~(\alpha ,\tau )\in B\}=\kappa $
.
Definition 3.4 [Reference Lambie-Hanson17].
The
![]() $(\theta , \kappa )$
-narrow system property, which is abbreviated
$(\theta , \kappa )$
-narrow system property, which is abbreviated
![]() $\textsf{NSP}(\theta , \kappa )$
, asserts that every narrow
$\textsf{NSP}(\theta , \kappa )$
, asserts that every narrow
![]() $\kappa $
-system of width
$\kappa $
-system of width
![]() $< \theta $
has a cofinal branch.
$< \theta $
has a cofinal branch.
By [Reference Lambie-Hanson17, Section 10],
![]() $\textsf {PFA}$
implies
$\textsf {PFA}$
implies
![]() $\textsf{NSP}(\omega _1, \kappa )$
for all regular
$\textsf{NSP}(\omega _1, \kappa )$
for all regular
![]() $\kappa \ge \omega _2$
.
$\kappa \ge \omega _2$
.
Lemma 3.5. Suppose that
![]() $\theta <\theta ^+<\kappa $
and
$\theta <\theta ^+<\kappa $
and
![]() $c:[\kappa ]^2\rightarrow \theta $
is a subadditive coloring. If
$c:[\kappa ]^2\rightarrow \theta $
is a subadditive coloring. If
![]() $\textsf{NSP}(\theta ^+,\kappa )$
holds, then c fails to witness
$\textsf{NSP}(\theta ^+,\kappa )$
holds, then c fails to witness
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
Proof Define a binary relation
![]() $ R$
on
$ R$
on
![]() $\kappa \times \theta $
by letting
$\kappa \times \theta $
by letting
![]() $(\alpha ,i)\mathrel {R}(\beta ,j)$
iff
$(\alpha ,i)\mathrel {R}(\beta ,j)$
iff
![]() $\alpha <\beta $
,
$\alpha <\beta $
,
![]() $i=j$
, and
$i=j$
, and
![]() $c(\alpha ,\beta )\le i$
.
$c(\alpha ,\beta )\le i$
.
Claim 3.5.1. Let
![]() $\alpha <\beta <\gamma <\kappa $
. Then:
$\alpha <\beta <\gamma <\kappa $
. Then:
-
(1) there exists
 $i<\theta $
such that
$i<\theta $
such that
 $(\alpha ,i)\mathrel {R}(\beta ,i)$
;
$(\alpha ,i)\mathrel {R}(\beta ,i)$
; -
(2) for all
 $i<\theta $
, if
$i<\theta $
, if
 $(\alpha ,i)\mathrel {R}(\beta ,i)$
and
$(\alpha ,i)\mathrel {R}(\beta ,i)$
and
 $(\beta ,i)\mathrel {R}(\gamma ,i)$
, then
$(\beta ,i)\mathrel {R}(\gamma ,i)$
, then
 $(\alpha ,i)\mathrel {R}(\gamma ,i)$
;
$(\alpha ,i)\mathrel {R}(\gamma ,i)$
; -
(3) for all
 $i<\theta $
, if
$i<\theta $
, if
 $(\alpha ,i)\mathrel {R}(\gamma ,i)$
and
$(\alpha ,i)\mathrel {R}(\gamma ,i)$
and
 $(\beta ,i)\mathrel {R}(\gamma ,i)$
, then
$(\beta ,i)\mathrel {R}(\gamma ,i)$
, then
 $(\alpha ,i)\mathrel {R}(\beta ,i)$
.
$(\alpha ,i)\mathrel {R}(\beta ,i)$
.
Proof
-
(1) Just take
 $i:=c(\alpha ,\beta )$
.
$i:=c(\alpha ,\beta )$
. -
(2) By subadditivity of the first kind.
-
(3) By subadditivity of the second kind.
It thus follows that
![]() $S:=\langle \kappa \times \theta ,\{R\}\rangle $
is a narrow
$S:=\langle \kappa \times \theta ,\{R\}\rangle $
is a narrow
![]() $\kappa $
-system. So, assuming that
$\kappa $
-system. So, assuming that
![]() $\textsf{NSP}(\theta ^+,\kappa )$
holds, we may fix
$\textsf{NSP}(\theta ^+,\kappa )$
holds, we may fix
![]() $B\subseteq \kappa \times \theta $
that forms a cofinal branch of S through R. Pick
$B\subseteq \kappa \times \theta $
that forms a cofinal branch of S through R. Pick
![]() $A\in [\kappa ]^{\kappa }$
and
$A\in [\kappa ]^{\kappa }$
and
![]() $i<\theta $
such that
$i<\theta $
such that
![]() $B=A\times \{i\}$
. Now, if c were to witness
$B=A\times \{i\}$
. Now, if c were to witness
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, then we could fix
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, then we could fix
![]() $(\alpha ,\beta )\in [A]^2$
such that
$(\alpha ,\beta )\in [A]^2$
such that
![]() $c(\alpha ,\beta )>i$
. But then
$c(\alpha ,\beta )>i$
. But then
![]() $(\alpha ,i)\mathrel {R}(\beta ,i)$
would fail to hold, contradicting the fact that
$(\alpha ,i)\mathrel {R}(\beta ,i)$
would fail to hold, contradicting the fact that
![]() $\{(\alpha ,i),(\beta ,i)\}\subseteq B$
.
$\{(\alpha ,i),(\beta ,i)\}\subseteq B$
.
Next, we prove a pair of lemmas establishing an equivalency between instances of
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\ldots )$
and the existence of trees with ascent paths but no cofinal branches. We first recall the following definition.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\ldots )$
and the existence of trees with ascent paths but no cofinal branches. We first recall the following definition.
Definition 3.6. Suppose that
![]() $\mathcal {T} = (T, <_T)$
is a tree of height
$\mathcal {T} = (T, <_T)$
is a tree of height
![]() $\kappa $
.
$\kappa $
.
-
(1) For all
 $\alpha < \kappa $
,
$\alpha < \kappa $
,
 $T_{\alpha }$
denotes level
$T_{\alpha }$
denotes level
 $\alpha $
of
$\alpha $
of
 $\mathcal {T}$
.
$\mathcal {T}$
. -
(2) A
 $\theta $
-ascent path through
$\theta $
-ascent path through
 $\mathcal {T}$
is a sequence of functions
$\mathcal {T}$
is a sequence of functions
 $\langle f_{\alpha } \mathrel {|} \alpha < \kappa \rangle $
such that:
$\langle f_{\alpha } \mathrel {|} \alpha < \kappa \rangle $
such that:-
(a) for all
 $\alpha < \kappa $
,
$\alpha < \kappa $
,
 $f_{\alpha }:\theta \rightarrow T_{\alpha }$
;
$f_{\alpha }:\theta \rightarrow T_{\alpha }$
; -
(b) for all
 $\alpha < \beta < \kappa $
, there is
$\alpha < \beta < \kappa $
, there is
 $i < \theta $
such that, for all
$i < \theta $
such that, for all
 $j \in [i, \theta )$
, we have
$j \in [i, \theta )$
, we have
 $f_{\alpha }(j) <_T f_{\beta }(j)$
.
$f_{\alpha }(j) <_T f_{\beta }(j)$
.
-
Lemma 3.7. Suppose that
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
, and
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
, and
![]() $\mathcal T$
is a tree of height
$\mathcal T$
is a tree of height
![]() $\kappa $
admitting a
$\kappa $
admitting a
![]() $\theta $
-ascent path but no branch of size
$\theta $
-ascent path but no branch of size
![]() $\kappa $
. Then
$\kappa $
. Then
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
holds.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
holds.
Proof Write
![]() $\mathcal T$
as
$\mathcal T$
as
![]() $(T,<_T)$
. Fix a
$(T,<_T)$
. Fix a
![]() $\theta $
-ascent path
$\theta $
-ascent path
![]() $\langle f_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
through
$\langle f_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
through
![]() $\mathcal T$
, and derive a coloring
$\mathcal T$
, and derive a coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
via
$c:[\kappa ]^2\rightarrow \theta $
via
We shall show that c witnesses
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
.
Claim 3.7.1. c is subadditive.
Proof Suppose that
![]() $\alpha <\beta <\gamma <\kappa $
.
$\alpha <\beta <\gamma <\kappa $
.
-
▸ Let
 $i:=\max \{c(\alpha ,\beta ),c(\beta ,\gamma )\}$
. Then, for all
$i:=\max \{c(\alpha ,\beta ),c(\beta ,\gamma )\}$
. Then, for all
 $j\in [i,\theta )$
, we have and hence
$j\in [i,\theta )$
, we have and hence $$\begin{align*}f_{\alpha}(j)<_T f_{\beta}(j)<_T f_{\gamma}(j), \end{align*}$$
$$\begin{align*}f_{\alpha}(j)<_T f_{\beta}(j)<_T f_{\gamma}(j), \end{align*}$$
 $f_{\alpha }(j)<_T f_{\gamma }(j)$
. Consequently,
$f_{\alpha }(j)<_T f_{\gamma }(j)$
. Consequently,
 $c(\alpha ,\gamma )\le i$
.
$c(\alpha ,\gamma )\le i$
.
-
▸ Let
 $i:=\max \{c(\alpha ,\gamma ),c(\beta ,\gamma )\}$
. Then, for all
$i:=\max \{c(\alpha ,\gamma ),c(\beta ,\gamma )\}$
. Then, for all
 $j\in [i,\theta )$
, we have
$j\in [i,\theta )$
, we have
 $f_{\alpha }(j)<_T f_{\gamma }(j)$
and
$f_{\alpha }(j)<_T f_{\gamma }(j)$
and
 $f_{\beta }(j)<_T f_{\gamma }(j)$
. But
$f_{\beta }(j)<_T f_{\gamma }(j)$
. But
 $\mathcal T$
is a tree, and hence
$\mathcal T$
is a tree, and hence
 $f_{\alpha }(j)<_T f_{\beta }(j)$
. Consequently,
$f_{\alpha }(j)<_T f_{\beta }(j)$
. Consequently,
 $c(\alpha ,\beta )\le i$
.
$c(\alpha ,\beta )\le i$
.
By Lemma 3.2, it remains to verify that c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. Suppose this is not the case. Then for some
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. Suppose this is not the case. Then for some
![]() $A\in [\kappa ]^{\kappa }$
,
$A\in [\kappa ]^{\kappa }$
,
![]() $i:=\sup (c"[A]^2)$
is
$i:=\sup (c"[A]^2)$
is
![]() $<\theta $
. But then the
$<\theta $
. But then the
![]() $<_T$
-downward closure of
$<_T$
-downward closure of
![]() $\{f_{\alpha }(i) \mathrel {|} \alpha \in A\}$
is a branch of size
$\{f_{\alpha }(i) \mathrel {|} \alpha \in A\}$
is a branch of size
![]() $\kappa $
through
$\kappa $
through
![]() $\mathcal T$
, contradicting our assumptions.
$\mathcal T$
, contradicting our assumptions.
We now prove the converse.
Lemma 3.8. Suppose that
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
and
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
and
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
holds. Then there exists a tree
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
holds. Then there exists a tree
![]() $\mathcal T$
of height
$\mathcal T$
of height
![]() $\kappa $
admitting a
$\kappa $
admitting a
![]() $\theta $
-ascent path but no branch of size
$\theta $
-ascent path but no branch of size
![]() $\kappa $
.
$\kappa $
.
Proof Let
![]() $c:[\kappa ]^2\rightarrow \theta $
be a witness for
$c:[\kappa ]^2\rightarrow \theta $
be a witness for
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
. First, put
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
. First, put
and then let
![]() $(i,\alpha ,\beta )<_T (i',\alpha ',\beta ')$
iff
$(i,\alpha ,\beta )<_T (i',\alpha ',\beta ')$
iff
![]() $i=i'$
,
$i=i'$
,
![]() $\alpha <\alpha '$
and either
$\alpha <\alpha '$
and either
![]() $\beta =\beta '$
or
$\beta =\beta '$
or
![]() $\beta <\beta '$
, and
$\beta <\beta '$
, and
![]() $c(\beta ,\beta ')\le i$
. Finally, let
$c(\beta ,\beta ')\le i$
. Finally, let
![]() $\mathcal T:=(T,<_T)$
.
$\mathcal T:=(T,<_T)$
.
Claim 3.8.1.
![]() $\mathcal T$
is a tree.
$\mathcal T$
is a tree.
Proof It is clear that
![]() $<_T$
is anti-symmetric. To see that
$<_T$
is anti-symmetric. To see that
![]() $<_T$
is transitive, suppose that
$<_T$
is transitive, suppose that
![]() $(i_0,\alpha _0,\beta _0)<_T(i_1,\alpha _1,\beta _1)$
and
$(i_0,\alpha _0,\beta _0)<_T(i_1,\alpha _1,\beta _1)$
and
![]() $(i_1,\alpha _1,\beta _1)<_T(i_2,\alpha _2,\beta _2)$
. Then
$(i_1,\alpha _1,\beta _1)<_T(i_2,\alpha _2,\beta _2)$
. Then
![]() $i_0=i_1=i_2$
and
$i_0=i_1=i_2$
and
![]() $\alpha _0<\alpha _1<\alpha _2$
. Now, if
$\alpha _0<\alpha _1<\alpha _2$
. Now, if
![]() $\beta _1\in \{\beta _0,\beta _2\}$
, then clearly
$\beta _1\in \{\beta _0,\beta _2\}$
, then clearly
![]() $(i_0,\alpha _0,\beta _0)<_T(i_2,\alpha _2,\beta _2)$
. Otherwise
$(i_0,\alpha _0,\beta _0)<_T(i_2,\alpha _2,\beta _2)$
. Otherwise
![]() $\beta _0<\beta _1<\beta _2$
and
$\beta _0<\beta _1<\beta _2$
and
![]() $c(\beta _0,\beta _2)\le \max \{c(\beta _0,\beta _1),c(\beta _1,\beta _2)\}\le i_0$
, as sought.
$c(\beta _0,\beta _2)\le \max \{c(\beta _0,\beta _1),c(\beta _1,\beta _2)\}\le i_0$
, as sought.
It is clear that
![]() $<_T$
is well-founded, so to see that
$<_T$
is well-founded, so to see that
![]() $<_T$
is a tree ordering, suppose that
$<_T$
is a tree ordering, suppose that
![]() $(i_0,\alpha _0,\beta _0)<_T(i_2,\alpha _2,\beta _2)$
and
$(i_0,\alpha _0,\beta _0)<_T(i_2,\alpha _2,\beta _2)$
and
![]() $(i_1,\alpha _1,\beta _1)<(i_2,\alpha _2,\beta _2)$
. Then
$(i_1,\alpha _1,\beta _1)<(i_2,\alpha _2,\beta _2)$
. Then
![]() $i_0=i_2=i_1$
and to avoid trivialities, we may also assume that
$i_0=i_2=i_1$
and to avoid trivialities, we may also assume that
![]() $|\{\beta _0,\beta _1,\beta _2\}|=3$
, say,
$|\{\beta _0,\beta _1,\beta _2\}|=3$
, say,
![]() $\beta _0<\beta _1<\beta _2$
. But then
$\beta _0<\beta _1<\beta _2$
. But then
![]() $c(\beta _0,\beta _1)\le \max \{c(\beta _0,\beta _2),c(\beta _1,\beta _2)\}\le i$
, as sought.
$c(\beta _0,\beta _1)\le \max \{c(\beta _0,\beta _2),c(\beta _1,\beta _2)\}\le i$
, as sought.
Claim 3.8.2. For every
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $T_{\alpha }:=\{ (i,\epsilon ,\beta )\in T\mathrel {|} \epsilon =\alpha \}$
is nonempty and constitutes the
$T_{\alpha }:=\{ (i,\epsilon ,\beta )\in T\mathrel {|} \epsilon =\alpha \}$
is nonempty and constitutes the
![]() $\alpha ^{th}$
-level of
$\alpha ^{th}$
-level of
![]() $\mathcal T$
.
$\mathcal T$
.
Proof By induction on
![]() $\alpha <\kappa $
.
$\alpha <\kappa $
.
-
▸ For any set of ordinals x,
 $\operatorname {\mathrm {ssup}}(x)=0$
iff x is empty, and hence
$\operatorname {\mathrm {ssup}}(x)=0$
iff x is empty, and hence
 $\{ (i,0,0)\mathrel {|} i<\theta \}\subseteq T_0$
. In addition, it is clear that any element of T of the form
$\{ (i,0,0)\mathrel {|} i<\theta \}\subseteq T_0$
. In addition, it is clear that any element of T of the form
 $(i,0,\beta )$
is minimal in
$(i,0,\beta )$
is minimal in
 $\mathcal T$
.
$\mathcal T$
. -
▸ For every
 $\alpha <\kappa $
such that
$\alpha <\kappa $
such that
 $T_{\alpha }$
constitutes the
$T_{\alpha }$
constitutes the
 $\alpha ^{th}$
-level of
$\alpha ^{th}$
-level of
 $\mathcal T$
, given
$\mathcal T$
, given
 $(i,\alpha +1,\beta )\in T_{\alpha +1}$
, we shall find an immediate predecessor of it, lying in
$(i,\alpha +1,\beta )\in T_{\alpha +1}$
, we shall find an immediate predecessor of it, lying in
 $T_{\alpha }$
. There are two cases to consider:
$T_{\alpha }$
. There are two cases to consider:-
▸▸ If
 $(i,\alpha ,\beta )$
is in T, then it is clearly an immediate predecessor of
$(i,\alpha ,\beta )$
is in T, then it is clearly an immediate predecessor of
 $(i,\alpha +1,\beta )$
.
$(i,\alpha +1,\beta )$
. -
▸▸ Otherwise, we have
 $\alpha < \operatorname {\mathrm {ssup}}(D^c_{\le i}(\beta )) \leq \alpha +1$
, i.e.,
$\alpha < \operatorname {\mathrm {ssup}}(D^c_{\le i}(\beta )) \leq \alpha +1$
, i.e.,
 $\operatorname {\mathrm {ssup}}(D^c_{\le i}(\beta )) = \alpha + 1$
, so
$\operatorname {\mathrm {ssup}}(D^c_{\le i}(\beta )) = \alpha + 1$
, so
 $\alpha = \max (D^c_{\le i}(\beta ))$
. Therefore,
$\alpha = \max (D^c_{\le i}(\beta ))$
. Therefore,
 $(i, \alpha , \alpha )$
is an immediate predecessor of
$(i, \alpha , \alpha )$
is an immediate predecessor of
 $(i, \alpha +1, \beta )$
.
$(i, \alpha +1, \beta )$
.
-
-
▸ For every
 $\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
such that, for every
$\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
such that, for every
 $\bar \alpha <\alpha $
,
$\bar \alpha <\alpha $
,
 $T_{\bar \alpha }$
constitutes the
$T_{\bar \alpha }$
constitutes the
 $\bar \alpha ^{th}$
-level of
$\bar \alpha ^{th}$
-level of
 $\mathcal T$
, given
$\mathcal T$
, given
 $(i,\alpha ,\beta )\in T_{\alpha }$
, we shall show that for every
$(i,\alpha ,\beta )\in T_{\alpha }$
, we shall show that for every
 $\bar \alpha <\alpha $
, there is
$\bar \alpha <\alpha $
, there is
 $\bar \beta \leq \beta $
such that
$\bar \beta \leq \beta $
such that
 $(i,\bar \alpha ,\bar \beta )$
belongs to T and is
$(i,\bar \alpha ,\bar \beta )$
belongs to T and is
 $<_T$
-below
$<_T$
-below
 $(i,\alpha ,\beta )$
.
$(i,\alpha ,\beta )$
.-
▸▸ If
 $(i,\bar \alpha ,\beta )$
is in T, then
$(i,\bar \alpha ,\beta )$
is in T, then
 $(i,\bar \alpha ,\beta )<_T(i,\alpha ,\beta )$
, and we are done.
$(i,\bar \alpha ,\beta )<_T(i,\alpha ,\beta )$
, and we are done. -
▸▸ Otherwise,
 $\operatorname {\mathrm {ssup}}(D^c_{\le i}(\beta ))> \bar {\alpha }$
. Let
$\operatorname {\mathrm {ssup}}(D^c_{\le i}(\beta ))> \bar {\alpha }$
. Let
 $\bar {\beta } := \min (D^c_{\le i}(\beta ) \setminus \bar {\alpha })$
. Since c is subadditive, we have
$\bar {\beta } := \min (D^c_{\le i}(\beta ) \setminus \bar {\alpha })$
. Since c is subadditive, we have
 $D^c_{\le i}(\bar {\beta }) = D^c_{\le i}(\beta ) \cap \bar {\beta }$
, and hence, by our choice of
$D^c_{\le i}(\bar {\beta }) = D^c_{\le i}(\beta ) \cap \bar {\beta }$
, and hence, by our choice of
 $\bar {\beta }$
, it follows that
$\bar {\beta }$
, it follows that
 $\operatorname {\mathrm {ssup}}(D^c_{\le i}(\bar {\beta })) \leq \alpha $
. Therefore,
$\operatorname {\mathrm {ssup}}(D^c_{\le i}(\bar {\beta })) \leq \alpha $
. Therefore,
 $(i,\bar \alpha ,\bar \beta )\in T$
and
$(i,\bar \alpha ,\bar \beta )\in T$
and
 $(i,\bar \alpha ,\bar \beta )<_T(i,\alpha ,\beta )$
.
$(i,\bar \alpha ,\bar \beta )<_T(i,\alpha ,\beta )$
.
-
The fact that
![]() ${\mathcal T}$
has no branch of size
${\mathcal T}$
has no branch of size
![]() $\kappa $
follows immediately from the fact that c witnesses
$\kappa $
follows immediately from the fact that c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, as in the proof of Claim 3.2.1. Finally, to see that
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, as in the proof of Claim 3.2.1. Finally, to see that
![]() $\mathcal T$
admits a
$\mathcal T$
admits a
![]() $\theta $
-ascent path, for every
$\theta $
-ascent path, for every
![]() $\alpha $
, define
$\alpha $
, define
![]() $f_{\alpha }:\theta \rightarrow T_{\alpha }$
by letting
$f_{\alpha }:\theta \rightarrow T_{\alpha }$
by letting
![]() $f_{\alpha }(i):=(i,\alpha ,\alpha )$
.
$f_{\alpha }(i):=(i,\alpha ,\alpha )$
.
Under an additional assumption, we may infer the existence of a tree with the preceding features that is moreover
![]() $\kappa $
-Aronszajn. Before stating the next result, we recall the notion of a C-sequence, which will be used in its proof.
$\kappa $
-Aronszajn. Before stating the next result, we recall the notion of a C-sequence, which will be used in its proof.
Definition 3.9. A C-sequence over
![]() $\kappa $
is a sequence
$\kappa $
is a sequence
![]() $\langle C_{\beta } \mathrel {|} \beta < \kappa \rangle $
such that, for all
$\langle C_{\beta } \mathrel {|} \beta < \kappa \rangle $
such that, for all
![]() $\beta < \kappa $
,
$\beta < \kappa $
,
![]() $C_{\beta }$
is a closed subset of
$C_{\beta }$
is a closed subset of
![]() $\beta $
with
$\beta $
with
![]() $\sup (C_{\beta }) = \sup (\beta )$
.
$\sup (C_{\beta }) = \sup (\beta )$
.
Lemma 3.10. Suppose that
![]() $\theta \le \chi \le \kappa $
are infinite regular cardinals such that
$\theta \le \chi \le \kappa $
are infinite regular cardinals such that
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\chi $
-inaccessible and
${<}\chi $
-inaccessible and
![]() $\theta <\kappa $
. If there exists an
$\theta <\kappa $
. If there exists an
![]() $E^{\kappa }_{\ge \chi }$
-closed witness to
$E^{\kappa }_{\ge \chi }$
-closed witness to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2,\theta ,\theta )$
, then there exists a
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2,\theta ,\theta )$
, then there exists a
![]() $\kappa $
-Aronszajn tree
$\kappa $
-Aronszajn tree
![]() $\mathcal T$
admitting a
$\mathcal T$
admitting a
![]() $\theta $
-ascent path.
$\theta $
-ascent path.
Proof As there is an
![]() $\omega _1$
-Aronszajn tree, and as any
$\omega _1$
-Aronszajn tree, and as any
![]() $\omega _1$
-Aronszajn tree admits an
$\omega _1$
-Aronszajn tree admits an
![]() $\omega $
-ascent path, we may assume that
$\omega $
-ascent path, we may assume that
![]() $\kappa \ge \aleph _2$
. Fix an
$\kappa \ge \aleph _2$
. Fix an
![]() $E^{\kappa }_{\ge \chi }$
-closed coloring
$E^{\kappa }_{\ge \chi }$
-closed coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
witnessing
$c:[\kappa ]^2\rightarrow \theta $
witnessing
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
. For every
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
. For every
![]() $\beta \in \operatorname {\mathrm {acc}}(\kappa )$
, let
$\beta \in \operatorname {\mathrm {acc}}(\kappa )$
, let
![]() $i(\beta )$
denote the least
$i(\beta )$
denote the least
![]() $i\le \theta $
such that
$i\le \theta $
such that
![]() $\sup (D^c_{\le i}(\beta ))=\beta $
. Note that if
$\sup (D^c_{\le i}(\beta ))=\beta $
. Note that if
![]() $\operatorname {\mathrm {cf}}(\beta )\neq \theta $
, then
$\operatorname {\mathrm {cf}}(\beta )\neq \theta $
, then
![]() $i(\beta )<\theta $
. Now, for every
$i(\beta )<\theta $
. Now, for every
![]() $i<\theta $
, define a C-sequence
$i<\theta $
, define a C-sequence
![]() $\vec C^i:=\langle C_{\beta }^i\mathrel {|} \beta <\kappa \rangle $
as follows.
$\vec C^i:=\langle C_{\beta }^i\mathrel {|} \beta <\kappa \rangle $
as follows.
-
▸ Let
 $C^i_0:=\emptyset $
.
$C^i_0:=\emptyset $
. -
▸ For all
 $\beta <\kappa $
, let
$\beta <\kappa $
, let
 $C_{\beta +1}^i:=\{\beta \}$
.
$C_{\beta +1}^i:=\{\beta \}$
. -
▸ For all
 $\beta \in \operatorname {\mathrm {acc}}(\kappa )$
such that
$\beta \in \operatorname {\mathrm {acc}}(\kappa )$
such that
 $i\ge i(\beta )$
, let
$i\ge i(\beta )$
, let
 $C_{\beta }^i:=\operatorname {\mathrm {cl}}(D^c_{\le i}(\beta ))$
.
$C_{\beta }^i:=\operatorname {\mathrm {cl}}(D^c_{\le i}(\beta ))$
. -
▸ For all
 $\beta \in \operatorname {\mathrm {acc}}(\kappa )$
such that
$\beta \in \operatorname {\mathrm {acc}}(\kappa )$
such that
 $i<i(\beta )<\theta $
, let
$i<i(\beta )<\theta $
, let
 $C_{\beta }^i:=\operatorname {\mathrm {cl}}(D^c_{\le i(\beta )}(\beta ))$
.
$C_{\beta }^i:=\operatorname {\mathrm {cl}}(D^c_{\le i(\beta )}(\beta ))$
. -
▸ For any other
 $\beta $
, let
$\beta $
, let
 $C^i_{\beta }$
be a club in
$C^i_{\beta }$
be a club in
 $\beta $
of order-type
$\beta $
of order-type
 $\theta $
.
$\theta $
.
Claim 3.10.1. For every
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $|\{ C^i_{\beta }\cap \alpha \mathrel {|} \beta <\kappa , ~ i<\theta \}|<\kappa $
.
$|\{ C^i_{\beta }\cap \alpha \mathrel {|} \beta <\kappa , ~ i<\theta \}|<\kappa $
.
Proof Suppose not, and let
![]() $\alpha $
be the least counterexample. As
$\alpha $
be the least counterexample. As
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\chi $
-inaccessible,
${<}\chi $
-inaccessible,
![]() $\operatorname {\mathrm {cf}}(\alpha )\ge \chi $
. By minimality of
$\operatorname {\mathrm {cf}}(\alpha )\ge \chi $
. By minimality of
![]() $\alpha $
,
$\alpha $
,
As
![]() $\kappa $
is in particular
$\kappa $
is in particular
![]() ${<}\theta $
-inaccessible, moreover
${<}\theta $
-inaccessible, moreover
It follows that we may fix
![]() $B\in [\kappa \setminus (\alpha +1)]^{\kappa }$
and
$B\in [\kappa \setminus (\alpha +1)]^{\kappa }$
and
![]() $i<\theta $
such that:
$i<\theta $
such that:
-
• for every
 $\beta \in B$
,
$\beta \in B$
,
 $i(\beta )\le i$
;
$i(\beta )\le i$
; -
•
 $\beta \mapsto C^i_{\beta }\cap \alpha $
is an injection from B to the family of cofinal subsets of
$\beta \mapsto C^i_{\beta }\cap \alpha $
is an injection from B to the family of cofinal subsets of
 $\alpha $
.
$\alpha $
.
Consequently,
![]() $\beta \mapsto D^c_{\le i}(\beta )\cap \alpha $
is an injection from B to the family of cofinal subsets of
$\beta \mapsto D^c_{\le i}(\beta )\cap \alpha $
is an injection from B to the family of cofinal subsets of
![]() $\alpha $
. Now, as
$\alpha $
. Now, as
![]() $\operatorname {\mathrm {cf}}(\alpha )\ge \chi $
and c is
$\operatorname {\mathrm {cf}}(\alpha )\ge \chi $
and c is
![]() $E^{\kappa }_{\ge \chi }$
-closed, it follows that for every
$E^{\kappa }_{\ge \chi }$
-closed, it follows that for every
![]() $\beta \in B$
,
$\beta \in B$
,
![]() $c(\alpha ,\beta )\le i$
. But, then, by subadditivity, for every
$c(\alpha ,\beta )\le i$
. But, then, by subadditivity, for every
![]() $\beta \in B$
,
$\beta \in B$
,
![]() $D^c_{\le i}(\beta )\cap \alpha =D^c_{\le i}(\alpha )$
. This is a contradiction.
$D^c_{\le i}(\beta )\cap \alpha =D^c_{\le i}(\alpha )$
. This is a contradiction.
For each
![]() $i<\theta $
, let
$i<\theta $
, let
![]() $\rho _2^i:[\kappa ]^2\rightarrow \omega $
be the corresponding number of steps function derived from walking along
$\rho _2^i:[\kappa ]^2\rightarrow \omega $
be the corresponding number of steps function derived from walking along
![]() $\vec C^i$
, as in [Reference Todorcevic34, Section 6.3]. Then, for all
$\vec C^i$
, as in [Reference Todorcevic34, Section 6.3]. Then, for all
![]() $i<\theta $
and
$i<\theta $
and
![]() $\beta <\kappa $
, define a function
$\beta <\kappa $
, define a function
![]() $\rho _{2\beta }^i:\beta \rightarrow \omega $
via
$\rho _{2\beta }^i:\beta \rightarrow \omega $
via
![]() $\rho _{2\beta }^i(\alpha ):=\rho _2^i(\alpha ,\beta )$
. Finally, let
$\rho _{2\beta }^i(\alpha ):=\rho _2^i(\alpha ,\beta )$
. Finally, let
By Claim 3.10.1,
![]() $\mathcal T:=(T,{\subseteq })$
is a
$\mathcal T:=(T,{\subseteq })$
is a
![]() $\kappa $
-tree.
$\kappa $
-tree.
Claim 3.10.2.
![]() $\mathcal T$
has no branch of size
$\mathcal T$
has no branch of size
![]() $\kappa $
.
$\kappa $
.
Proof Otherwise, by a standard argument (e.g., the proof of [Reference Rinot28, Corollary 2.6]), there exists
![]() $i<\theta $
for which
$i<\theta $
for which
![]() $\rho _2^i$
admits a homogeneous set of size
$\rho _2^i$
admits a homogeneous set of size
![]() $\kappa $
. Fix such an i. By [Reference Todorcevic34, Theorem 6.3.2], then, we may fix a club
$\kappa $
. Fix such an i. By [Reference Todorcevic34, Theorem 6.3.2], then, we may fix a club
![]() $C\subseteq \kappa $
such that, for every
$C\subseteq \kappa $
such that, for every
![]() $\alpha <\kappa $
, there exists
$\alpha <\kappa $
, there exists
![]() $\beta <\kappa $
such that
$\beta <\kappa $
such that
![]() $C\cap \alpha \subseteq C^i_{\beta }$
. By the definition of
$C\cap \alpha \subseteq C^i_{\beta }$
. By the definition of
![]() $\vec C^i$
, for every
$\vec C^i$
, for every
![]() $\alpha <\kappa $
with
$\alpha <\kappa $
with
![]() $\operatorname {\mathrm {otp}}(C\cap \alpha )>\theta $
, it follows that there exist
$\operatorname {\mathrm {otp}}(C\cap \alpha )>\theta $
, it follows that there exist
![]() $j<\theta $
and
$j<\theta $
and
![]() $\beta <\kappa $
such that
$\beta <\kappa $
such that
![]() $C\cap \alpha \subseteq \operatorname {\mathrm {cl}}(D^c_{\le j}(\beta ))$
. By the pigeonhole principle, we may now fix
$C\cap \alpha \subseteq \operatorname {\mathrm {cl}}(D^c_{\le j}(\beta ))$
. By the pigeonhole principle, we may now fix
![]() $j<\kappa $
such that for every
$j<\kappa $
such that for every
![]() $\alpha <\kappa $
, there exists
$\alpha <\kappa $
, there exists
![]() $\beta _{\alpha }\ge \alpha $
such that
$\beta _{\alpha }\ge \alpha $
such that
![]() $C\cap \alpha \subseteq \operatorname {\mathrm {cl}}(D^c_{\le j}(\beta _{\alpha }))$
.
$C\cap \alpha \subseteq \operatorname {\mathrm {cl}}(D^c_{\le j}(\beta _{\alpha }))$
.
As c in particular witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,3)$
, we may find
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,3)$
, we may find
![]() $(\gamma ,\alpha )\in [C\cap E^{\kappa }_{\ge \chi }]^2$
such that
$(\gamma ,\alpha )\in [C\cap E^{\kappa }_{\ge \chi }]^2$
such that
![]() $c(\gamma ,\beta _{\alpha })>j$
. As
$c(\gamma ,\beta _{\alpha })>j$
. As
![]() $\gamma \in C\cap \alpha $
, we infer that
$\gamma \in C\cap \alpha $
, we infer that
![]() $\gamma \in \operatorname {\mathrm {cl}}(D^c_{\le j}(\beta _{\alpha }))$
. As
$\gamma \in \operatorname {\mathrm {cl}}(D^c_{\le j}(\beta _{\alpha }))$
. As
![]() $\gamma \in E^{\kappa }_{\ge \chi }$
and c is
$\gamma \in E^{\kappa }_{\ge \chi }$
and c is
![]() $ E^{\kappa }_{\ge \chi }$
-closed, it follows that
$ E^{\kappa }_{\ge \chi }$
-closed, it follows that
![]() $\gamma \in D^c_{\le j}(\beta _{\alpha })$
, contradicting the fact
$\gamma \in D^c_{\le j}(\beta _{\alpha })$
, contradicting the fact
![]() $c(\gamma ,\beta _{\alpha })>j$
.
$c(\gamma ,\beta _{\alpha })>j$
.
Claim 3.10.3.
![]() ${\mathcal T}$
admits a
${\mathcal T}$
admits a
![]() $\theta $
-ascent path.
$\theta $
-ascent path.
Proof As
![]() $\kappa \ge \aleph _2$
,
$\kappa \ge \aleph _2$
,
![]() $S:=\operatorname {\mathrm {acc}}(\kappa )\setminus E^{\kappa }_{\theta }$
is stationary. For every
$S:=\operatorname {\mathrm {acc}}(\kappa )\setminus E^{\kappa }_{\theta }$
is stationary. For every
![]() $\alpha <\kappa $
, define
$\alpha <\kappa $
, define
![]() $f_{\alpha }:\theta \rightarrow T_{\alpha }$
via
$f_{\alpha }:\theta \rightarrow T_{\alpha }$
via
![]() $f_{\alpha }(i):=\rho _{2\min (S\setminus \alpha )}^i\mathbin \upharpoonright \alpha $
. To see that
$f_{\alpha }(i):=\rho _{2\min (S\setminus \alpha )}^i\mathbin \upharpoonright \alpha $
. To see that
![]() $\langle f_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
forms a
$\langle f_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
forms a
![]() $\theta $
-ascent path through our tree, fix arbitrary
$\theta $
-ascent path through our tree, fix arbitrary
![]() $\alpha <\beta <\kappa $
. Write
$\alpha <\beta <\kappa $
. Write
![]() $\gamma :=\min (S\setminus \alpha )$
and
$\gamma :=\min (S\setminus \alpha )$
and
![]() ${\delta :=\min (S\setminus \beta )}$
. To avoid trivialities, suppose that
${\delta :=\min (S\setminus \beta )}$
. To avoid trivialities, suppose that
![]() $\gamma \neq \delta $
, so that
$\gamma \neq \delta $
, so that
![]() $\alpha \le \gamma <\beta \le \delta $
. As
$\alpha \le \gamma <\beta \le \delta $
. As
![]() $(\gamma ,\delta )\in [S]^2$
,
$(\gamma ,\delta )\in [S]^2$
,
![]() $i:=\max \{i(\gamma ),i(\delta ),c(\gamma ,\delta )\}$
is
$i:=\max \{i(\gamma ),i(\delta ),c(\gamma ,\delta )\}$
is
![]() $<\theta $
, and, for all
$<\theta $
, and, for all
![]() $j\in [i,\theta )$
,
$j\in [i,\theta )$
,
![]() $C_{\gamma }^j:=\operatorname {\mathrm {cl}}(D^c_{\le j}(\gamma ))$
and
$C_{\gamma }^j:=\operatorname {\mathrm {cl}}(D^c_{\le j}(\gamma ))$
and
![]() $C_{\delta }^j:=\operatorname {\mathrm {cl}}(D^c_{\le j}(\delta ))$
. By subadditivity, for every
$C_{\delta }^j:=\operatorname {\mathrm {cl}}(D^c_{\le j}(\delta ))$
. By subadditivity, for every
![]() $\epsilon <\gamma $
,
$\epsilon <\gamma $
,
![]() $c(\epsilon ,\gamma )\le \max \{c(\epsilon ,\delta ),c(\gamma ,\delta )\}$
and
$c(\epsilon ,\gamma )\le \max \{c(\epsilon ,\delta ),c(\gamma ,\delta )\}$
and
![]() $c(\epsilon ,\delta )\le \max \{c(\epsilon ,\gamma ),c(\gamma ,\delta )\}$
. So, for every
$c(\epsilon ,\delta )\le \max \{c(\epsilon ,\gamma ),c(\gamma ,\delta )\}$
. So, for every
![]() $j\in [i,\theta )$
, from
$j\in [i,\theta )$
, from
![]() $c(\gamma ,\delta )\le i\le j$
, we infer that
$c(\gamma ,\delta )\le i\le j$
, we infer that
![]() $C^j_{\gamma }=C^j_{\delta }\cap \gamma $
,
$C^j_{\gamma }=C^j_{\delta }\cap \gamma $
,
![]() $\rho _{2\gamma }^j=\rho _{2\delta }^j$
, and
$\rho _{2\gamma }^j=\rho _{2\delta }^j$
, and
![]() $f_{\alpha }(j)\subseteq f_{\beta }(j)$
, as sought.
$f_{\alpha }(j)\subseteq f_{\beta }(j)$
, as sought.
This completes the proof.
3.2 Locally small colorings
Definition 3.11. A coloring
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
is locally small iff
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
is locally small iff
![]() $|D^c_{\le i}(\beta )|<\lambda $
for all
$|D^c_{\le i}(\beta )|<\lambda $
for all
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
and
$i<\operatorname {\mathrm {cf}}(\lambda )$
and
![]() $\beta <\lambda ^+$
.
$\beta <\lambda ^+$
.
By Corollary 3.27, if
![]() $\lambda $
is regular, then any locally small coloring is a witness to
$\lambda $
is regular, then any locally small coloring is a witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\lambda ,\lambda )$
. In the general case, a locally small coloring witnesses an unbalanced strengthening of
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\lambda ,\lambda )$
. In the general case, a locally small coloring witnesses an unbalanced strengthening of
![]() $\operatorname {\mathrm {U}}(\lambda ^+,2,\operatorname {\mathrm {cf}}(\lambda ),\operatorname {\mathrm {cf}}(\lambda ))$
, as follows.
$\operatorname {\mathrm {U}}(\lambda ^+,2,\operatorname {\mathrm {cf}}(\lambda ),\operatorname {\mathrm {cf}}(\lambda ))$
, as follows.
Lemma 3.12. Suppose that
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
is a locally small coloring.
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
is a locally small coloring.
-
(1) For every
 $\nu <\operatorname {\mathrm {cf}}(\lambda )$
, c witnesses
$\nu <\operatorname {\mathrm {cf}}(\lambda )$
, c witnesses
 $\operatorname {\mathrm {U}}(\lambda ^+,\lambda \circledast \nu ,\operatorname {\mathrm {cf}}(\lambda ),\operatorname {\mathrm {cf}}(\lambda ))$
.
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda \circledast \nu ,\operatorname {\mathrm {cf}}(\lambda ),\operatorname {\mathrm {cf}}(\lambda ))$
. -
(2) If c is subadditive, then c moreover witnesses
 $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),\operatorname {\mathrm {cf}}(\lambda ))$
.
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),\operatorname {\mathrm {cf}}(\lambda ))$
.
Proof (1) Suppose that we are given
![]() $\sigma < \operatorname {\mathrm {cf}}(\lambda )$
, a pairwise disjoint subfamily
$\sigma < \operatorname {\mathrm {cf}}(\lambda )$
, a pairwise disjoint subfamily
![]() $\mathcal {A} \subseteq [\lambda ^+]^{\sigma }$
of size
$\mathcal {A} \subseteq [\lambda ^+]^{\sigma }$
of size
![]() $\lambda ^+$
, and some
$\lambda ^+$
, and some
![]() $i < \operatorname {\mathrm {cf}}(\lambda )$
. Find a large enough
$i < \operatorname {\mathrm {cf}}(\lambda )$
. Find a large enough
![]() $\epsilon <\lambda ^+$
such that
$\epsilon <\lambda ^+$
such that
![]() $\mathcal A\cap \mathcal P(\epsilon )$
has size
$\mathcal A\cap \mathcal P(\epsilon )$
has size
![]() $\lambda $
. Now, given
$\lambda $
. Now, given
![]() $\nu <\operatorname {\mathrm {cf}}(\lambda )$
, fix any
$\nu <\operatorname {\mathrm {cf}}(\lambda )$
, fix any
![]() $\mathcal B'\in [\mathcal A]^{\nu }$
with
$\mathcal B'\in [\mathcal A]^{\nu }$
with
![]() $\min (\bigcup \mathcal B')>\epsilon $
. Since c is locally small and
$\min (\bigcup \mathcal B')>\epsilon $
. Since c is locally small and
![]() $|\bigcup \mathcal B'|<\operatorname {\mathrm {cf}}(\lambda )$
,
$|\bigcup \mathcal B'|<\operatorname {\mathrm {cf}}(\lambda )$
,
![]() $X:=\bigcup _{b\in \mathcal B'}\bigcup _{\beta \in b} D^c_{\le i}(\beta )$
has size
$X:=\bigcup _{b\in \mathcal B'}\bigcup _{\beta \in b} D^c_{\le i}(\beta )$
has size
![]() $< \lambda $
. As
$< \lambda $
. As
![]() $\mathcal A\cap \mathcal P(\epsilon )$
consists of
$\mathcal A\cap \mathcal P(\epsilon )$
consists of
![]() $\lambda $
-many pairwise disjoint sets, it follows that
$\lambda $
-many pairwise disjoint sets, it follows that
![]() $\mathcal A':=\{ a\in \mathcal A\cap \mathcal P(\epsilon )\mathrel {|} a\cap X=\emptyset \}$
has size
$\mathcal A':=\{ a\in \mathcal A\cap \mathcal P(\epsilon )\mathrel {|} a\cap X=\emptyset \}$
has size
![]() $\lambda $
. Evidently, for every
$\lambda $
. Evidently, for every
![]() $(a,b)\in \mathcal A'\times \mathcal B'$
, we have
$(a,b)\in \mathcal A'\times \mathcal B'$
, we have
![]() $a<b$
and
$a<b$
and
![]() $\min (c[a \times b])> i$
.
$\min (c[a \times b])> i$
.
(2) Suppose that c is subadditive. By Lemma 3.2(2), it suffices to prove that c witnesses
![]() $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),2)$
. So, let
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),2)$
. So, let
![]() $A\in [\lambda ^+]^{\lambda ^+}$
and
$A\in [\lambda ^+]^{\lambda ^+}$
and
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
be given; we need to find
$i<\operatorname {\mathrm {cf}}(\lambda )$
be given; we need to find
![]() $B\in [A]^{\lambda ^+}$
such that
$B\in [A]^{\lambda ^+}$
such that
![]() $c(\alpha ,\beta )>i$
for all
$c(\alpha ,\beta )>i$
for all
![]() $(\alpha ,\beta )\in [B]^{\lambda ^+}$
.
$(\alpha ,\beta )\in [B]^{\lambda ^+}$
.
As in the proof of Lemma 3.2, we define a tree ordering
![]() $<_i$
on
$<_i$
on
![]() $\lambda ^+$
by letting
$\lambda ^+$
by letting
![]() $\alpha <_i\beta $
iff
$\alpha <_i\beta $
iff
![]() $\alpha <\beta $
and
$\alpha <\beta $
and
![]() $c(\alpha ,\beta )\le i$
. By Clause (1), c in particular witnesses
$c(\alpha ,\beta )\le i$
. By Clause (1), c in particular witnesses
![]() $\operatorname {\mathrm {U}}(\lambda ^+,2,\operatorname {\mathrm {cf}}(\lambda ),2)$
, and hence
$\operatorname {\mathrm {U}}(\lambda ^+,2,\operatorname {\mathrm {cf}}(\lambda ),2)$
, and hence
![]() $(\lambda ^+,<_i)$
admits no chains of size
$(\lambda ^+,<_i)$
admits no chains of size
![]() $\lambda ^+$
. Assuming that the sought-after
$\lambda ^+$
. Assuming that the sought-after
![]() $B\in [A]^{\lambda ^+}$
does not exist, it follows that
$B\in [A]^{\lambda ^+}$
does not exist, it follows that
![]() $(A,<_i)$
has no antichains of size
$(A,<_i)$
has no antichains of size
![]() $\lambda ^+$
, so
$\lambda ^+$
, so
![]() $(A,<_i)$
is a
$(A,<_i)$
is a
![]() $\lambda ^+$
-Souslin tree. Forcing with this tree, we arrive at a
$\lambda ^+$
-Souslin tree. Forcing with this tree, we arrive at a
![]() $\lambda ^+$
-distributive forcing extension
$\lambda ^+$
-distributive forcing extension
![]() $V[G]$
in which
$V[G]$
in which
![]() $(A,<_i)$
does admit a chain of size
$(A,<_i)$
does admit a chain of size
![]() $\lambda ^+$
. But
$\lambda ^+$
. But
![]() $V[G]$
is a
$V[G]$
is a
![]() $\lambda ^+$
-distributive forcing extension of V, and hence c remains locally small in
$\lambda ^+$
-distributive forcing extension of V, and hence c remains locally small in
![]() $V[G]$
, and in particular, it still witnesses
$V[G]$
, and in particular, it still witnesses
![]() $\operatorname {\mathrm {U}}(\lambda ^+,2,\operatorname {\mathrm {cf}}(\lambda ),2)$
. This is a contradiction.
$\operatorname {\mathrm {U}}(\lambda ^+,2,\operatorname {\mathrm {cf}}(\lambda ),2)$
. This is a contradiction.
Lemma 3.13. For every infinite cardinal
![]() $\lambda $
, there exists a locally small witness to
$\lambda $
, there exists a locally small witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),\lambda )$
which is subadditive of the first kind.
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),\lambda )$
which is subadditive of the first kind.
Proof We focus on the case in which
![]() $\lambda $
is singular, since, if
$\lambda $
is singular, since, if
![]() $\lambda $
is regular, a better result is given by Lemma 3.14(1). Let
$\lambda $
is regular, a better result is given by Lemma 3.14(1). Let
![]() $\langle \lambda _i\mathrel {|} i<\operatorname {\mathrm {cf}}(\lambda )\rangle $
be a strictly increasing sequence of regular uncountable cardinals converging to
$\langle \lambda _i\mathrel {|} i<\operatorname {\mathrm {cf}}(\lambda )\rangle $
be a strictly increasing sequence of regular uncountable cardinals converging to
![]() $\lambda $
. By [Reference Shelah30, Lemma 4.1], there exists a coloring
$\lambda $
. By [Reference Shelah30, Lemma 4.1], there exists a coloring
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
which is subadditive of the first kind and locally small in the following strong sense: for all
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
which is subadditive of the first kind and locally small in the following strong sense: for all
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
and
$i<\operatorname {\mathrm {cf}}(\lambda )$
and
![]() $\beta <\lambda ^+$
,
$\beta <\lambda ^+$
,
![]() $|D^c_{\le i}(\beta )|\le \lambda _i$
.
$|D^c_{\le i}(\beta )|\le \lambda _i$
.
Claim 3.13.1. For every pairwise disjoint subfamily
![]() $\mathcal A\subseteq [\lambda ^+]^{<\lambda }$
of size
$\mathcal A\subseteq [\lambda ^+]^{<\lambda }$
of size
![]() $\lambda ^+$
, for every club
$\lambda ^+$
, for every club
![]() $D\subseteq \lambda ^+$
, and for every
$D\subseteq \lambda ^+$
, and for every
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
, there exist
$i<\operatorname {\mathrm {cf}}(\lambda )$
, there exist
![]() $\gamma \in D$
,
$\gamma \in D$
,
![]() $a\in \mathcal A$
, and
$a\in \mathcal A$
, and
![]() $\epsilon < \gamma $
such that:
$\epsilon < \gamma $
such that:
-
•
 $\gamma < a$
;
$\gamma < a$
; -
• for all
 $\alpha \in (\epsilon , \gamma )$
and
$\alpha \in (\epsilon , \gamma )$
and
 $\beta \in a$
, we have
$\beta \in a$
, we have
 $c(\alpha ,\beta )>i$
.
$c(\alpha ,\beta )>i$
.
Proof Given
![]() $\mathcal A$
and i as above, fix a large enough
$\mathcal A$
and i as above, fix a large enough
![]() $j<\operatorname {\mathrm {cf}}(\lambda )$
such that
$j<\operatorname {\mathrm {cf}}(\lambda )$
such that
![]() $j\ge i$
and
$j\ge i$
and
![]() $\mathcal A_j:=\{ a\in \mathcal A\mathrel {|} |a|\le \lambda _j\}$
has size
$\mathcal A_j:=\{ a\in \mathcal A\mathrel {|} |a|\le \lambda _j\}$
has size
![]() $\lambda ^+$
. Now, given a club
$\lambda ^+$
. Now, given a club
![]() $D\subseteq \lambda ^+$
, fix
$D\subseteq \lambda ^+$
, fix
![]() $\gamma \in D\cap E^{\lambda ^+}_{>\lambda _j}$
, and pick any
$\gamma \in D\cap E^{\lambda ^+}_{>\lambda _j}$
, and pick any
![]() $a\in \mathcal A_j$
with
$a\in \mathcal A_j$
with
![]() $\gamma <a$
.
$\gamma <a$
.
For all
![]() $\beta \in a$
, we have
$\beta \in a$
, we have
![]() $|D^c_{\le j}(\beta )|\le \lambda _j<\operatorname {\mathrm {cf}}(\gamma )$
, so
$|D^c_{\le j}(\beta )|\le \lambda _j<\operatorname {\mathrm {cf}}(\gamma )$
, so
![]() $\epsilon :=\sup (\bigcup \{D^c_{\le j}(\beta )\cap \gamma \mathrel {|} \beta \in a\})$
is
$\epsilon :=\sup (\bigcup \{D^c_{\le j}(\beta )\cap \gamma \mathrel {|} \beta \in a\})$
is
![]() $<\gamma $
. Then for all
$<\gamma $
. Then for all
![]() $\alpha \in (\epsilon ,\gamma )$
and
$\alpha \in (\epsilon ,\gamma )$
and
![]() $\beta \in a$
, we have
$\beta \in a$
, we have
![]() $c(\alpha ,\beta )>j\ge i$
.
$c(\alpha ,\beta )>j\ge i$
.
It now follows from Fact 2.2 that c witnesses
![]() $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),\lambda )$
.
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),\lambda )$
.
Lemma 3.14 (Todorcevic [Reference Todorcevic34]).
-
(1) If
 $\lambda $
is regular, then there exists a locally small and subadditive witness to
$\lambda $
is regular, then there exists a locally small and subadditive witness to
 $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+, \lambda ,\lambda )$
.
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+, \lambda ,\lambda )$
. -
(2) If
 $\square _{\lambda }$
holds, then there exists a locally small and subadditive witness to
$\square _{\lambda }$
holds, then there exists a locally small and subadditive witness to
 $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),\lambda )$
which is moreover closed.
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ),\lambda )$
which is moreover closed.
Proof
-
(1) Consider the function
 $\rho :[\lambda ^+]^2\rightarrow \lambda $
defined in [Reference Todorcevic34, Section 9.1]. By [Reference Todorcevic34, Lemma 9.1.1],
$\rho :[\lambda ^+]^2\rightarrow \lambda $
defined in [Reference Todorcevic34, Section 9.1]. By [Reference Todorcevic34, Lemma 9.1.1],
 $\rho $
is locally small. By [Reference Todorcevic34, Lemma 9.1.2],
$\rho $
is locally small. By [Reference Todorcevic34, Lemma 9.1.2],
 $\rho $
is subadditive. By [Reference Todorcevic34, Theorem 6.2.7],
$\rho $
is subadditive. By [Reference Todorcevic34, Theorem 6.2.7],
 $\rho $
is a witness to
$\rho $
is a witness to
 $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\lambda ,\lambda )$
.
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\lambda ,\lambda )$
. -
(2) This follows from Lemmas 7.3.7, 7.3.8, 7.3.11, and 7.3.12 of [Reference Todorcevic34], together with Lemma 3.2(3). For
 $\lambda $
singular, a slightly better result is proved in [Reference Lambie-Hanson16, Theorem 5.8].
$\lambda $
singular, a slightly better result is proved in [Reference Lambie-Hanson16, Theorem 5.8].
The following result, due independently to Shani and Lambie-Hanson, shows that the hypothesis of
![]() $\square _{\lambda }$
cannot be weakened to
$\square _{\lambda }$
cannot be weakened to
![]() $\square _{\lambda , 2}$
in Lemma 3.14(2). (We note that
$\square _{\lambda , 2}$
in Lemma 3.14(2). (We note that
![]() $\textsf{GCH}$
is not explicitly mentioned in the quoted results, but it is evident from their proofs that, if
$\textsf{GCH}$
is not explicitly mentioned in the quoted results, but it is evident from their proofs that, if
![]() $\textsf{GCH}$
holds in the relevant ground models, then it continues to hold in the forcing extensions witnessing the conclusion of the result.)
$\textsf{GCH}$
holds in the relevant ground models, then it continues to hold in the forcing extensions witnessing the conclusion of the result.)
Fact 3.15 (Shani [Reference Shani29, Theorem 1] and Lambie-Hanson [Reference Lambie-Hanson16, Corollaries 5.13 and 5.14]).
Relative to the existence of large cardinals, it is consistent with
![]() $\textsf{GCH}$
that there is an uncountable cardinal
$\textsf{GCH}$
that there is an uncountable cardinal
![]() $\lambda $
such that
$\lambda $
such that
![]() $\square _{\lambda , 2}$
holds, and, for every
$\square _{\lambda , 2}$
holds, and, for every
![]() $\theta < \lambda $
,
$\theta < \lambda $
,
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, 2, \theta , 2)$
fails.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, 2, \theta , 2)$
fails.
![]() $\lambda $
can be either regular or singular here, though attaining the result for singular
$\lambda $
can be either regular or singular here, though attaining the result for singular
![]() $\lambda $
requires significantly larger cardinals than attaining it for regular
$\lambda $
requires significantly larger cardinals than attaining it for regular
![]() $\lambda $
.
$\lambda $
.
The principle
![]() $\operatorname {\mathrm {SAP}}^*_{\lambda }$
was introduced in [Reference Rinot27, Definition 2.12] as a weakening of Jensen’s weak square principle
$\operatorname {\mathrm {SAP}}^*_{\lambda }$
was introduced in [Reference Rinot27, Definition 2.12] as a weakening of Jensen’s weak square principle
![]() $\square ^*_{\lambda }$
. By [Reference Rinot27, Theorem 2.6], assuming
$\square ^*_{\lambda }$
. By [Reference Rinot27, Theorem 2.6], assuming
![]() $2^{\lambda }=\lambda ^+$
,
$2^{\lambda }=\lambda ^+$
,
![]() $\operatorname {\mathrm {SAP}}^*_{\lambda }$
implies that
$\operatorname {\mathrm {SAP}}^*_{\lambda }$
implies that
![]() holds for every stationary subset
holds for every stationary subset
![]() $S\subseteq \lambda ^+$
that reflects stationarily often. By [Reference Rinot27, Corollary 2.16], if
$S\subseteq \lambda ^+$
that reflects stationarily often. By [Reference Rinot27, Corollary 2.16], if
![]() $\lambda $
is a singular cardinal such that
$\lambda $
is a singular cardinal such that
![]() $2^{<\lambda }<2^{\lambda }=\lambda ^+$
and every stationary subset of
$2^{<\lambda }<2^{\lambda }=\lambda ^+$
and every stationary subset of
![]() $E^{\lambda ^+}_{\operatorname {\mathrm {cf}}(\lambda )}$
reflects, then
$E^{\lambda ^+}_{\operatorname {\mathrm {cf}}(\lambda )}$
reflects, then
![]() $\operatorname {\mathrm {SAP}}^*_{\lambda }$
moreover implies
$\operatorname {\mathrm {SAP}}^*_{\lambda }$
moreover implies
![]() .
.
Proposition 3.16. Suppose that
![]() $\lambda $
is a singular cardinal and there exists a locally small and subadditive coloring
$\lambda $
is a singular cardinal and there exists a locally small and subadditive coloring
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
. Then
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
. Then
![]() $\operatorname {\mathrm {SAP}}^*_{\lambda }$
holds and
$\operatorname {\mathrm {SAP}}^*_{\lambda }$
holds and
![]() $E^{\lambda ^+}_{>\operatorname {\mathrm {cf}}(\lambda )}\in I[\lambda ^+;\lambda ]$
.
$E^{\lambda ^+}_{>\operatorname {\mathrm {cf}}(\lambda )}\in I[\lambda ^+;\lambda ]$
.
Proof Let c be as above. By [Reference Rinot27, Definitions 2.4 and 2.12], as c is locally small and subadditive of the first kind,Footnote
2
to verify
![]() $\operatorname {\mathrm {SAP}}^*_{\lambda }$
, it suffices to verify that for every stationary
$\operatorname {\mathrm {SAP}}^*_{\lambda }$
, it suffices to verify that for every stationary
![]() $S\subseteq E^{\lambda ^+}_{\operatorname {\mathrm {cf}}(\lambda )}$
and every
$S\subseteq E^{\lambda ^+}_{\operatorname {\mathrm {cf}}(\lambda )}$
and every
![]() $\gamma \in \operatorname {\mathrm {Tr}}(S)$
, there exists a stationary
$\gamma \in \operatorname {\mathrm {Tr}}(S)$
, there exists a stationary
![]() $S_{\gamma }\subseteq S\cap \gamma $
such that
$S_{\gamma }\subseteq S\cap \gamma $
such that
![]() $\sup (c"[S_{\gamma }]^2)<\operatorname {\mathrm {cf}}(\lambda )$
.
$\sup (c"[S_{\gamma }]^2)<\operatorname {\mathrm {cf}}(\lambda )$
.
To this end, fix arbitrary
![]() $\gamma \in E^{\lambda ^+}_{>\operatorname {\mathrm {cf}}(\lambda )}$
and a stationary
$\gamma \in E^{\lambda ^+}_{>\operatorname {\mathrm {cf}}(\lambda )}$
and a stationary
![]() $s\subseteq \gamma $
. As
$s\subseteq \gamma $
. As
![]() $\operatorname {\mathrm {cf}}(\gamma )>\operatorname {\mathrm {cf}}(\lambda )$
, there exists a large enough
$\operatorname {\mathrm {cf}}(\gamma )>\operatorname {\mathrm {cf}}(\lambda )$
, there exists a large enough
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
such that
$i<\operatorname {\mathrm {cf}}(\lambda )$
such that
![]() $S_{\gamma }:=D^c_{\le i}(\gamma )\cap s$
is stationary in
$S_{\gamma }:=D^c_{\le i}(\gamma )\cap s$
is stationary in
![]() $\gamma $
. Since c is subadditive of the second kind, for any pair
$\gamma $
. Since c is subadditive of the second kind, for any pair
![]() $(\alpha ,\beta )\in [S_{\gamma }]^2$
, we have that
$(\alpha ,\beta )\in [S_{\gamma }]^2$
, we have that
![]() $c(\alpha ,\beta )\le \max \{c(\alpha ,\gamma ),c(\beta ,\gamma )\}\le i$
. Therefore,
$c(\alpha ,\beta )\le \max \{c(\alpha ,\gamma ),c(\beta ,\gamma )\}\le i$
. Therefore,
![]() $\sup (c"[S_{\gamma }]^2)\le i$
. Recalling [Reference Rinot27, Definition 2.3], the very same argument shows that
$\sup (c"[S_{\gamma }]^2)\le i$
. Recalling [Reference Rinot27, Definition 2.3], the very same argument shows that
![]() $E^{\lambda ^+}_{>\operatorname {\mathrm {cf}}(\lambda )}\in I[\lambda ^+;\lambda ]$
.
$E^{\lambda ^+}_{>\operatorname {\mathrm {cf}}(\lambda )}\in I[\lambda ^+;\lambda ]$
.
Corollary 3.17. If
![]() $\lambda $
is a singular strong limit and there exists a locally small and subadditive coloring
$\lambda $
is a singular strong limit and there exists a locally small and subadditive coloring
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
, then
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
, then
![]() $\operatorname {\mathrm {AP}}_{\lambda }$
holds.
$\operatorname {\mathrm {AP}}_{\lambda }$
holds.
Proof By the preceding proposition, the hypothesis implies that
![]() $E^{\lambda ^+}_{>\operatorname {\mathrm {cf}}(\lambda )}\in I[\lambda ^+;\lambda ]$
. Now, given that
$E^{\lambda ^+}_{>\operatorname {\mathrm {cf}}(\lambda )}\in I[\lambda ^+;\lambda ]$
. Now, given that
![]() $\lambda $
is a strong limit, we moreover get that
$\lambda $
is a strong limit, we moreover get that
![]() $\lambda ^+\in I[\lambda ^+;\lambda ]=I[\lambda ^+]$
, meaning that
$\lambda ^+\in I[\lambda ^+;\lambda ]=I[\lambda ^+]$
, meaning that
![]() $\operatorname {\mathrm {AP}}_{\lambda }$
holds.
$\operatorname {\mathrm {AP}}_{\lambda }$
holds.
3.3 Forms of coherence and levels of divergence
We will also be interested in variants of subadditivity, as captured by the next definition and by Definition 3.24.
Definition 3.18. A coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
is weakly subadditive iff the following two statements hold:
$c:[\kappa ]^2\rightarrow \theta $
is weakly subadditive iff the following two statements hold:
-
(1) c is weakly subadditive of the first kind, that is, for all
 $\beta < \gamma < \kappa $
and
$\beta < \gamma < \kappa $
and
 $i<\theta $
, there is
$i<\theta $
, there is
 $j<\theta $
such that
$j<\theta $
such that
 $D^c_{\le i}(\beta )\subseteq D^c_{\le j}(\gamma )$
.
$D^c_{\le i}(\beta )\subseteq D^c_{\le j}(\gamma )$
. -
(2) c is weakly subadditive of the second kind, that is, for all
 $\beta < \gamma < \kappa $
and
$\beta < \gamma < \kappa $
and
 $i<\theta $
, there is
$i<\theta $
, there is
 $j<\theta $
such that
$j<\theta $
such that
 $D^c_{\le i}(\gamma )\cap \beta \subseteq D^c_{\le j}(\beta )$
.
$D^c_{\le i}(\gamma )\cap \beta \subseteq D^c_{\le j}(\beta )$
.
Remark 3.19. The statement of [Reference Lambie-Hanson16, Lemma 5.11], together with Fact 3.15, makes it clear that it is consistent with
![]() $\textsf{GCH}+\square _{\lambda , 2}$
(for either a regular or a singular cardinal
$\textsf{GCH}+\square _{\lambda , 2}$
(for either a regular or a singular cardinal
![]() $\lambda $
), that, for every
$\lambda $
), that, for every
![]() $\theta < \lambda $
, there exists no witness to
$\theta < \lambda $
, there exists no witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+, 2, \theta , 2)$
which is weakly subadditive of the first kind. In particular, very good scales for
$\operatorname {\mathrm {U}}(\lambda ^+, 2, \theta , 2)$
which is weakly subadditive of the first kind. In particular, very good scales for
![]() $\aleph _{\omega }$
, and hence also the weaker combinatorial principle
$\aleph _{\omega }$
, and hence also the weaker combinatorial principle
![]() $\operatorname {\mathrm {ADS}}_{\aleph _{\omega }}$
, both of which are consequences of
$\operatorname {\mathrm {ADS}}_{\aleph _{\omega }}$
, both of which are consequences of
![]() $\square _{\aleph _{\omega }, 2}$
, are not sufficient to get a weakly subadditive witness to
$\square _{\aleph _{\omega }, 2}$
, are not sufficient to get a weakly subadditive witness to
![]() $\operatorname {\mathrm {U}}(\aleph _{\omega +1}, 2, \aleph _n, 2)$
.
$\operatorname {\mathrm {U}}(\aleph _{\omega +1}, 2, \aleph _n, 2)$
.
Proposition 3.20. Suppose that
![]() $\chi \le \theta $
is a pair of infinite regular cardinals
$\chi \le \theta $
is a pair of infinite regular cardinals
![]() $<\kappa $
, and
$<\kappa $
, and
![]() $c:[\kappa ]^2\rightarrow \theta $
is a witness to
$c:[\kappa ]^2\rightarrow \theta $
is a witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
that is weakly subadditive of the second kind. If c is
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
that is weakly subadditive of the second kind. If c is
![]() $\Sigma $
-closed for some stationary
$\Sigma $
-closed for some stationary
![]() $\Sigma \subseteq E^{\kappa }_{\geq \chi }$
, then c witnesses
$\Sigma \subseteq E^{\kappa }_{\geq \chi }$
, then c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\chi )$
.
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\chi )$
.
Proof Let
![]() $\Sigma \subseteq E^{\kappa }_{\geq \chi }$
be stationary.
$\Sigma \subseteq E^{\kappa }_{\geq \chi }$
be stationary.
Claim 3.20.1. Suppose that
![]() $\mathcal A\subseteq [\kappa ]^{<\chi }$
is a family consisting of
$\mathcal A\subseteq [\kappa ]^{<\chi }$
is a family consisting of
![]() $\kappa $
-many pairwise disjoint sets, D is a club in
$\kappa $
-many pairwise disjoint sets, D is a club in
![]() $\kappa $
, and
$\kappa $
, and
![]() $i<\theta $
is a prescribed color. Then there exist
$i<\theta $
is a prescribed color. Then there exist
![]() $\gamma \in D \cap \Sigma $
and
$\gamma \in D \cap \Sigma $
and
![]() $a\in \mathcal A$
such that:
$a\in \mathcal A$
such that:
-
(a)
 $\gamma < a$
;
$\gamma < a$
; -
(b) for all
 $\beta \in a$
, we have
$\beta \in a$
, we have
 $c(\gamma ,\beta )>i$
.
$c(\gamma ,\beta )>i$
.
Proof For each
![]() $\delta <\kappa $
, pick
$\delta <\kappa $
, pick
![]() $a_{\delta }\in \mathcal A$
with
$a_{\delta }\in \mathcal A$
with
![]() $\delta < a_{\delta }$
. As
$\delta < a_{\delta }$
. As
![]() $\mathcal A\subseteq [\kappa ]^{<\operatorname {\mathrm {cf}}(\theta )}$
, we may define a function
$\mathcal A\subseteq [\kappa ]^{<\operatorname {\mathrm {cf}}(\theta )}$
, we may define a function
![]() $f:\kappa \rightarrow \theta $
via
$f:\kappa \rightarrow \theta $
via
Fix
![]() $j<\theta $
for which
$j<\theta $
for which
![]() $A:=\{ \delta \in D\cap \Sigma \mathrel {|} f(\delta )=j\}$
is cofinal. Since c witnesses
$A:=\{ \delta \in D\cap \Sigma \mathrel {|} f(\delta )=j\}$
is cofinal. Since c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, we can now pick
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, we can now pick
![]() $(\gamma ,\delta )\in [A]^2$
such that
$(\gamma ,\delta )\in [A]^2$
such that
![]() $c(\gamma ,\delta )>j$
. Clearly,
$c(\gamma ,\delta )>j$
. Clearly,
![]() $\gamma <a_{\delta }$
. Now, if there exists
$\gamma <a_{\delta }$
. Now, if there exists
![]() $\beta \in a_{\delta }$
such that
$\beta \in a_{\delta }$
such that
![]() $c(\gamma ,\beta )\le i$
, then
$c(\gamma ,\beta )\le i$
, then
![]() $\gamma \in D^c_{\le i}(\beta )\cap \delta \subseteq D^c_{\le j}(\delta )$
which is not the case. Therefore, both clauses of the claim hold for
$\gamma \in D^c_{\le i}(\beta )\cap \delta \subseteq D^c_{\le j}(\delta )$
which is not the case. Therefore, both clauses of the claim hold for
![]() $a:=a_{\delta }$
.
$a:=a_{\delta }$
.
Evidently, if c is
![]() $\Sigma $
-closed, then Clause (b) of the preceding is equivalent to:
$\Sigma $
-closed, then Clause (b) of the preceding is equivalent to:
-
(b’) there is
 $\epsilon < \gamma $
such that, for all
$\epsilon < \gamma $
such that, for all
 $\alpha \in (\epsilon , \gamma )$
and all
$\alpha \in (\epsilon , \gamma )$
and all
 $\beta \in a$
, we have
$\beta \in a$
, we have
 $c(\alpha ,\beta )>i$
.
$c(\alpha ,\beta )>i$
.
Thus, the implication
![]() $(2)\implies (3)$
of Fact 2.2 gives the desired conclusion.
$(2)\implies (3)$
of Fact 2.2 gives the desired conclusion.
Motivated by the proof of Lemma 3.10, we introduce the following definition.
Definition 3.21 (Levels of divergence).
For a coloring
![]() $c:[\kappa ]^2 \rightarrow \theta $
, let
$c:[\kappa ]^2 \rightarrow \theta $
, let
Note that
![]() $\partial (c)\subseteq E^{\kappa }_{\operatorname {\mathrm {cf}}(\theta )}$
and that c is vacuously
$\partial (c)\subseteq E^{\kappa }_{\operatorname {\mathrm {cf}}(\theta )}$
and that c is vacuously
![]() $\partial (c)$
-closed.
$\partial (c)$
-closed.
Lemma 3.22. Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
is a coloring. If c is weakly subadditive of the second kind, then
$c:[\kappa ]^2\rightarrow \theta $
is a coloring. If c is weakly subadditive of the second kind, then
Proof If c is weakly subadditive of the second kind, then for all
![]() $\beta <\gamma <\kappa $
and
$\beta <\gamma <\kappa $
and
![]() $i<\theta $
such that
$i<\theta $
such that
![]() $\sup (D^c_{\le i}(\gamma )\cap \beta )=\beta $
, there exists
$\sup (D^c_{\le i}(\gamma )\cap \beta )=\beta $
, there exists
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $D^c_{\le i}(\gamma )\cap \beta \subseteq D^c_{\le j}(\beta )$
, and hence
$D^c_{\le i}(\gamma )\cap \beta \subseteq D^c_{\le j}(\beta )$
, and hence
![]() $\sup (D^c_{\le j}(\beta ))=\beta $
.
$\sup (D^c_{\le j}(\beta ))=\beta $
.
We will be particularly interested in situations in which
![]() $\partial (c)$
is stationary in
$\partial (c)$
is stationary in
![]() $\kappa $
; one reason for this is the following lemma, indicating that colorings c for which
$\kappa $
; one reason for this is the following lemma, indicating that colorings c for which
![]() $\partial (c)$
is stationary automatically witness an instance of
$\partial (c)$
is stationary automatically witness an instance of
![]() $\operatorname {\mathrm {U}}(\ldots )$
.
$\operatorname {\mathrm {U}}(\ldots )$
.
Lemma 3.23. Suppose that
![]() $c:[\kappa ]^2 \rightarrow \theta $
is a coloring for which
$c:[\kappa ]^2 \rightarrow \theta $
is a coloring for which
![]() $\partial (c)$
is stationary. Then c witnesses
$\partial (c)$
is stationary. Then c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \operatorname {\mathrm {cf}}(\theta ))$
.
$\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \operatorname {\mathrm {cf}}(\theta ))$
.
Proof We prove that the coloring c satisfies Clause (2) of Fact 2.2 with
![]() $\chi := \operatorname {\mathrm {cf}}(\theta )$
, which will yield our desired conclusion. Fix a family
$\chi := \operatorname {\mathrm {cf}}(\theta )$
, which will yield our desired conclusion. Fix a family
![]() $\mathcal {A} \subseteq [\kappa ]^{<\operatorname {\mathrm {cf}}(\theta )}$
consisting of
$\mathcal {A} \subseteq [\kappa ]^{<\operatorname {\mathrm {cf}}(\theta )}$
consisting of
![]() $\kappa $
-many pairwise disjoint sets, a club
$\kappa $
-many pairwise disjoint sets, a club
![]() $D \subseteq \kappa $
, and an
$D \subseteq \kappa $
, and an
![]() $i < \theta $
. Since
$i < \theta $
. Since
![]() $\partial (c)$
is stationary, we can fix
$\partial (c)$
is stationary, we can fix
![]() $\gamma \in \partial (c) \cap D$
. Also fix an
$\gamma \in \partial (c) \cap D$
. Also fix an
![]() $a \in \mathcal {A}$
such that
$a \in \mathcal {A}$
such that
![]() $\gamma < a$
. As
$\gamma < a$
. As
![]() $\gamma \in \partial (c)$
, for all
$\gamma \in \partial (c)$
, for all
![]() $\beta \in a$
, we have
$\beta \in a$
, we have
![]() $\sup (D^c_{\leq i}(\beta ) \cap \gamma ) < \gamma $
. Since
$\sup (D^c_{\leq i}(\beta ) \cap \gamma ) < \gamma $
. Since
![]() $|a| < \operatorname {\mathrm {cf}}(\theta ) = \operatorname {\mathrm {cf}}(\gamma )$
, we can find
$|a| < \operatorname {\mathrm {cf}}(\theta ) = \operatorname {\mathrm {cf}}(\gamma )$
, we can find
![]() $\epsilon < \gamma $
such that
$\epsilon < \gamma $
such that
![]() $\sup (D^c_{\leq i}(\beta ) \cap \gamma ) < \epsilon $
for all
$\sup (D^c_{\leq i}(\beta ) \cap \gamma ) < \epsilon $
for all
![]() $\beta \in a$
. Now, for all
$\beta \in a$
. Now, for all
![]() $\alpha \in (\epsilon , \gamma )$
and all
$\alpha \in (\epsilon , \gamma )$
and all
![]() $\beta \in a$
, we have
$\beta \in a$
, we have
![]() $\alpha \notin D^c_{\leq i}(\beta )$
, so
$\alpha \notin D^c_{\leq i}(\beta )$
, so
![]() $c(\alpha , \beta )> i$
, as desired.
$c(\alpha , \beta )> i$
, as desired.
Definition 3.24 (Forms of coherence).
Let
![]() $c:[\kappa ]^2\rightarrow \theta $
be a coloring.
$c:[\kappa ]^2\rightarrow \theta $
be a coloring.
-
(1) c is
 $\ell _{\infty }$
-coherent iff for all
$\ell _{\infty }$
-coherent iff for all
 $\gamma <\delta <\kappa $
, there is
$\gamma <\delta <\kappa $
, there is
 $j<\theta $
such that, for all
$j<\theta $
such that, for all
 $i<\theta $
,
$i<\theta $
,
 $D^c_{\le i}(\gamma )\subseteq D^c_{\le i+j}(\delta )$
and
$D^c_{\le i}(\gamma )\subseteq D^c_{\le i+j}(\delta )$
and
 $D^c_{\le i}(\delta )\cap \gamma \subseteq D^c_{\le i+j}(\gamma )$
.
$D^c_{\le i}(\delta )\cap \gamma \subseteq D^c_{\le i+j}(\gamma )$
. -
(2) For a cardinal
 $\lambda <\kappa $
, c is
$\lambda <\kappa $
, c is
 $\lambda $
-coherent iff for every
$\lambda $
-coherent iff for every
 $(\gamma ,\delta )\in [\kappa ]^2$
,
$(\gamma ,\delta )\in [\kappa ]^2$
,  $$ \begin{align*}|\{\alpha<\gamma\mathrel{|} c(\alpha,\gamma)\neq c(\alpha,\delta)\}|<\lambda.\end{align*} $$
$$ \begin{align*}|\{\alpha<\gamma\mathrel{|} c(\alpha,\gamma)\neq c(\alpha,\delta)\}|<\lambda.\end{align*} $$
-
(3) For
 $S\subseteq \operatorname {\mathrm {acc}}(\kappa )$
,Footnote
3
c is S-coherent iff for all
$S\subseteq \operatorname {\mathrm {acc}}(\kappa )$
,Footnote
3
c is S-coherent iff for all
 $\beta \le \gamma <\delta <\kappa $
with
$\beta \le \gamma <\delta <\kappa $
with
 $\beta \in S$
,
$\beta \in S$
,  $$ \begin{align*}\sup\{\alpha<\beta\mathrel{|} c(\alpha,\gamma)\neq c(\alpha,\delta)\}<\beta.\end{align*} $$
$$ \begin{align*}\sup\{\alpha<\beta\mathrel{|} c(\alpha,\gamma)\neq c(\alpha,\delta)\}<\beta.\end{align*} $$
Remark 3.25. For every
![]() $\lambda \in \operatorname {\mathrm {Reg}}(\kappa )$
, c is
$\lambda \in \operatorname {\mathrm {Reg}}(\kappa )$
, c is
![]() $\lambda $
-coherent iff it is
$\lambda $
-coherent iff it is
![]() $E^{\kappa }_{\lambda }$
-coherent iff it is
$E^{\kappa }_{\lambda }$
-coherent iff it is
![]() $E^{\kappa }_{\ge \lambda }$
-coherent.
$E^{\kappa }_{\ge \lambda }$
-coherent.
Lemma 3.26. Let
![]() $c:[\kappa ]^2\rightarrow \theta $
be a coloring, with
$c:[\kappa ]^2\rightarrow \theta $
be a coloring, with
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
.
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
.
-
(1) If c is
 $\theta $
-coherent, then it is
$\theta $
-coherent, then it is
 $\ell _{\infty }$
-coherent.
$\ell _{\infty }$
-coherent. -
(2) If c is subadditive, then it is
 $\partial (c)$
-coherent and
$\partial (c)$
-coherent and
 $\ell _{\infty }$
-coherent.
$\ell _{\infty }$
-coherent. -
(3) If c is
 $\ell _{\infty }$
-coherent, then it is weakly subadditive.
$\ell _{\infty }$
-coherent, then it is weakly subadditive.
Proof (1) If c is
![]() $\theta $
-coherent, then for all
$\theta $
-coherent, then for all
![]() $\gamma <\delta <\kappa $
,
$\gamma <\delta <\kappa $
,
is
![]() $< \theta $
, and, for every
$< \theta $
, and, for every
![]() $i\in [j,\theta )$
,
$i\in [j,\theta )$
,
![]() $D^c_{\le i}(\gamma )=D^c_{\le i}(\delta )\cap \gamma $
.
$D^c_{\le i}(\gamma )=D^c_{\le i}(\delta )\cap \gamma $
.
(2) Suppose that c is subadditive. To see that c is
![]() $\ell _{\infty }$
-coherent, let
$\ell _{\infty }$
-coherent, let
![]() $\gamma <\delta <\kappa $
be arbitrary. Set
$\gamma <\delta <\kappa $
be arbitrary. Set
![]() $j:=c(\gamma ,\delta )$
. For all
$j:=c(\gamma ,\delta )$
. For all
![]() $i<\theta $
and
$i<\theta $
and
![]() $\alpha \in D^c_{\le i}(\gamma )$
,
$\alpha \in D^c_{\le i}(\gamma )$
,
![]() $c(\alpha ,\delta )\le \max \{c(\alpha ,\gamma ),c(\gamma ,\delta )\}\le \max \{i,j\}$
, and, for all
$c(\alpha ,\delta )\le \max \{c(\alpha ,\gamma ),c(\gamma ,\delta )\}\le \max \{i,j\}$
, and, for all
![]() $i<\theta $
and
$i<\theta $
and
![]() $\alpha \in D^c_{\le i}(\delta )\cap \gamma $
,
$\alpha \in D^c_{\le i}(\delta )\cap \gamma $
,
![]() $c(\alpha ,\gamma )\le \max \{c(\alpha ,\delta ),c(\gamma ,\delta )\}\le \max \{i,j\}$
. Altogether,
$c(\alpha ,\gamma )\le \max \{c(\alpha ,\delta ),c(\gamma ,\delta )\}\le \max \{i,j\}$
. Altogether,
![]() $D^c_{\le i}(\gamma )=D^c_{\le i}(\delta )\cap \gamma $
for every
$D^c_{\le i}(\gamma )=D^c_{\le i}(\delta )\cap \gamma $
for every
![]() $i\in [j,\theta )$
.
$i\in [j,\theta )$
.
Next, we show that c is
![]() $\partial (c)$
-coherent. To this end, fix
$\partial (c)$
-coherent. To this end, fix
![]() $\beta \leq \gamma < \delta < \kappa $
with
$\beta \leq \gamma < \delta < \kappa $
with
![]() $\beta \in \partial (S)$
. Set
$\beta \in \partial (S)$
. Set
![]() $i := c(\gamma , \delta )$
. By the subadditivity of c, it follows that
$i := c(\gamma , \delta )$
. By the subadditivity of c, it follows that
![]() $D^c_{\leq j}(\gamma ) = D^c_{\leq j}(\delta ) \cap \gamma $
for all
$D^c_{\leq j}(\gamma ) = D^c_{\leq j}(\delta ) \cap \gamma $
for all
![]() $j \in [i, \theta )$
. In particular,
$j \in [i, \theta )$
. In particular,
![]() $\{\alpha < \beta \mathrel {|} c(\alpha , \gamma ) \neq c(\alpha , \delta )\} \subseteq D^c_{\le i}(\gamma )\cap \beta $
. Since
$\{\alpha < \beta \mathrel {|} c(\alpha , \gamma ) \neq c(\alpha , \delta )\} \subseteq D^c_{\le i}(\gamma )\cap \beta $
. Since
![]() $\beta \in \partial (c)$
,
$\beta \in \partial (c)$
,
![]() $\sup (D^c_{\le i}(\gamma )\cap \beta )<\beta $
, so we are done.
$\sup (D^c_{\le i}(\gamma )\cap \beta )<\beta $
, so we are done.
(3) This is clear.
Corollary 3.27. If
![]() $\lambda $
is regular and
$\lambda $
is regular and
![]() $c:[\lambda ^+]^2\rightarrow \lambda $
is locally small, then
$c:[\lambda ^+]^2\rightarrow \lambda $
is locally small, then
![]() $\partial (c)=E^{\lambda ^+}_{\lambda }$
, and hence:
$\partial (c)=E^{\lambda ^+}_{\lambda }$
, and hence:
-
(1) c is a witness to
 $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\lambda ,\lambda )$
;
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\lambda ,\lambda )$
; -
(2) if c is subadditive, then c is
 $\lambda $
-coherent.
$\lambda $
-coherent.
Proof The fact that
![]() $\partial (c) = E^{\lambda ^+}_{\lambda }$
is immediate. Now, Clause (1) follows from Lemma 3.23, and Clause (2) follows from Lemma 3.26(2).
$\partial (c) = E^{\lambda ^+}_{\lambda }$
is immediate. Now, Clause (1) follows from Lemma 3.23, and Clause (2) follows from Lemma 3.26(2).
Lemma 3.28. Let
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. Either of the following implies that
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. Either of the following implies that
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}} (\kappa , 2,\theta ,2)$
holds:
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}} (\kappa , 2,\theta ,2)$
holds:
-
(1) There exists a
 $\theta $
-coherent witness to
$\theta $
-coherent witness to
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. -
(2)
 $\theta $
is uncountable, and there exists an
$\theta $
is uncountable, and there exists an
 $\ell _{\infty }$
-coherent witness to
$\ell _{\infty }$
-coherent witness to
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
Proof (1) By Clause (2) and Lemma 3.26(1), we may assume here that
![]() $\theta =\omega $
; however, the proof works uniformly. Suppose that
$\theta =\omega $
; however, the proof works uniformly. Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
is a
$c:[\kappa ]^2\rightarrow \theta $
is a
![]() $\theta $
-coherent witness to
$\theta $
-coherent witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. Define a coloring
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. Define a coloring
![]() $d:[\kappa ]^2\rightarrow \theta $
by letting, for all
$d:[\kappa ]^2\rightarrow \theta $
by letting, for all
![]() $\gamma <\delta <\kappa $
,
$\gamma <\delta <\kappa $
,
![]() $d(\gamma ,\delta )$
be the least
$d(\gamma ,\delta )$
be the least
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $D^c_{\le i}(\gamma )=D^c_{\le i}(\delta )\cap \gamma $
for every
$D^c_{\le i}(\gamma )=D^c_{\le i}(\delta )\cap \gamma $
for every
![]() $i\in [j,\theta )$
. It is clear that d is subadditive. Now, if d fails to witness
$i\in [j,\theta )$
. It is clear that d is subadditive. Now, if d fails to witness
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, then we may fix
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, then we may fix
![]() $A\in [\kappa ]^{\kappa }$
and
$A\in [\kappa ]^{\kappa }$
and
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $d(\gamma ,\delta )\le j$
for every pair
$d(\gamma ,\delta )\le j$
for every pair
![]() $(\gamma ,\delta )\in [A]^2$
. For every
$(\gamma ,\delta )\in [A]^2$
. For every
![]() $\gamma \in A$
, let
$\gamma \in A$
, let
![]() $\gamma ':=\min (A\setminus (\gamma +1))$
and
$\gamma ':=\min (A\setminus (\gamma +1))$
and
![]() $i_{\gamma }:=c(\gamma ,\gamma ')$
. Fix
$i_{\gamma }:=c(\gamma ,\gamma ')$
. Fix
![]() $A'\in [A]^{\kappa }$
and
$A'\in [A]^{\kappa }$
and
![]() $i<\theta $
such that
$i<\theta $
such that
![]() $i=\max \{j,i_{\gamma }\}$
for all
$i=\max \{j,i_{\gamma }\}$
for all
![]() $\gamma \in A'$
.
$\gamma \in A'$
.
Then, for every
![]() $(\gamma ,\delta )\in [A']^2$
,
$(\gamma ,\delta )\in [A']^2$
,
![]() $\gamma <\gamma '\le \delta $
and
$\gamma <\gamma '\le \delta $
and
![]() $\gamma \in D^c_{\le i_{\gamma }}(\gamma ')\subseteq D^c_{\le i}(\gamma ')= D^c_{\le i}(\delta )\cap \gamma '$
, so
$\gamma \in D^c_{\le i_{\gamma }}(\gamma ')\subseteq D^c_{\le i}(\gamma ')= D^c_{\le i}(\delta )\cap \gamma '$
, so
![]() $c(\gamma ,\delta )\le i$
. It follows that
$c(\gamma ,\delta )\le i$
. It follows that
![]() $c"[A']^2$
is bounded in
$c"[A']^2$
is bounded in
![]() $\theta $
, contradicting the fact that c witnesses
$\theta $
, contradicting the fact that c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
(2) Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
is an
$c:[\kappa ]^2\rightarrow \theta $
is an
![]() $\ell _{\infty }$
-coherent witness to
$\ell _{\infty }$
-coherent witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
and
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
and
![]() $\theta>\aleph _0$
. For every
$\theta>\aleph _0$
. For every
![]() $j<\theta $
, let
$j<\theta $
, let
![]() $\tau _j$
denote the least indecomposable ordinal greater than j. For every
$\tau _j$
denote the least indecomposable ordinal greater than j. For every
![]() $(\gamma ,\delta )\in [\kappa ]^2$
, let
$(\gamma ,\delta )\in [\kappa ]^2$
, let
![]() $j_{\gamma ,\delta }$
denote the least
$j_{\gamma ,\delta }$
denote the least
![]() $j<\theta $
such that, for all
$j<\theta $
such that, for all
![]() $i<\theta $
,
$i<\theta $
,
![]() $D^c_{\le i}(\gamma +1)\subseteq D^c_{\le i+j}(\delta +1)$
and
$D^c_{\le i}(\gamma +1)\subseteq D^c_{\le i+j}(\delta +1)$
and
![]() $D^c_{\le i}(\delta +1)\cap (\gamma +1)\subseteq D^c_{\le i+j}(\gamma +1)$
. Finally, define a coloring
$D^c_{\le i}(\delta +1)\cap (\gamma +1)\subseteq D^c_{\le i+j}(\gamma +1)$
. Finally, define a coloring
![]() $d:[\kappa ]^2\rightarrow \theta $
via
$d:[\kappa ]^2\rightarrow \theta $
via
![]() $d(\gamma ,\delta ):=\tau _{j_{\gamma ,\delta }}$
.
$d(\gamma ,\delta ):=\tau _{j_{\gamma ,\delta }}$
.
Claim 3.28.1. Let
![]() $\beta <\gamma <\delta <\kappa $
. Then:
$\beta <\gamma <\delta <\kappa $
. Then:
-
(i)
 $d(\beta ,\delta )\le \max \{d(\beta ,\gamma ),d(\gamma ,\delta )\}$
;
$d(\beta ,\delta )\le \max \{d(\beta ,\gamma ),d(\gamma ,\delta )\}$
; -
(ii)
 $d(\beta ,\gamma )\le \max \{d(\beta ,\delta ),d(\gamma ,\delta )\}$
.
$d(\beta ,\gamma )\le \max \{d(\beta ,\delta ),d(\gamma ,\delta )\}$
.
Proof (i) For all
![]() $i<\theta $
,
$i<\theta $
,
![]() $D^c_{\le i}(\beta +1)\subseteq D^c_{\le i+j_{\beta ,\gamma }}(\gamma +1)\subseteq D^c_{\le i+j_{\beta ,\gamma }+j_{\gamma ,\delta }}(\delta +1)$
and
$D^c_{\le i}(\beta +1)\subseteq D^c_{\le i+j_{\beta ,\gamma }}(\gamma +1)\subseteq D^c_{\le i+j_{\beta ,\gamma }+j_{\gamma ,\delta }}(\delta +1)$
and
![]() $D^c_{\le i}(\delta +1)\cap (\beta +1)\subseteq D^c_{\le i+j_{\gamma ,\delta }}(\gamma +1)\cap (\beta +1)\subseteq D^c_{\le i+j_{\gamma ,\delta }+j_{\beta ,\gamma }}(\beta +1)$
. Therefore,
$D^c_{\le i}(\delta +1)\cap (\beta +1)\subseteq D^c_{\le i+j_{\gamma ,\delta }}(\gamma +1)\cap (\beta +1)\subseteq D^c_{\le i+j_{\gamma ,\delta }+j_{\beta ,\gamma }}(\beta +1)$
. Therefore,
![]() $j_{\beta ,\delta }$
is no more than
$j_{\beta ,\delta }$
is no more than
![]() $j:=\max \{j_{\beta ,\gamma }+j_{\gamma ,\delta },j_{\gamma ,\delta }+j_{\beta ,\gamma }\}$
. As
$j:=\max \{j_{\beta ,\gamma }+j_{\gamma ,\delta },j_{\gamma ,\delta }+j_{\beta ,\gamma }\}$
. As
![]() $\tau :=\max \{d(\beta ,\gamma ),d(\gamma ,\delta )\}$
is an indecomposable ordinal greater than both
$\tau :=\max \{d(\beta ,\gamma ),d(\gamma ,\delta )\}$
is an indecomposable ordinal greater than both
![]() $j_{\beta ,\gamma }$
and
$j_{\beta ,\gamma }$
and
![]() $j_{\gamma ,\delta }$
, it is moreover greater than j. Altogether,
$j_{\gamma ,\delta }$
, it is moreover greater than j. Altogether,
![]() $d(\beta ,\delta )=\tau _{j_{\beta ,\delta }}\le \tau _j\le \tau $
.
$d(\beta ,\delta )=\tau _{j_{\beta ,\delta }}\le \tau _j\le \tau $
.
(ii) For all
![]() $i<\theta $
,
$i<\theta $
,
![]() $D^c_{\le i}(\beta +1)\subseteq D^c_{\le i+j_{\beta ,\delta }}(\delta +1)\cap (\gamma +1)\subseteq D^c_{\le i+j_{\beta ,\delta }+j_{\gamma ,\delta }}(\gamma +1)$
and
$D^c_{\le i}(\beta +1)\subseteq D^c_{\le i+j_{\beta ,\delta }}(\delta +1)\cap (\gamma +1)\subseteq D^c_{\le i+j_{\beta ,\delta }+j_{\gamma ,\delta }}(\gamma +1)$
and
![]() $D^c_{\le i}(\gamma +1)\cap (\beta +1)\subseteq D^c_{\le i+j_{\gamma ,\delta }}(\delta +1)\cap (\beta +1)\subseteq D^c_{\le i+j_{\gamma ,\delta }+j_{\beta ,\delta }}(\beta +1)$
. Therefore,
$D^c_{\le i}(\gamma +1)\cap (\beta +1)\subseteq D^c_{\le i+j_{\gamma ,\delta }}(\delta +1)\cap (\beta +1)\subseteq D^c_{\le i+j_{\gamma ,\delta }+j_{\beta ,\delta }}(\beta +1)$
. Therefore,
![]() $j_{\beta ,\gamma }$
is no more than
$j_{\beta ,\gamma }$
is no more than
![]() $j:=\max \{j_{\beta ,\delta }+j_{\gamma ,\delta },j_{\gamma ,\delta }+j_{\beta ,\delta }\}$
. As
$j:=\max \{j_{\beta ,\delta }+j_{\gamma ,\delta },j_{\gamma ,\delta }+j_{\beta ,\delta }\}$
. As
![]() $\tau :=\max \{d(\beta ,\delta ),d(\gamma ,\delta )\}$
is an indecomposable ordinal greater than both
$\tau :=\max \{d(\beta ,\delta ),d(\gamma ,\delta )\}$
is an indecomposable ordinal greater than both
![]() $j_{\beta ,\delta }$
and
$j_{\beta ,\delta }$
and
![]() $j_{\gamma ,\delta }$
, it is moreover greater than j. Altogether,
$j_{\gamma ,\delta }$
, it is moreover greater than j. Altogether,
![]() $d(\beta ,\gamma )=\tau _{j_{\beta ,\gamma }}\le \tau _j\le \tau $
.
$d(\beta ,\gamma )=\tau _{j_{\beta ,\gamma }}\le \tau _j\le \tau $
.
Now, if d fails to witness
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, then we may fix
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, then we may fix
![]() $A\in [\kappa ]^{\kappa }$
and
$A\in [\kappa ]^{\kappa }$
and
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $d(\gamma ,\delta )\le j$
for every pair
$d(\gamma ,\delta )\le j$
for every pair
![]() $(\gamma ,\delta )\in [A]^2$
. By possibly increasing j and thinning out A, we may moreover assume that for every
$(\gamma ,\delta )\in [A]^2$
. By possibly increasing j and thinning out A, we may moreover assume that for every
![]() $\gamma \in A$
,
$\gamma \in A$
,
![]() $c(\gamma ,\gamma +1)\le j$
and
$c(\gamma ,\gamma +1)\le j$
and
![]() $D^c_{\le i}(\gamma +1)\cap \gamma \subseteq D^c_{\le i+j}(\gamma )$
for all
$D^c_{\le i}(\gamma +1)\cap \gamma \subseteq D^c_{\le i+j}(\gamma )$
for all
![]() $i<\theta $
. It follows that for every
$i<\theta $
. It follows that for every
![]() $(\gamma ,\delta )\in [A]^2$
,
$(\gamma ,\delta )\in [A]^2$
,
![]() $\gamma \in D^c_{\le j}(\gamma +1)\cap \delta \subseteq D^c_{\le j+j}(\delta +1)\cap \delta \subseteq D^c_{\le j+j+j}(\delta )$
, so that
$\gamma \in D^c_{\le j}(\gamma +1)\cap \delta \subseteq D^c_{\le j+j}(\delta +1)\cap \delta \subseteq D^c_{\le j+j+j}(\delta )$
, so that
![]() $c"[A]^2\le j\cdot 3<\theta $
, contradicting the fact that c witnesses
$c"[A]^2\le j\cdot 3<\theta $
, contradicting the fact that c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
Corollary 3.29. If there exists a uniformly coherent
![]() $\kappa $
-Souslin tree, then, for every
$\kappa $
-Souslin tree, then, for every
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
,
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
,
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
holds.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,\theta )$
holds.
Proof Suppose that there exists a uniformly coherent
![]() $\kappa $
-Souslin tree. This means that there exists a downward closed subfamily
$\kappa $
-Souslin tree. This means that there exists a downward closed subfamily
![]() $T\subseteq {}^{<\kappa }2$
such that:
$T\subseteq {}^{<\kappa }2$
such that:
-
(a)
 $(T,{\subseteq })$
is a
$(T,{\subseteq })$
is a
 $\kappa $
-Souslin tree;
$\kappa $
-Souslin tree; -
(b) for all
 $s,t\in T$
,
$s,t\in T$
,
 $\{ \epsilon \in \operatorname {\mathrm {dom}}(s)\cap \operatorname {\mathrm {dom}}(t)\mathrel {|} s(\epsilon )\neq t(\epsilon )\}$
is finite;
$\{ \epsilon \in \operatorname {\mathrm {dom}}(s)\cap \operatorname {\mathrm {dom}}(t)\mathrel {|} s(\epsilon )\neq t(\epsilon )\}$
is finite; -
(c) for all
 $s,t\in T$
, if
$s,t\in T$
, if
 $\operatorname {\mathrm {dom}}(s)<\operatorname {\mathrm {dom}}(t)$
, then
$\operatorname {\mathrm {dom}}(s)<\operatorname {\mathrm {dom}}(t)$
, then
 $s*t:=s\cup (t\mathbin \upharpoonright (\operatorname {\mathrm {dom}}(t)\setminus \operatorname {\mathrm {dom}}(s)))$
is in T.
$s*t:=s\cup (t\mathbin \upharpoonright (\operatorname {\mathrm {dom}}(t)\setminus \operatorname {\mathrm {dom}}(s)))$
is in T.
Claim 3.29.1. There exists a downward closed subfamily
![]() $\hat T\subseteq {}^{<\kappa }\kappa $
satisfying (a)–(c), in addition to the following:
$\hat T\subseteq {}^{<\kappa }\kappa $
satisfying (a)–(c), in addition to the following:
-
(d) For all
 $t\in \hat T\cap {}^{\alpha }\kappa $
and
$t\in \hat T\cap {}^{\alpha }\kappa $
and
 $i<\alpha $
,
$i<\alpha $
,
 $t{}^{\smallfrown }\langle i\rangle \in \hat T$
.
$t{}^{\smallfrown }\langle i\rangle \in \hat T$
.
Proof The proof is similar to that of [Reference König14, Theorem 3.6]. Denote
![]() $T_{\alpha }:=T\cap {}^{\alpha }\kappa $
for all
$T_{\alpha }:=T\cap {}^{\alpha }\kappa $
for all
![]() $\alpha < \kappa $
. By a standard fact, we may fix a club
$\alpha < \kappa $
. By a standard fact, we may fix a club
![]() $E\subseteq \kappa $
such that, for every
$E\subseteq \kappa $
such that, for every
![]() $(\alpha ,\beta )\in [E]^2$
, every node in
$(\alpha ,\beta )\in [E]^2$
, every node in
![]() $T_{\alpha }$
admits at least
$T_{\alpha }$
admits at least
![]() $|\alpha |$
-many extensions in
$|\alpha |$
-many extensions in
![]() $T_{\beta }$
. We may also assume that
$T_{\beta }$
. We may also assume that
![]() $0\in E$
. Let
$0\in E$
. Let
![]() $\pi :\kappa \leftrightarrow E$
denote the order-preserving bijection, and denote
$\pi :\kappa \leftrightarrow E$
denote the order-preserving bijection, and denote
![]() $T':=\bigcup _{\alpha <\kappa }T_{\pi (\alpha )}$
. Our next goal is to define a map
$T':=\bigcup _{\alpha <\kappa }T_{\pi (\alpha )}$
. Our next goal is to define a map
![]() $\Pi :T'\rightarrow {}^{<\kappa }\kappa $
such that all of the following hold:
$\Pi :T'\rightarrow {}^{<\kappa }\kappa $
such that all of the following hold:
-
(1) For all
 $\alpha <\kappa $
and
$\alpha <\kappa $
and
 $t\in T_{\pi (\alpha )}$
,
$t\in T_{\pi (\alpha )}$
,
 $\Pi (t)\in {}^{\alpha }\kappa $
.
$\Pi (t)\in {}^{\alpha }\kappa $
. -
(2) For all
 $s\subsetneq t$
from
$s\subsetneq t$
from
 $T'$
,
$T'$
,
 $\Pi (s)\subsetneq \Pi (t)$
.
$\Pi (s)\subsetneq \Pi (t)$
. -
(3) For all
 $s,t\in T'$
, if
$s,t\in T'$
, if
 $\operatorname {\mathrm {dom}}(s)<\operatorname {\mathrm {dom}}(t)$
, then
$\operatorname {\mathrm {dom}}(s)<\operatorname {\mathrm {dom}}(t)$
, then
 $\Pi (s*t)=\Pi (s)*\Pi (t)$
.
$\Pi (s*t)=\Pi (s)*\Pi (t)$
.
We shall define
![]() $\Pi \mathbin \upharpoonright T_{\pi (\alpha )}$
by recursion on
$\Pi \mathbin \upharpoonright T_{\pi (\alpha )}$
by recursion on
![]() $\alpha <\kappa $
:
$\alpha <\kappa $
:
-
▸ For
 $\alpha =0$
, we have
$\alpha =0$
, we have
 $T_{\pi (\alpha )}=T_0=\{\emptyset \}$
, so we set
$T_{\pi (\alpha )}=T_0=\{\emptyset \}$
, so we set
 $\Pi (\emptyset ):=\emptyset $
.
$\Pi (\emptyset ):=\emptyset $
. -
▸ For
 $\alpha =\bar \alpha +1$
such that
$\alpha =\bar \alpha +1$
such that
 $\Pi \mathbin \upharpoonright T_{\pi (\bar \alpha )}$
has been successfully defined, we first fix
$\Pi \mathbin \upharpoonright T_{\pi (\bar \alpha )}$
has been successfully defined, we first fix
 $\bar t\in T_{\pi (\bar \alpha )}$
. Find a cardinal
$\bar t\in T_{\pi (\bar \alpha )}$
. Find a cardinal
 $\mu \ge |\bar \alpha |$
and an injective enumeration
$\mu \ge |\bar \alpha |$
and an injective enumeration
 $\langle t^i\mathrel {|} i<\mu \rangle $
of all the extensions of
$\langle t^i\mathrel {|} i<\mu \rangle $
of all the extensions of
 $\bar t$
in
$\bar t$
in
 $T_{\pi (\alpha )}$
. Finally, for every
$T_{\pi (\alpha )}$
. Finally, for every
 $t\in T_{\pi (\alpha )}$
, find the unique
$t\in T_{\pi (\alpha )}$
, find the unique
 $i<\mu $
such that
$i<\mu $
such that
 $\bar t * t=t^i$
, and then let
$\bar t * t=t^i$
, and then let
 $\Pi (t):=\Pi (t\mathbin \upharpoonright \bar \alpha ){}^{\smallfrown }\langle i\rangle $
. It is clear that Properties (1)–(3) are preserved.
$\Pi (t):=\Pi (t\mathbin \upharpoonright \bar \alpha ){}^{\smallfrown }\langle i\rangle $
. It is clear that Properties (1)–(3) are preserved. -
▸ For
 $\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
such that
$\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
such that
 $\Pi \mathbin \upharpoonright T_{\pi (\bar \alpha )}$
has been successfully defined for all
$\Pi \mathbin \upharpoonright T_{\pi (\bar \alpha )}$
has been successfully defined for all
 $\bar \alpha <\alpha $
, we just let
$\bar \alpha <\alpha $
, we just let
 $\Pi (t):=\bigcup \{\Pi (t\mathbin \upharpoonright \pi (\bar \alpha ))\mathrel {|} \bar \alpha <\alpha \}$
for every
$\Pi (t):=\bigcup \{\Pi (t\mathbin \upharpoonright \pi (\bar \alpha ))\mathrel {|} \bar \alpha <\alpha \}$
for every
 $t\in T_{\pi (\alpha )}$
. It is clear that Properties (1)–(3) are preserved.
$t\in T_{\pi (\alpha )}$
. It is clear that Properties (1)–(3) are preserved.
Set
![]() $\hat T:=\operatorname {\mathrm {Im}}(\Pi )$
. By Property (2),
$\hat T:=\operatorname {\mathrm {Im}}(\Pi )$
. By Property (2),
![]() $(\hat T,{\subseteq })$
is order-isomorphic to
$(\hat T,{\subseteq })$
is order-isomorphic to
![]() $(T',{\subseteq })$
which is a
$(T',{\subseteq })$
which is a
![]() $\kappa $
-sized subtree of
$\kappa $
-sized subtree of
![]() $(T,{\subseteq })$
, so
$(T,{\subseteq })$
, so
![]() $(\hat T,{\subseteq })$
is indeed a
$(\hat T,{\subseteq })$
is indeed a
![]() $\kappa $
-Souslin tree. By Properties (3) and (b), for all
$\kappa $
-Souslin tree. By Properties (3) and (b), for all
![]() $s,t\in \hat T$
,
$s,t\in \hat T$
,
![]() $\{ \epsilon \in \operatorname {\mathrm {dom}}(s)\cap \operatorname {\mathrm {dom}}(t)\mathrel {|} s(\epsilon )\neq t(\epsilon )\}$
is finite. By Properties (3) and (c), for all
$\{ \epsilon \in \operatorname {\mathrm {dom}}(s)\cap \operatorname {\mathrm {dom}}(t)\mathrel {|} s(\epsilon )\neq t(\epsilon )\}$
is finite. By Properties (3) and (c), for all
![]() $s,t\in \hat T$
, if
$s,t\in \hat T$
, if
![]() $\operatorname {\mathrm {dom}}(s)<\operatorname {\mathrm {dom}}(t)$
, then
$\operatorname {\mathrm {dom}}(s)<\operatorname {\mathrm {dom}}(t)$
, then
![]() $s*t:=s\cup (t\mathbin \upharpoonright (\operatorname {\mathrm {dom}}(t)\setminus \operatorname {\mathrm {dom}}(s)))$
is in
$s*t:=s\cup (t\mathbin \upharpoonright (\operatorname {\mathrm {dom}}(t)\setminus \operatorname {\mathrm {dom}}(s)))$
is in
![]() $\hat T$
. Finally, by the definition of
$\hat T$
. Finally, by the definition of
![]() $\Pi \mathbin \upharpoonright T_{\pi (\alpha )}$
for successor ordinals
$\Pi \mathbin \upharpoonright T_{\pi (\alpha )}$
for successor ordinals
![]() $\alpha <\kappa $
, and by Property (c), it is indeed the case that, for all
$\alpha <\kappa $
, and by Property (c), it is indeed the case that, for all
![]() $t\in \hat T\cap {}^{\alpha }\kappa $
and
$t\in \hat T\cap {}^{\alpha }\kappa $
and
![]() $i<\alpha $
,
$i<\alpha $
,
![]() $t{}^{\smallfrown }\langle i\rangle \in \hat T$
.
$t{}^{\smallfrown }\langle i\rangle \in \hat T$
.
Let
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. By Lemmas 3.28 and 3.2(2), in order to show that
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. By Lemmas 3.28 and 3.2(2), in order to show that
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2, \theta ,\theta )$
holds, it suffices to find a
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2, \theta ,\theta )$
holds, it suffices to find a
![]() $\theta $
-coherent witness to
$\theta $
-coherent witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. To this end, fix
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. To this end, fix
![]() $\hat T$
as in the preceding claim, and then fix some sequence
$\hat T$
as in the preceding claim, and then fix some sequence
![]() $\langle t_{\beta }\mathrel {|} \beta <\kappa \rangle $
such that
$\langle t_{\beta }\mathrel {|} \beta <\kappa \rangle $
such that
![]() $t_{\beta } \in \hat T\cap {}^{\beta }\kappa $
for all
$t_{\beta } \in \hat T\cap {}^{\beta }\kappa $
for all
![]() $\beta < \kappa $
. Define a coloring
$\beta < \kappa $
. Define a coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
via
$c:[\kappa ]^2\rightarrow \theta $
via
 $$ \begin{align*}c(\alpha,\beta):=\begin{cases}t_{\beta}(\alpha),&\text{if }t_{\beta}(\alpha)<\theta,\\ 0,&\text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}c(\alpha,\beta):=\begin{cases}t_{\beta}(\alpha),&\text{if }t_{\beta}(\alpha)<\theta,\\ 0,&\text{otherwise}. \end{cases}\end{align*} $$
Evidently, c is
![]() $\omega $
-coherent. Now, given
$\omega $
-coherent. Now, given
![]() $A\in [\kappa ]^{\kappa }$
, we claim that
$A\in [\kappa ]^{\kappa }$
, we claim that
![]() $c"[A]^2=\theta $
. To see this, let
$c"[A]^2=\theta $
. To see this, let
![]() $i<\theta $
, and note that
$i<\theta $
, and note that
![]() $S:=\{ t_{\alpha }{}^{\smallfrown }\langle i\rangle \mathrel {|} \alpha \in A\setminus \theta \}$
forms a subset of
$S:=\{ t_{\alpha }{}^{\smallfrown }\langle i\rangle \mathrel {|} \alpha \in A\setminus \theta \}$
forms a subset of
![]() $\hat T$
of size
$\hat T$
of size
![]() $\kappa $
, and hence it cannot be an antichain. Pick
$\kappa $
, and hence it cannot be an antichain. Pick
![]() $s,t\in S$
such that
$s,t\in S$
such that
![]() $s\subsetneq t$
. Let
$s\subsetneq t$
. Let
![]() $(\alpha ,\beta )\in [A]^2$
be such that
$(\alpha ,\beta )\in [A]^2$
be such that
![]() $s=t_{\alpha }{}^{\smallfrown }\langle i\rangle $
and
$s=t_{\alpha }{}^{\smallfrown }\langle i\rangle $
and
![]() $t=t_{\beta }{}^{\smallfrown }\langle i\rangle $
. As
$t=t_{\beta }{}^{\smallfrown }\langle i\rangle $
. As
![]() $t_{\alpha }{}^{\smallfrown }\langle i \rangle $
and
$t_{\alpha }{}^{\smallfrown }\langle i \rangle $
and
![]() $t_{\beta }$
are both initial segments of t, we infer that
$t_{\beta }$
are both initial segments of t, we infer that
![]() $t_{\beta }(\alpha )=i$
, and hence
$t_{\beta }(\alpha )=i$
, and hence
![]() $c(\alpha ,\beta )=i$
, as sought.
$c(\alpha ,\beta )=i$
, as sought.
Remark 3.30. By [Reference Brodsky and Rinot3, Theorem C], for every singular cardinal
![]() $\lambda $
,
$\lambda $
,
![]() ${\square (\lambda ^+)}+{\textsf{GCH}}$
entails the existence of a uniformly coherent
${\square (\lambda ^+)}+{\textsf{GCH}}$
entails the existence of a uniformly coherent
![]() $\lambda ^+$
-Souslin tree. By Fact 3.15 and the preceding corollary, the same conclusion does not follow from
$\lambda ^+$
-Souslin tree. By Fact 3.15 and the preceding corollary, the same conclusion does not follow from
![]() ${\square (\lambda ^+,2)}+{\textsf{GCH}}$
.
${\square (\lambda ^+,2)}+{\textsf{GCH}}$
.
We now show that the existence of a coloring c for which
![]() $\partial (c)$
is stationary is in fact equivalent to the existence of a nonreflecting stationary subset of
$\partial (c)$
is stationary is in fact equivalent to the existence of a nonreflecting stationary subset of
![]() $E^{\kappa }_{\theta }$
.
$E^{\kappa }_{\theta }$
.
Lemma 3.31. For a subset
![]() $S\subseteq E^{\kappa }_{\theta }$
, the following are equivalent:
$S\subseteq E^{\kappa }_{\theta }$
, the following are equivalent:
-
(1) For every
 $\gamma \in E^{\kappa }_{>\omega }$
,
$\gamma \in E^{\kappa }_{>\omega }$
,
 $S\cap \gamma $
is nonstationary in
$S\cap \gamma $
is nonstationary in
 $\gamma $
.
$\gamma $
. -
(2) There exists a coloring
 $c:[\kappa ]^2\rightarrow \theta $
for which
$c:[\kappa ]^2\rightarrow \theta $
for which
 $\partial (c)\supseteq S$
.
$\partial (c)\supseteq S$
. -
(3) There exists an S-coherent, closed coloring
 $c:[\kappa ]^2\rightarrow \theta $
for which
$c:[\kappa ]^2\rightarrow \theta $
for which
 $\partial (c)\supseteq S$
.
$\partial (c)\supseteq S$
.
Proof
![]() $(3)\implies (2)$
: This is trivial.
$(3)\implies (2)$
: This is trivial.
![]() $(2)\implies (1)$
: Suppose that
$(2)\implies (1)$
: Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
is a coloring for which
$c:[\kappa ]^2\rightarrow \theta $
is a coloring for which
![]() $\partial (c)\supseteq S$
. Towards a contradiction, suppose that we are given
$\partial (c)\supseteq S$
. Towards a contradiction, suppose that we are given
![]() $\gamma \in E^{\kappa }_{>\omega }$
such that
$\gamma \in E^{\kappa }_{>\omega }$
such that
![]() $S\cap \gamma $
is stationary in
$S\cap \gamma $
is stationary in
![]() $\gamma $
. As
$\gamma $
. As
![]() $S\subseteq E^{\kappa }_{\theta }$
, it follows that
$S\subseteq E^{\kappa }_{\theta }$
, it follows that
![]() $\operatorname {\mathrm {cf}}(\gamma )>\theta $
, and hence
$\operatorname {\mathrm {cf}}(\gamma )>\theta $
, and hence
![]() $\gamma \notin \partial (c)$
. As
$\gamma \notin \partial (c)$
. As
![]() $\operatorname {\mathrm {cf}}(\gamma )\neq \theta $
, we may pick
$\operatorname {\mathrm {cf}}(\gamma )\neq \theta $
, we may pick
![]() $i<\theta $
such that
$i<\theta $
such that
![]() $\sup (D^c_{\le i}(\gamma ))=\gamma $
. Now, pick
$\sup (D^c_{\le i}(\gamma ))=\gamma $
. Now, pick
![]() $\beta \in \operatorname {\mathrm {acc}}^+(D^c_{\le i}(\gamma ))\cap S$
. It follows that
$\beta \in \operatorname {\mathrm {acc}}^+(D^c_{\le i}(\gamma ))\cap S$
. It follows that
![]() $\sup (D^c_{\le i}(\gamma )\cap \beta )=\beta $
, contradicting the fact that
$\sup (D^c_{\le i}(\gamma )\cap \beta )=\beta $
, contradicting the fact that
![]() $\beta \in S\subseteq \partial (c)$
.
$\beta \in S\subseteq \partial (c)$
.
![]() $(1)\implies (3)$
: Pick a C-sequence
$(1)\implies (3)$
: Pick a C-sequence
![]() $\vec C=\langle C_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
such that, for all
$\vec C=\langle C_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
such that, for all
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $\operatorname {\mathrm {otp}}(C_{\alpha })=\operatorname {\mathrm {cf}}(\alpha )$
and
$\operatorname {\mathrm {otp}}(C_{\alpha })=\operatorname {\mathrm {cf}}(\alpha )$
and
![]() $\operatorname {\mathrm {acc}}(C_{\alpha })\cap S=\emptyset $
. Let
$\operatorname {\mathrm {acc}}(C_{\alpha })\cap S=\emptyset $
. Let
![]() $\operatorname {\mathrm {tr}}$
be the function derived from
$\operatorname {\mathrm {tr}}$
be the function derived from
![]() $\vec C$
as in [Reference Lambie-Hanson and Rinot20, Definition 4.4]. Define a coloring
$\vec C$
as in [Reference Lambie-Hanson and Rinot20, Definition 4.4]. Define a coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
via
$c:[\kappa ]^2\rightarrow \theta $
via
By [Reference Lambie-Hanson and Rinot20, Lemma 4.7], c is closed.
Claim 3.31.1. Let
![]() $\beta <\gamma <\kappa $
with
$\beta <\gamma <\kappa $
with
![]() $\beta \in S$
. Then there exists
$\beta \in S$
. Then there exists
![]() $\epsilon <\beta $
such that, for every
$\epsilon <\beta $
such that, for every
![]() $\alpha \in (\epsilon ,\beta )$
,
$\alpha \in (\epsilon ,\beta )$
,
![]() $c(\alpha ,\gamma )=c(\alpha ,\beta )\ge \operatorname {\mathrm {otp}}(C_{\beta }\cap \alpha )$
.
$c(\alpha ,\gamma )=c(\alpha ,\beta )\ge \operatorname {\mathrm {otp}}(C_{\beta }\cap \alpha )$
.
Proof For every
![]() $\alpha < \beta $
, since
$\alpha < \beta $
, since
![]() $\beta \in \operatorname {\mathrm {Im}}(\operatorname {\mathrm {tr}}(\alpha ,\beta ))$
and
$\beta \in \operatorname {\mathrm {Im}}(\operatorname {\mathrm {tr}}(\alpha ,\beta ))$
and
![]() $\operatorname {\mathrm {otp}}(C_{\beta }\cap \alpha )< \operatorname {\mathrm {otp}}(C_{\beta })=\theta $
, it is immediate that
$\operatorname {\mathrm {otp}}(C_{\beta }\cap \alpha )< \operatorname {\mathrm {otp}}(C_{\beta })=\theta $
, it is immediate that
![]() $c(\alpha ,\beta )\ge \operatorname {\mathrm {otp}}(C_{\beta }\cap \alpha )$
. Set
$c(\alpha ,\beta )\ge \operatorname {\mathrm {otp}}(C_{\beta }\cap \alpha )$
. Set
![]() $j:=c(\beta ,\gamma )$
, and then fix a large enough
$j:=c(\beta ,\gamma )$
, and then fix a large enough
![]() $\epsilon <\beta $
such that
$\epsilon <\beta $
such that
![]() $j\le \operatorname {\mathrm {otp}}(C_{\beta }\cap \epsilon )$
and
$j\le \operatorname {\mathrm {otp}}(C_{\beta }\cap \epsilon )$
and
![]() $\lambda (\beta ,\gamma )\le \epsilon $
.Footnote
4
$\lambda (\beta ,\gamma )\le \epsilon $
.Footnote
4
Let
![]() $\alpha \in (\epsilon ,\beta )$
. Then
$\alpha \in (\epsilon ,\beta )$
. Then
![]() $\operatorname {\mathrm {tr}}(\alpha ,\gamma )=\operatorname {\mathrm {tr}}(\beta ,\gamma ){}^{\smallfrown }\operatorname {\mathrm {tr}}(\alpha ,\beta )$
, and hence
$\operatorname {\mathrm {tr}}(\alpha ,\gamma )=\operatorname {\mathrm {tr}}(\beta ,\gamma ){}^{\smallfrown }\operatorname {\mathrm {tr}}(\alpha ,\beta )$
, and hence
In particular,
![]() $c(\alpha ,\gamma )\ge c(\alpha ,\beta )\ge \operatorname {\mathrm {otp}}(C_{\beta }\cap \alpha )\ge j$
. Now, as
$c(\alpha ,\gamma )\ge c(\alpha ,\beta )\ge \operatorname {\mathrm {otp}}(C_{\beta }\cap \alpha )\ge j$
. Now, as
 $$ \begin{align*} j=c(\beta,\gamma)=&\sup(\{ \operatorname{\mathrm{otp}}(C_{\eta}\cap\beta)\mathrel{|} \eta\in\operatorname{\mathrm{Im}}(\operatorname{\mathrm{tr}}(\beta,\gamma))\}\cap\theta)\\ \ge&\sup(\{ \operatorname{\mathrm{otp}}(C_{\eta}\cap\alpha)\mathrel{|} \eta\in\operatorname{\mathrm{Im}}(\operatorname{\mathrm{tr}}(\beta,\gamma))\}\cap\theta), \end{align*} $$
$$ \begin{align*} j=c(\beta,\gamma)=&\sup(\{ \operatorname{\mathrm{otp}}(C_{\eta}\cap\beta)\mathrel{|} \eta\in\operatorname{\mathrm{Im}}(\operatorname{\mathrm{tr}}(\beta,\gamma))\}\cap\theta)\\ \ge&\sup(\{ \operatorname{\mathrm{otp}}(C_{\eta}\cap\alpha)\mathrel{|} \eta\in\operatorname{\mathrm{Im}}(\operatorname{\mathrm{tr}}(\beta,\gamma))\}\cap\theta), \end{align*} $$
it follows that
as sought.
It now immediately follows that
![]() $\partial (c)\supseteq S$
and that c is S-coherent.
$\partial (c)\supseteq S$
and that c is S-coherent.
Remark 3.32. By Fact 3.15, the preceding lemma cannot be strengthened to assert that the existence of a nonreflecting stationary subset of
![]() $E^{\kappa }_{\theta }$
gives rise to a subadditive coloring
$E^{\kappa }_{\theta }$
gives rise to a subadditive coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
for which
$c:[\kappa ]^2\rightarrow \theta $
for which
![]() $\partial (c)$
is stationary. In fact, a nonreflecting stationary subset of
$\partial (c)$
is stationary. In fact, a nonreflecting stationary subset of
![]() $E^{\kappa }_{\theta }$
is not even enough to imply the existence of a coloring
$E^{\kappa }_{\theta }$
is not even enough to imply the existence of a coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
such that
$c:[\kappa ]^2\rightarrow \theta $
such that
![]() $\partial (c)$
is stationary and c is weakly subadditive of the first kind. This is because, by Theorem 3.45,
$\partial (c)$
is stationary and c is weakly subadditive of the first kind. This is because, by Theorem 3.45,
![]() $\textsf {PFA}$
implies that, for example, any witness to
$\textsf {PFA}$
implies that, for example, any witness to
![]() $\operatorname {\mathrm {U}}(\omega _3,2,\omega ,2)$
is not weakly subadditive of the first kind, whereas, by a result of Beaudoin (see the remark at the end of [Reference Ben-David and Magidor1, Section 2]),
$\operatorname {\mathrm {U}}(\omega _3,2,\omega ,2)$
is not weakly subadditive of the first kind, whereas, by a result of Beaudoin (see the remark at the end of [Reference Ben-David and Magidor1, Section 2]),
![]() $\textsf {PFA}$
is consistent with the existence of a nonreflecting stationary subset of
$\textsf {PFA}$
is consistent with the existence of a nonreflecting stationary subset of
![]() $E^{\omega _3}_{\omega }$
.
$E^{\omega _3}_{\omega }$
.
By Lemmas 3.14(1) and 3.27(2), for every infinite regular cardinal
![]() $\lambda $
, there exists a locally small coloring
$\lambda $
, there exists a locally small coloring
![]() $c:[\lambda ^+]^2\rightarrow \lambda $
that is
$c:[\lambda ^+]^2\rightarrow \lambda $
that is
![]() $\lambda $
-coherent. We shall now prove that for every singular cardinal
$\lambda $
-coherent. We shall now prove that for every singular cardinal
![]() $\lambda $
, a locally small coloring
$\lambda $
, a locally small coloring
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
is never
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
is never
![]() $\operatorname {\mathrm {cf}}(\lambda )$
-coherent. Assuming that c is subadditive of the first kind (which is indeed possible, by Lemma 3.13), even weaker forms of coherence are not feasible.
$\operatorname {\mathrm {cf}}(\lambda )$
-coherent. Assuming that c is subadditive of the first kind (which is indeed possible, by Lemma 3.13), even weaker forms of coherence are not feasible.
Lemma 3.33. Suppose that
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
is a locally small coloring.
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
is a locally small coloring.
-
(1) If
 $\lambda $
is regular or if c is subadditive of the first kind, then for every cardinal
$\lambda $
is regular or if c is subadditive of the first kind, then for every cardinal
 $\theta <\lambda $
, c is not
$\theta <\lambda $
, c is not
 $\theta $
-coherent.
$\theta $
-coherent. -
(2) If
 $\lambda $
is singular, then c is not
$\lambda $
is singular, then c is not
 $\operatorname {\mathrm {cf}}(\lambda )$
-coherent.
$\operatorname {\mathrm {cf}}(\lambda )$
-coherent.
Proof The proof is similar to that of [Reference König14, Theorem 3.7]. Suppose for the sake of contradiction that c is
![]() $\theta $
-coherent for some fixed cardinal
$\theta $
-coherent for some fixed cardinal
![]() $\theta <\lambda $
and that either c is subadditive of the first kind or
$\theta <\lambda $
and that either c is subadditive of the first kind or
![]() $\theta \leq \operatorname {\mathrm {cf}}(\lambda )$
.
$\theta \leq \operatorname {\mathrm {cf}}(\lambda )$
.
Claim 3.33.1. For every
![]() $\gamma <\lambda ^+$
, there exists
$\gamma <\lambda ^+$
, there exists
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
such that
$i<\operatorname {\mathrm {cf}}(\lambda )$
such that
Proof Let
![]() $\gamma <\lambda ^+$
. Denote
$\gamma <\lambda ^+$
. Denote
![]() $\delta :=\gamma +\lambda $
. First, since
$\delta :=\gamma +\lambda $
. First, since
![]() $\operatorname {\mathrm {otp}}([\gamma ,\delta ))=\lambda>\theta $
, we may let
$\operatorname {\mathrm {otp}}([\gamma ,\delta ))=\lambda>\theta $
, we may let
Second, if
![]() $\theta \le \operatorname {\mathrm {cf}}(\lambda )$
, then, since c is
$\theta \le \operatorname {\mathrm {cf}}(\lambda )$
, then, since c is
![]() $\theta $
-coherent,
$\theta $
-coherent,
is an ordinal
![]() $<\operatorname {\mathrm {cf}}(\lambda )$
. If
$<\operatorname {\mathrm {cf}}(\lambda )$
. If
![]() $\theta>\operatorname {\mathrm {cf}}(\lambda )$
, then we instead let
$\theta>\operatorname {\mathrm {cf}}(\lambda )$
, then we instead let
![]() $i_1:=c(\gamma ,\delta )$
.
$i_1:=c(\gamma ,\delta )$
.
We claim that
![]() $i:=\max \{i_0,i_1\}$
is as sought.
$i:=\max \{i_0,i_1\}$
is as sought.
-
▸ If
 $\theta \le \operatorname {\mathrm {cf}}(\lambda )$
, then for every
$\theta \le \operatorname {\mathrm {cf}}(\lambda )$
, then for every
 $\alpha \in D^c_{\le i}(\gamma )$
, either
$\alpha \in D^c_{\le i}(\gamma )$
, either
 $c(\alpha ,\delta )\le i_1\le i$
or
$c(\alpha ,\delta )\le i_1\le i$
or
 $c(\alpha ,\delta )=c(\alpha ,\gamma )\le i$
. Therefore,
$c(\alpha ,\delta )=c(\alpha ,\gamma )\le i$
. Therefore,
 $D^c_{\le i}(\gamma )\subseteq D^c_{\le i}(\delta )$
.
$D^c_{\le i}(\gamma )\subseteq D^c_{\le i}(\delta )$
. -
▸ Otherwise, c is subadditive of the first kind and
 $i_i = c(\gamma , \delta )$
. Then, for every
$i_i = c(\gamma , \delta )$
. Then, for every
 $\alpha \in D^c_{\le i}(\gamma )$
, we have
$\alpha \in D^c_{\le i}(\gamma )$
, we have
 $c(\alpha ,\delta )\le \max \{c(\alpha ,\gamma ),c(\gamma ,\delta )\}\le \max \{c(\alpha ,\gamma ),i_1\}\le i$
, so that
$c(\alpha ,\delta )\le \max \{c(\alpha ,\gamma ),c(\gamma ,\delta )\}\le \max \{c(\alpha ,\gamma ),i_1\}\le i$
, so that
 $\alpha \in D^c_{\le i}(\delta )$
. Thus, again,
$\alpha \in D^c_{\le i}(\delta )$
. Thus, again,
 $D^c_{\le i}(\gamma )\subseteq D^c_{\le i}(\delta )$
.
$D^c_{\le i}(\gamma )\subseteq D^c_{\le i}(\delta )$
.
Now, set
![]() $x:=D^c_{\le i}(\delta )\setminus \gamma $
, and notice that
$x:=D^c_{\le i}(\delta )\setminus \gamma $
, and notice that
![]() $\operatorname {\mathrm {otp}}(x)\ge \operatorname {\mathrm {otp}}(D^c_{\le i_0}(\delta )\setminus \gamma )\ge \theta +1$
. Altogether
$\operatorname {\mathrm {otp}}(x)\ge \operatorname {\mathrm {otp}}(D^c_{\le i_0}(\delta )\setminus \gamma )\ge \theta +1$
. Altogether
![]() $D^c_{\le i}(\gamma )\uplus x\subseteq D^c_{\le i}(\delta )$
with
$D^c_{\le i}(\gamma )\uplus x\subseteq D^c_{\le i}(\delta )$
with
![]() $D^c_{\le i}(\gamma )\subseteq \min (x)$
, and hence
$D^c_{\le i}(\gamma )\subseteq \min (x)$
, and hence
![]() $\operatorname {\mathrm {otp}}(D^c_{\le i}(\gamma ))+\theta +1\le \operatorname {\mathrm {otp}}(D^c_{\le i}(\delta ))$
.
$\operatorname {\mathrm {otp}}(D^c_{\le i}(\gamma ))+\theta +1\le \operatorname {\mathrm {otp}}(D^c_{\le i}(\delta ))$
.
By the claim, for each
![]() $\gamma <\lambda ^+$
, we may fix
$\gamma <\lambda ^+$
, we may fix
![]() $i_{\gamma }<\operatorname {\mathrm {cf}}(\lambda )$
such that
$i_{\gamma }<\operatorname {\mathrm {cf}}(\lambda )$
such that
![]() $\operatorname {\mathrm {otp}}(D^c_{\le i_{\gamma }}(\gamma ))+\theta <\operatorname {\mathrm {otp}}(D^c_{\le i_{\gamma }}(\gamma +\lambda ))$
. Fix a sparse enough stationary subset
$\operatorname {\mathrm {otp}}(D^c_{\le i_{\gamma }}(\gamma ))+\theta <\operatorname {\mathrm {otp}}(D^c_{\le i_{\gamma }}(\gamma +\lambda ))$
. Fix a sparse enough stationary subset
![]() $S\subseteq \lambda ^+$
along with
$S\subseteq \lambda ^+$
along with
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
such that
$i<\operatorname {\mathrm {cf}}(\lambda )$
such that
![]() $i_{\gamma }=i$
for all
$i_{\gamma }=i$
for all
![]() $\gamma \in S$
, and such that
$\gamma \in S$
, and such that
![]() $\beta +\lambda <\gamma $
for all
$\beta +\lambda <\gamma $
for all
![]() $(\beta ,\gamma )\in [S]^2$
. Define a map
$(\beta ,\gamma )\in [S]^2$
. Define a map
![]() $f:S\rightarrow \lambda $
via
$f:S\rightarrow \lambda $
via
Let
![]() $(\beta ,\gamma )\in [S]^2$
. As
$(\beta ,\gamma )\in [S]^2$
. As
![]() $\beta +\lambda <\gamma $
and c is
$\beta +\lambda <\gamma $
and c is
![]() $\theta $
-coherent,
$\theta $
-coherent,
Altogether,
Therefore, f is an injection from a set of size
![]() $\lambda ^+$
to
$\lambda ^+$
to
![]() $\lambda $
, which is a contradiction.
$\lambda $
, which is a contradiction.
We conclude this subsection by introducing a notion of forcing that adds a subadditive coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
whose
$c:[\kappa ]^2\rightarrow \theta $
whose
![]() $\partial (c)$
is stationary. This will prove Clause (1) of Theorem C.
$\partial (c)$
is stationary. This will prove Clause (1) of Theorem C.
Theorem 3.34. Suppose that
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. Then:
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. Then:
-
(1) There exists a
 $\theta ^+$
-directed closed,
$\theta ^+$
-directed closed,
 $\kappa $
-strategically closed forcing notion
$\kappa $
-strategically closed forcing notion
 $\mathbb P$
that adds an
$\mathbb P$
that adds an
 $E^{\kappa }_{\geq \theta }$
-closed, subadditive coloring
$E^{\kappa }_{\geq \theta }$
-closed, subadditive coloring
 $c:[\kappa ]^2\rightarrow \theta $
for which
$c:[\kappa ]^2\rightarrow \theta $
for which
 $\partial (c)$
is stationary. In particular,
$\partial (c)$
is stationary. In particular,
 $\Vdash _{\mathbb P}"\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )."$
$\Vdash _{\mathbb P}"\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )."$
-
(2) If
 $\kappa = \lambda ^+$
and
$\kappa = \lambda ^+$
and
 $\operatorname {\mathrm {cf}}(\lambda ) = \theta < \lambda $
, then there is also a
$\operatorname {\mathrm {cf}}(\lambda ) = \theta < \lambda $
, then there is also a
 $\theta ^+$
-directed closed,
$\theta ^+$
-directed closed,
 $(\lambda +1)$
-strategically closed
$(\lambda +1)$
-strategically closed
 $($
hence
$($
hence
 $({<}\kappa )$
-distributive
$({<}\kappa )$
-distributive
 $)$
forcing notion
$)$
forcing notion
 $\mathbb P$
that adds a coloring as above which is moreover locally small.
$\mathbb P$
that adds a coloring as above which is moreover locally small.
Proof In Case (2), let
![]() $\langle \lambda _i \mathrel {|} i < \theta \rangle $
be an increasing sequence of regular cardinals converging to
$\langle \lambda _i \mathrel {|} i < \theta \rangle $
be an increasing sequence of regular cardinals converging to
![]() $\lambda $
, with
$\lambda $
, with
![]() $\lambda _i> \theta $
. In Case (1), simply let
$\lambda _i> \theta $
. In Case (1), simply let
![]() $\lambda _i := \kappa $
for all
$\lambda _i := \kappa $
for all
![]() $i < \theta $
.
$i < \theta $
.
We will define a forcing notion
![]() $\mathbb {P}$
whose generic object will generate a coloring c as above. Our poset
$\mathbb {P}$
whose generic object will generate a coloring c as above. Our poset
![]() $\mathbb {P}$
consists of all subadditive colorings of the form
$\mathbb {P}$
consists of all subadditive colorings of the form
![]() $p : [\gamma _p + 1]^2 \rightarrow \theta $
such that:
$p : [\gamma _p + 1]^2 \rightarrow \theta $
such that:
-
•
 $\gamma _p < \kappa $
;
$\gamma _p < \kappa $
; -
• p is
 $E^{\gamma _p+1}_{\geq \theta }$
-closed;
$E^{\gamma _p+1}_{\geq \theta }$
-closed; -
• for all
 $\beta \leq \gamma _p$
and all
$\beta \leq \gamma _p$
and all
 $i < \theta $
, we have
$i < \theta $
, we have
 $|D^p_{\leq i}(\beta )| < \lambda _i$
.
$|D^p_{\leq i}(\beta )| < \lambda _i$
.
![]() $\mathbb {P}$
is ordered by reverse inclusion. We also include the empty set as the unique maximal condition in
$\mathbb {P}$
is ordered by reverse inclusion. We also include the empty set as the unique maximal condition in
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Claim 3.34.1.
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\theta ^+$
-directed closed.
$\theta ^+$
-directed closed.
Proof Note that
![]() $\mathbb {P}$
is tree-like, i.e., if
$\mathbb {P}$
is tree-like, i.e., if
![]() $p,q,r \in \mathbb {P}$
and r extends both p and q, then p and q are
$p,q,r \in \mathbb {P}$
and r extends both p and q, then p and q are
![]() $\leq _{\mathbb {P}}$
-comparable. It therefore suffices to prove that
$\leq _{\mathbb {P}}$
-comparable. It therefore suffices to prove that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\theta ^+$
-closed. To this end, suppose that
$\theta ^+$
-closed. To this end, suppose that
![]() $\xi < \theta ^+$
and
$\xi < \theta ^+$
and
![]() $\vec {p} = \langle p_{\eta } \mathrel {|} \eta < \xi \rangle $
is a decreasing sequence of conditions in
$\vec {p} = \langle p_{\eta } \mathrel {|} \eta < \xi \rangle $
is a decreasing sequence of conditions in
![]() $\mathbb {P}$
. We may assume without loss of generality that
$\mathbb {P}$
. We may assume without loss of generality that
![]() $\xi $
is an infinite regular cardinal and
$\xi $
is an infinite regular cardinal and
![]() $\vec {p}$
is strictly decreasing, i.e.,
$\vec {p}$
is strictly decreasing, i.e.,
![]() $\langle \gamma _{\eta } \mathrel {|} \eta < \xi \rangle $
is strictly increasing, where
$\langle \gamma _{\eta } \mathrel {|} \eta < \xi \rangle $
is strictly increasing, where
![]() $\gamma _{\eta }$
denotes
$\gamma _{\eta }$
denotes
![]() $\gamma _{p_{\eta }}$
. For all
$\gamma _{p_{\eta }}$
. For all
![]() $\eta < \xi $
, by possibly extending
$\eta < \xi $
, by possibly extending
![]() $p_{\eta }$
to copy some information from
$p_{\eta }$
to copy some information from
![]() $p_{\eta +1}$
, we may also assume that
$p_{\eta +1}$
, we may also assume that
![]() $\gamma _{\eta }$
is a successor ordinal. Let
$\gamma _{\eta }$
is a successor ordinal. Let
![]() $\gamma ^* := \sup \{\gamma _{\eta } \mathrel {|} \eta < \xi \}$
, and let
$\gamma ^* := \sup \{\gamma _{\eta } \mathrel {|} \eta < \xi \}$
, and let
![]() $q^* := \bigcup _{\eta < \xi } p_{\eta }$
. Note that
$q^* := \bigcup _{\eta < \xi } p_{\eta }$
. Note that
![]() $q^*$
is not a condition in
$q^*$
is not a condition in
![]() $\mathbb {P}$
, since its domain is not the square of a successor ordinal. We will extend it to a condition
$\mathbb {P}$
, since its domain is not the square of a successor ordinal. We will extend it to a condition
![]() $q: [\gamma ^* + 1]^2 \rightarrow \theta $
, which will then be a lower bound for
$q: [\gamma ^* + 1]^2 \rightarrow \theta $
, which will then be a lower bound for
![]() $\vec {p}$
. To do so, it suffices to specify
$\vec {p}$
. To do so, it suffices to specify
![]() $q(\alpha , \gamma ^*)$
for all
$q(\alpha , \gamma ^*)$
for all
![]() $\alpha < \gamma ^*$
. There are two cases to consider:
$\alpha < \gamma ^*$
. There are two cases to consider:
![]() $\blacktriangleright $
Assume that
$\blacktriangleright $
Assume that
![]() $\xi < \theta $
. We can then fix an
$\xi < \theta $
. We can then fix an
![]() $i^* < \theta $
such that
$i^* < \theta $
such that
![]() $q^*(\gamma _{\eta }, \gamma _{\eta '}) \leq i^*$
for all
$q^*(\gamma _{\eta }, \gamma _{\eta '}) \leq i^*$
for all
![]() $\eta < \eta ' < \xi $
. Now, given
$\eta < \eta ' < \xi $
. Now, given
![]() $\alpha < \gamma ^*$
, let
$\alpha < \gamma ^*$
, let
![]() $\eta _{\alpha } < \xi $
be the least
$\eta _{\alpha } < \xi $
be the least
![]() $\eta $
for which
$\eta $
for which
![]() $\alpha < \gamma _{\eta }$
and then set
$\alpha < \gamma _{\eta }$
and then set
![]() $q(\alpha , \gamma ^*) := \max \{i^*, q^*(\alpha , \gamma _{\eta _{\alpha }})\}$
. It is straightforward to prove, using our choice of
$q(\alpha , \gamma ^*) := \max \{i^*, q^*(\alpha , \gamma _{\eta _{\alpha }})\}$
. It is straightforward to prove, using our choice of
![]() $i^*$
and the fact that each
$i^*$
and the fact that each
![]() $p_{\eta }$
is subadditive, that the coloring q thus defined is also subadditive.
$p_{\eta }$
is subadditive, that the coloring q thus defined is also subadditive.
Since each
![]() $p_{\eta }$
is
$p_{\eta }$
is
![]() $E^{\gamma _{\eta } + 1}_{\geq \theta }$
-closed, in order to show that q is
$E^{\gamma _{\eta } + 1}_{\geq \theta }$
-closed, in order to show that q is
![]() $E^{\gamma ^*+1}_{\geq \theta }$
-closed, it suffices to prove that for all
$E^{\gamma ^*+1}_{\geq \theta }$
-closed, it suffices to prove that for all
![]() $A \subseteq \gamma ^*$
and all
$A \subseteq \gamma ^*$
and all
![]() $i < \theta $
such that
$i < \theta $
such that
![]() $A \subseteq D^{q}_{\leq i}(\gamma ^*)$
and
$A \subseteq D^{q}_{\leq i}(\gamma ^*)$
and
![]() $\sup (A) \in E^{\gamma ^*}_{\geq \theta }$
, we have
$\sup (A) \in E^{\gamma ^*}_{\geq \theta }$
, we have
![]() $\sup (A) \in D^{q}_{\leq i}(\gamma ^*)$
. To this end, fix such an A and i. Let
$\sup (A) \in D^{q}_{\leq i}(\gamma ^*)$
. To this end, fix such an A and i. Let
![]() $\beta := \sup (A)$
. By our choice of
$\beta := \sup (A)$
. By our choice of
![]() $i^*$
, we know that
$i^*$
, we know that
![]() $i \geq i^*$
and
$i \geq i^*$
and
![]() $q(\alpha , \gamma ^*) = \max \{i^*, p_{\eta _{\beta }}(\alpha , \gamma _{\eta _{\beta }})\}$
for all
$q(\alpha , \gamma ^*) = \max \{i^*, p_{\eta _{\beta }}(\alpha , \gamma _{\eta _{\beta }})\}$
for all
![]() $\alpha \in A \cup \{\beta \}$
. By the fact that
$\alpha \in A \cup \{\beta \}$
. By the fact that
![]() $p_{\eta _{\beta }}$
is
$p_{\eta _{\beta }}$
is
![]() $E^{\gamma _{\eta _{\beta }+1}}_{\geq \theta }$
-closed, we know that
$E^{\gamma _{\eta _{\beta }+1}}_{\geq \theta }$
-closed, we know that
![]() $p_{\eta _{\beta }}(\beta ) \leq i$
, so
$p_{\eta _{\beta }}(\beta ) \leq i$
, so
![]() $\beta \in D^{q}_{\leq i}(\gamma ^*)$
.
$\beta \in D^{q}_{\leq i}(\gamma ^*)$
.
To show that q is a condition, it remains only to verify that
![]() $|D^{q}_{\leq i}(\gamma ^*)| < \lambda _i$
for all
$|D^{q}_{\leq i}(\gamma ^*)| < \lambda _i$
for all
![]() $i < \theta $
. To this end, fix
$i < \theta $
. To this end, fix
![]() $i < \theta $
. By our construction, we have
$i < \theta $
. By our construction, we have
![]() $D^{q}_{\leq i}(\gamma ^*) \subseteq \bigcup _{\eta < \xi } D^{p_{\eta }}_{\leq i}(\gamma _{\eta })$
. Since
$D^{q}_{\leq i}(\gamma ^*) \subseteq \bigcup _{\eta < \xi } D^{p_{\eta }}_{\leq i}(\gamma _{\eta })$
. Since
![]() $\xi < \lambda _i$
and
$\xi < \lambda _i$
and
![]() $\lambda _i$
is regular, the fact that each
$\lambda _i$
is regular, the fact that each
![]() $p_{\eta }$
is a condition in
$p_{\eta }$
is a condition in
![]() $\mathbb {P}$
then implies that
$\mathbb {P}$
then implies that
![]() $|D^{q}_{\leq i}(\gamma ^*)| < \lambda _i$
.
$|D^{q}_{\leq i}(\gamma ^*)| < \lambda _i$
.
![]() $\blacktriangleright $
Assume that
$\blacktriangleright $
Assume that
![]() $\xi = \theta $
. Fix a strictly increasing sequence
$\xi = \theta $
. Fix a strictly increasing sequence
![]() $\langle i_{\eta } \mathrel {|} \eta < \theta \rangle $
of ordinals below
$\langle i_{\eta } \mathrel {|} \eta < \theta \rangle $
of ordinals below
![]() $\theta $
such that, for all
$\theta $
such that, for all
![]() $\eta < \eta ' < \theta $
, we have
$\eta < \eta ' < \theta $
, we have
![]() $q^*(\gamma _{\eta }, \gamma _{\eta '}) \leq i_{\eta '}$
. Now, given
$q^*(\gamma _{\eta }, \gamma _{\eta '}) \leq i_{\eta '}$
. Now, given
![]() $\alpha < \gamma ^*$
, let
$\alpha < \gamma ^*$
, let
![]() $\eta _{\alpha } < \theta $
be the least
$\eta _{\alpha } < \theta $
be the least
![]() $\eta $
for which
$\eta $
for which
![]() $\alpha < \gamma _{\eta }$
and then set
$\alpha < \gamma _{\eta }$
and then set
![]() $q(\alpha , \gamma ^*) := \max \{i_{\eta _{\alpha }}, q^*(\alpha , \gamma _{\eta _{\alpha }})\}$
. It is again straightforward to prove that the coloring q thus defined is subadditive. The verification involves a case analysis; to illustrate the type of argument involved, we go through the proof of one of the required inequalities in one of the cases, leaving the other similar arguments to the reader.
$q(\alpha , \gamma ^*) := \max \{i_{\eta _{\alpha }}, q^*(\alpha , \gamma _{\eta _{\alpha }})\}$
. It is again straightforward to prove that the coloring q thus defined is subadditive. The verification involves a case analysis; to illustrate the type of argument involved, we go through the proof of one of the required inequalities in one of the cases, leaving the other similar arguments to the reader.
Suppose that
![]() $\alpha < \beta < \gamma ^*$
and we have
$\alpha < \beta < \gamma ^*$
and we have
![]() $\gamma _{\eta _{\alpha }} < \beta $
. We will prove that
$\gamma _{\eta _{\alpha }} < \beta $
. We will prove that
![]() $q(\alpha , \gamma ^*) \leq \max \{q(\alpha , \beta ), q(\beta , \gamma ^*)\}$
. If
$q(\alpha , \gamma ^*) \leq \max \{q(\alpha , \beta ), q(\beta , \gamma ^*)\}$
. If
![]() $q(\alpha , \gamma ^*) = i_{\eta _{\alpha }}$
, then this is trivial, so assume that
$q(\alpha , \gamma ^*) = i_{\eta _{\alpha }}$
, then this is trivial, so assume that
![]() $q(\alpha , \gamma ^*) = q^*(\alpha , \gamma _{\eta _{\alpha }})$
. Now, since each
$q(\alpha , \gamma ^*) = q^*(\alpha , \gamma _{\eta _{\alpha }})$
. Now, since each
![]() $p_{\eta }$
is subadditive (and hence
$p_{\eta }$
is subadditive (and hence
![]() $q^*$
is subadditive), we have
$q^*$
is subadditive), we have
 $$ \begin{align*} q^*(\alpha, \gamma_{\eta_{\alpha}}) &\leq \max\{q^*(\alpha, \beta), ~ q^*(\gamma_{\eta_{\alpha}}, \beta)\} \\ &\leq \max\{q^*(\alpha, \beta), ~ q^*(\gamma_{\eta_{\alpha}}, \gamma_{\eta_{\beta}}), ~ q^*(\beta, \gamma_{\eta_{\beta}})\} \\ &\leq \max\{q^*(\alpha, \beta), ~ i_{\eta_{\beta}}, ~ q^*(\beta, \gamma_{\eta_{\beta}})\} \\ &= \max\{q(\alpha, \beta), ~ q(\beta, \gamma^*)\}. \end{align*} $$
$$ \begin{align*} q^*(\alpha, \gamma_{\eta_{\alpha}}) &\leq \max\{q^*(\alpha, \beta), ~ q^*(\gamma_{\eta_{\alpha}}, \beta)\} \\ &\leq \max\{q^*(\alpha, \beta), ~ q^*(\gamma_{\eta_{\alpha}}, \gamma_{\eta_{\beta}}), ~ q^*(\beta, \gamma_{\eta_{\beta}})\} \\ &\leq \max\{q^*(\alpha, \beta), ~ i_{\eta_{\beta}}, ~ q^*(\beta, \gamma_{\eta_{\beta}})\} \\ &= \max\{q(\alpha, \beta), ~ q(\beta, \gamma^*)\}. \end{align*} $$
Note that the final equality above holds because
![]() $q(\alpha , \beta ) = q^*(\alpha , \beta )$
and
$q(\alpha , \beta ) = q^*(\alpha , \beta )$
and
![]() $q(\beta , \gamma ^*) = \max \{i_{\eta _{\beta }}, q^*(\beta , \gamma _{\eta _{\beta }})\}$
.
$q(\beta , \gamma ^*) = \max \{i_{\eta _{\beta }}, q^*(\beta , \gamma _{\eta _{\beta }})\}$
.
We now verify that q is
![]() $E^{\gamma ^*+1}_{\geq \theta }$
-closed. As in the previous case, we fix an
$E^{\gamma ^*+1}_{\geq \theta }$
-closed. As in the previous case, we fix an
![]() $A \subseteq \gamma ^*$
and an
$A \subseteq \gamma ^*$
and an
![]() $i < \theta $
such that
$i < \theta $
such that
![]() $A \subseteq D^{q}_{\leq i}(\gamma ^*)$
and
$A \subseteq D^{q}_{\leq i}(\gamma ^*)$
and
![]() $\beta := \sup (A)$
is in
$\beta := \sup (A)$
is in
![]() $E^{\gamma ^*}_{\geq \theta }$
. It will suffice to show that
$E^{\gamma ^*}_{\geq \theta }$
. It will suffice to show that
![]() $\beta \in D^{q}_{\leq i}(\gamma ^*)$
. To avoid triviality, assume that
$\beta \in D^{q}_{\leq i}(\gamma ^*)$
. To avoid triviality, assume that
![]() $\beta \notin A$
. Since
$\beta \notin A$
. Since
![]() $\beta $
is a limit ordinal we know that
$\beta $
is a limit ordinal we know that
![]() $\beta $
is not equal to
$\beta $
is not equal to
![]() $\gamma _{\eta }$
for any
$\gamma _{\eta }$
for any
![]() $\eta < \theta $
. It follows that, by passing to a tail of A if necessary, we may assume that
$\eta < \theta $
. It follows that, by passing to a tail of A if necessary, we may assume that
![]() $\eta _{\alpha } = \eta _{\beta }$
for all
$\eta _{\alpha } = \eta _{\beta }$
for all
![]() $\alpha \in A$
. Then, for all
$\alpha \in A$
. Then, for all
![]() $\alpha \in A \cup \{\beta \}$
, we have
$\alpha \in A \cup \{\beta \}$
, we have
![]() $q(\alpha , \gamma ^*) = \max \{i_{\eta _{\beta }}, p_{\gamma _{\beta }}(\alpha , \gamma _{\eta _{\beta }})$
. It follows that
$q(\alpha , \gamma ^*) = \max \{i_{\eta _{\beta }}, p_{\gamma _{\beta }}(\alpha , \gamma _{\eta _{\beta }})$
. It follows that
![]() $i \geq i_{\eta _{\beta }}$
and, since
$i \geq i_{\eta _{\beta }}$
and, since
![]() $p_{\gamma _{\beta }}$
is
$p_{\gamma _{\beta }}$
is
![]() $E^{\gamma _{\beta } + 1}_{\geq \theta }$
-closed, that
$E^{\gamma _{\beta } + 1}_{\geq \theta }$
-closed, that
![]() $p_{\eta _{\beta }}(\beta ) \leq i$
, so
$p_{\eta _{\beta }}(\beta ) \leq i$
, so
![]() $\beta \in D^{q}_{\leq i}(\gamma ^*)$
.
$\beta \in D^{q}_{\leq i}(\gamma ^*)$
.
The fact that
![]() $|D^q_{\leq i}(\gamma ^*)| < \lambda _i$
for all
$|D^q_{\leq i}(\gamma ^*)| < \lambda _i$
for all
![]() $i < \theta $
follows by exactly the same reasoning as in the previous case.
$i < \theta $
follows by exactly the same reasoning as in the previous case.
Let
![]() $\dot {c}$
be the canonical
$\dot {c}$
be the canonical
![]() $\mathbb {P}$
-name for the union of the generic filter. Then
$\mathbb {P}$
-name for the union of the generic filter. Then
![]() $\dot {c}$
is forced to be a subadditive function from an initial segment of
$\dot {c}$
is forced to be a subadditive function from an initial segment of
![]() $[\kappa ]^2$
to
$[\kappa ]^2$
to
![]() $\theta $
(we will see shortly that its domain is forced to be all of
$\theta $
(we will see shortly that its domain is forced to be all of
![]() $[\kappa ]^2$
).
$[\kappa ]^2$
).
Note that in the
![]() $\xi = \theta $
case of the above claim, we actually proved something stronger that will be useful later: if
$\xi = \theta $
case of the above claim, we actually proved something stronger that will be useful later: if
![]() $\vec {p} = \langle p_{\eta } \mathrel {|} \eta < \theta \rangle $
is a strictly decreasing sequence of conditions in
$\vec {p} = \langle p_{\eta } \mathrel {|} \eta < \theta \rangle $
is a strictly decreasing sequence of conditions in
![]() $\mathbb {P}$
and
$\mathbb {P}$
and
![]() $\gamma := \sup \{\gamma _{p_{\eta }} \mathrel {|} \eta < \theta \}$
, then there is a lower bound q for
$\gamma := \sup \{\gamma _{p_{\eta }} \mathrel {|} \eta < \theta \}$
, then there is a lower bound q for
![]() $\vec {p}$
such that
$\vec {p}$
such that
![]() $q \Vdash _{\mathbb {P}} "\gamma \in \partial (\dot {c})."$
$q \Vdash _{\mathbb {P}} "\gamma \in \partial (\dot {c})."$
The next claim will show that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $({<}\kappa )$
-distributive.
$({<}\kappa )$
-distributive.
Claim 3.34.2. In Case (1),
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa $
-strategically closed. In Case (2),
$\kappa $
-strategically closed. In Case (2),
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $(\lambda + 1)$
-strategically closed.
$(\lambda + 1)$
-strategically closed.
Proof In Case (1), denote
![]() $\chi :=\kappa $
. In Case (2), denote
$\chi :=\kappa $
. In Case (2), denote
![]() $\chi :=\lambda $
. We describe a winning strategy for Player II in
$\chi :=\lambda $
. We describe a winning strategy for Player II in
![]() $\Game _{\chi }(\mathbb {P})$
. (Note that, if
$\Game _{\chi }(\mathbb {P})$
. (Note that, if
![]() $\chi = \lambda $
, then it appears that we are just showing that
$\chi = \lambda $
, then it appears that we are just showing that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\lambda $
-strategically closed, but the fact that
$\lambda $
-strategically closed, but the fact that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\theta ^+$
-closed will then show that
$\theta ^+$
-closed will then show that
![]() $\mathbb {P}$
is in fact
$\mathbb {P}$
is in fact
![]() $(\lambda +1)$
-strategically closed.) We will arrange so that, if
$(\lambda +1)$
-strategically closed.) We will arrange so that, if
![]() $\langle p_{\eta } \mathrel {|} \eta < \chi \rangle $
is a play of the game in which Player II plays according to their prescribed strategy, then, letting
$\langle p_{\eta } \mathrel {|} \eta < \chi \rangle $
is a play of the game in which Player II plays according to their prescribed strategy, then, letting
![]() $\gamma _{\eta } := \gamma _{p_{\eta }}$
for all
$\gamma _{\eta } := \gamma _{p_{\eta }}$
for all
![]() $\eta < \chi $
,
$\eta < \chi $
,
-
(a)
 $\langle \gamma _{\eta } \mathrel {|} \eta < \chi \text { is a nonzero even ordinal} \rangle $
is a continuous, strictly increasing sequence;
$\langle \gamma _{\eta } \mathrel {|} \eta < \chi \text { is a nonzero even ordinal} \rangle $
is a continuous, strictly increasing sequence; -
(b) for all even ordinals
 $\eta < \xi < \chi $
, we have
$\eta < \xi < \chi $
, we have
 $p_{\xi }(\gamma _{\eta }, \gamma _{\xi }) = \min \{i < \theta \mathrel {|} \xi < \lambda _i\}$
.
$p_{\xi }(\gamma _{\eta }, \gamma _{\xi }) = \min \{i < \theta \mathrel {|} \xi < \lambda _i\}$
.
Now suppose that
![]() $\xi < \chi $
is an even ordinal and
$\xi < \chi $
is an even ordinal and
![]() $\langle p_{\eta } \mathrel {|} \eta < \xi \rangle $
is a partial run of
$\langle p_{\eta } \mathrel {|} \eta < \xi \rangle $
is a partial run of
![]() $\Game _{\chi }(\mathbb {P})$
that thus far satisfies requirements (a) and (b) above. We will describe a strategy for Player II to choose the next play,
$\Game _{\chi }(\mathbb {P})$
that thus far satisfies requirements (a) and (b) above. We will describe a strategy for Player II to choose the next play,
![]() $p_{\xi }$
, while maintaining (a) and (b).
$p_{\xi }$
, while maintaining (a) and (b).
![]() $\blacktriangleright $
If
$\blacktriangleright $
If
![]() $\xi = 0$
, then we are required to set
$\xi = 0$
, then we are required to set
![]() $p_{\xi } = 1_{\mathbb {P}} = \emptyset $
.
$p_{\xi } = 1_{\mathbb {P}} = \emptyset $
.
![]() $\blacktriangleright $
If
$\blacktriangleright $
If
![]() $\xi = \xi ' + 1$
is a successor ordinal, then, since
$\xi = \xi ' + 1$
is a successor ordinal, then, since
![]() $\xi $
is even, there is another even ordinal
$\xi $
is even, there is another even ordinal
![]() $\xi "$
such that
$\xi "$
such that
![]() $\xi = \xi " + 2$
. Let
$\xi = \xi " + 2$
. Let
![]() $\gamma ^* := \gamma _{\xi '} + 1$
. We will define
$\gamma ^* := \gamma _{\xi '} + 1$
. We will define
![]() $p_{\xi }$
so that
$p_{\xi }$
so that
![]() $\gamma _{\xi } = \gamma ^*$
. To do so, we must define
$\gamma _{\xi } = \gamma ^*$
. To do so, we must define
![]() $p_{\xi }(\alpha , \gamma ^*)$
for all
$p_{\xi }(\alpha , \gamma ^*)$
for all
![]() $\alpha < \gamma ^*$
. We assume that
$\alpha < \gamma ^*$
. We assume that
![]() $\gamma _{\xi "} < \gamma _{\xi '}$
(if they are equal, the construction is similar but easier). Let
$\gamma _{\xi "} < \gamma _{\xi '}$
(if they are equal, the construction is similar but easier). Let
![]() $i^* := \min \{i < \theta \mathrel {|} \xi < \lambda _i\}$
. First, to satisfy (b), we must let
$i^* := \min \{i < \theta \mathrel {|} \xi < \lambda _i\}$
. First, to satisfy (b), we must let
![]() $p_{\xi }(\gamma _{\xi "}, \gamma ^*) := i^*$
. Next, for all
$p_{\xi }(\gamma _{\xi "}, \gamma ^*) := i^*$
. Next, for all
![]() $\alpha < \gamma _{\xi "}$
, let
$\alpha < \gamma _{\xi "}$
, let
![]() $p_{\xi }(\alpha , \gamma ^*) := \max \{p_{\xi "}(\alpha , \gamma _{\xi "}), i^*\}$
. Let
$p_{\xi }(\alpha , \gamma ^*) := \max \{p_{\xi "}(\alpha , \gamma _{\xi "}), i^*\}$
. Let
![]() $i^{**} := \max \{i^*, p_{\xi '}(\gamma _{\xi "}, \gamma _{\xi '})\}$
, and set
$i^{**} := \max \{i^*, p_{\xi '}(\gamma _{\xi "}, \gamma _{\xi '})\}$
, and set
![]() $p(\gamma _{\xi '}, \gamma ^*) := i^{**}$
. Finally, for all
$p(\gamma _{\xi '}, \gamma ^*) := i^{**}$
. Finally, for all
![]() $\alpha \in (\gamma _{\xi "}, \gamma _{\xi '})$
, let
$\alpha \in (\gamma _{\xi "}, \gamma _{\xi '})$
, let
![]() $p_{\xi }(\alpha , \gamma ^*) := \max \{i^{**}, p_{\xi '}(\alpha , \gamma _{\xi '})\}$
. It is easily verified that
$p_{\xi }(\alpha , \gamma ^*) := \max \{i^{**}, p_{\xi '}(\alpha , \gamma _{\xi '})\}$
. It is easily verified that
![]() $p_{\xi }$
thus defined is a condition in
$p_{\xi }$
thus defined is a condition in
![]() $\mathbb {P}$
and that we have continued to satisfy requirements (a) and (b).
$\mathbb {P}$
and that we have continued to satisfy requirements (a) and (b).
![]() $\blacktriangleright $
If
$\blacktriangleright $
If
![]() $\xi $
is a nonzero limit ordinal, then let
$\xi $
is a nonzero limit ordinal, then let
![]() $p^* := \bigcup _{\eta < \xi } p_{\eta }$
, and let
$p^* := \bigcup _{\eta < \xi } p_{\eta }$
, and let
![]() $\gamma ^* := \sup \{\gamma _{\eta } \mathrel {|} \eta < \xi \}$
. We will define a lower bound
$\gamma ^* := \sup \{\gamma _{\eta } \mathrel {|} \eta < \xi \}$
. We will define a lower bound
![]() $p_{\xi }$
for the run of the game so far with
$p_{\xi }$
for the run of the game so far with
![]() $\gamma _{\xi } = \gamma ^*$
. To do so, it suffices to define
$\gamma _{\xi } = \gamma ^*$
. To do so, it suffices to define
![]() $p_{\xi }(\alpha , \gamma ^*)$
for all
$p_{\xi }(\alpha , \gamma ^*)$
for all
![]() $\alpha < \gamma ^*$
. Let
$\alpha < \gamma ^*$
. Let
![]() $i^* := \min \{i < \theta \mathrel {|} \xi < \lambda _i\}$
. For all
$i^* := \min \{i < \theta \mathrel {|} \xi < \lambda _i\}$
. For all
![]() $\alpha < \gamma ^*$
, let
$\alpha < \gamma ^*$
, let
![]() $\eta _{\alpha } < \xi $
be the least even ordinal
$\eta _{\alpha } < \xi $
be the least even ordinal
![]() $\eta $
such that
$\eta $
such that
![]() $\alpha < \gamma _{\eta }$
, and then set
$\alpha < \gamma _{\eta }$
, and then set
![]() $p_{\xi }(\alpha , \gamma ^*) := \max \{i^*, p^*(\alpha , \gamma _{\eta _{\alpha }})\}$
. By the fact that the play of the game thus far satisfied (b), we know that
$p_{\xi }(\alpha , \gamma ^*) := \max \{i^*, p^*(\alpha , \gamma _{\eta _{\alpha }})\}$
. By the fact that the play of the game thus far satisfied (b), we know that
![]() $p^*(\gamma _{\eta }, \gamma _{\eta '}) \leq i^*$
for all even ordinals
$p^*(\gamma _{\eta }, \gamma _{\eta '}) \leq i^*$
for all even ordinals
![]() $\eta < \eta ' < \xi $
, so this definition does in fact ensure that
$\eta < \eta ' < \xi $
, so this definition does in fact ensure that
![]() $p_{\xi }(\gamma _{\eta }, \gamma _{\xi }) = i^*$
, so we have satisfied (b). The fact that the play of the game thus far satisfied (a) and (b) also implies that
$p_{\xi }(\gamma _{\eta }, \gamma _{\xi }) = i^*$
, so we have satisfied (b). The fact that the play of the game thus far satisfied (a) and (b) also implies that
![]() $p_{\xi }$
is subadditive and
$p_{\xi }$
is subadditive and
![]() $E^{\gamma _{\xi }+1}_{\geq \theta }$
-closed and that we have continued to satisfy requirement (a). Finally, to show that
$E^{\gamma _{\xi }+1}_{\geq \theta }$
-closed and that we have continued to satisfy requirement (a). Finally, to show that
![]() $|D^{p_{\xi }}_{\leq i}(\gamma _{\xi })| < \lambda _i$
for all
$|D^{p_{\xi }}_{\leq i}(\gamma _{\xi })| < \lambda _i$
for all
![]() $i < \theta $
, note firstly that
$i < \theta $
, note firstly that
![]() $D^{p_{\xi }}_{\leq i}(\gamma _{\xi }) = \emptyset $
for all
$D^{p_{\xi }}_{\leq i}(\gamma _{\xi }) = \emptyset $
for all
![]() $i < i^*$
and, secondly, that for all
$i < i^*$
and, secondly, that for all
![]() $i \in [i^*, \theta )$
, we have
$i \in [i^*, \theta )$
, we have
![]() $D^{p_{\xi }}_{\leq i}(\gamma _{\xi }) \subseteq \bigcup _{\eta < \xi } D^{p_{\eta }}_{\leq i}(\gamma _{\eta })$
. For each
$D^{p_{\xi }}_{\leq i}(\gamma _{\xi }) \subseteq \bigcup _{\eta < \xi } D^{p_{\eta }}_{\leq i}(\gamma _{\eta })$
. For each
![]() $i \in [i^*, \theta )$
, we know that
$i \in [i^*, \theta )$
, we know that
![]() $\xi < \lambda _i$
and
$\xi < \lambda _i$
and
![]() $\lambda _i$
is regular, so the fact that
$\lambda _i$
is regular, so the fact that
![]() $p_{\eta }$
is a condition for all
$p_{\eta }$
is a condition for all
![]() $\eta < \xi $
implies that
$\eta < \xi $
implies that
![]() $|D^{p_{\xi }}_{\leq i}(\gamma _{\xi })| < \lambda _i$
.
$|D^{p_{\xi }}_{\leq i}(\gamma _{\xi })| < \lambda _i$
.
This completes the description of Player II’s winning strategy and hence the proof of the claim.
By the argument of the proof of the above claim, it follows that, for every
![]() $\alpha < \kappa $
, the set
$\alpha < \kappa $
, the set
![]() $E_{\alpha }$
of
$E_{\alpha }$
of
![]() $p \in \mathbb {P}$
for which
$p \in \mathbb {P}$
for which
![]() $\gamma _p \geq \alpha $
is dense in
$\gamma _p \geq \alpha $
is dense in
![]() $\mathbb {P}$
. Therefore, the domain of
$\mathbb {P}$
. Therefore, the domain of
![]() $\dot {c}$
is forced to be
$\dot {c}$
is forced to be
![]() $[\kappa ]^2$
. The definition of
$[\kappa ]^2$
. The definition of
![]() $\mathbb {P}$
also immediately implies that
$\mathbb {P}$
also immediately implies that
![]() $\dot {c}$
is forced to be
$\dot {c}$
is forced to be
![]() $E^{\kappa }_{\geq \theta }$
-closed and, in Case (2),
$E^{\kappa }_{\geq \theta }$
-closed and, in Case (2),
![]() $\dot {c}$
is also forced to be locally small. We now finish the proof of the theorem by showing that
$\dot {c}$
is also forced to be locally small. We now finish the proof of the theorem by showing that
![]() $\partial (\dot {c})$
is forced to be stationary. (By Lemma 3.23, this will imply that
$\partial (\dot {c})$
is forced to be stationary. (By Lemma 3.23, this will imply that
![]() $\dot {c}$
witnesses
$\dot {c}$
witnesses
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa , \theta , \theta )$
.) To this end, fix a condition p and a
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa , \theta , \theta )$
.) To this end, fix a condition p and a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {D}$
forced to be a club in
$\dot {D}$
forced to be a club in
![]() $\kappa $
. We will find
$\kappa $
. We will find
![]() $q \leq p$
and
$q \leq p$
and
![]() $\gamma < \kappa $
such that
$\gamma < \kappa $
such that
![]() $q \Vdash _{\mathbb {P}}"\gamma \in \dot {D} \cap \partial (\dot {c})."$
$q \Vdash _{\mathbb {P}}"\gamma \in \dot {D} \cap \partial (\dot {c})."$
Using the fact that
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\theta ^+$
-closed and the fact that each
$\theta ^+$
-closed and the fact that each
![]() $E_{\alpha }$
as defined above is dense, fix a decreasing sequence
$E_{\alpha }$
as defined above is dense, fix a decreasing sequence
![]() $\langle p_{\eta } \mathrel {|} \eta < \theta \rangle $
of conditions in
$\langle p_{\eta } \mathrel {|} \eta < \theta \rangle $
of conditions in
![]() $\mathbb {P}$
together with an increasing sequence
$\mathbb {P}$
together with an increasing sequence
![]() $\langle \alpha _{\eta } \mathrel {|} \eta < \theta \rangle $
of ordinals below
$\langle \alpha _{\eta } \mathrel {|} \eta < \theta \rangle $
of ordinals below
![]() $\kappa $
such that:
$\kappa $
such that:
-
(1)
 $p_0 = p$
;
$p_0 = p$
; -
(2) for all
 $\eta < \theta $
,
$\eta < \theta $
,
 $p_{\eta + 1} \Vdash _{\mathbb {P}}"\alpha _{\eta } \in \dot {D}"$
;
$p_{\eta + 1} \Vdash _{\mathbb {P}}"\alpha _{\eta } \in \dot {D}"$
; -
(3) for all
 $\eta < \theta $
,
$\eta < \theta $
,
 $\gamma _{\eta } < \alpha _{\eta } < \gamma _{\eta + 1}$
.
$\gamma _{\eta } < \alpha _{\eta } < \gamma _{\eta + 1}$
.
Now let
![]() $\gamma := \sup \{\gamma _{\eta } \mathrel {|} \eta < \theta \}$
, so that
$\gamma := \sup \{\gamma _{\eta } \mathrel {|} \eta < \theta \}$
, so that
![]() $\gamma = \sup \{\alpha _{\eta } \mathrel {|} \eta < \theta \}$
. By the proof of Claim 3.34.1, we can find a lower bound q for
$\gamma = \sup \{\alpha _{\eta } \mathrel {|} \eta < \theta \}$
. By the proof of Claim 3.34.1, we can find a lower bound q for
![]() $\langle p_{\eta } \mathrel {|} \eta < \theta \rangle $
such that
$\langle p_{\eta } \mathrel {|} \eta < \theta \rangle $
such that
![]() $q \Vdash _{\mathbb {P}}"\gamma \in \partial (\dot {c})."$
For all
$q \Vdash _{\mathbb {P}}"\gamma \in \partial (\dot {c})."$
For all
![]() $\eta < \theta $
, since q extends
$\eta < \theta $
, since q extends
![]() $p_{\eta + 1}$
, q also forces
$p_{\eta + 1}$
, q also forces
![]() $\alpha _{\eta }$
to be in
$\alpha _{\eta }$
to be in
![]() $\dot {D}$
. Since
$\dot {D}$
. Since
![]() $\gamma = \sup \{\alpha _{\eta } \mathrel {|} \eta < \theta \}$
and
$\gamma = \sup \{\alpha _{\eta } \mathrel {|} \eta < \theta \}$
and
![]() $\dot {D}$
is forced to be a club, it follows that q forces
$\dot {D}$
is forced to be a club, it follows that q forces
![]() $\gamma $
to be in
$\gamma $
to be in
![]() $\dot {D}$
. We then have
$\dot {D}$
. We then have
![]() $q \Vdash _{\mathbb {P}}"\gamma \in \dot {D} \cap \partial (\dot {c}),"$
as desired.
$q \Vdash _{\mathbb {P}}"\gamma \in \dot {D} \cap \partial (\dot {c}),"$
as desired.
3.4 Large cardinals and consistency results
In this subsection, we investigate the effect on
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\ldots )$
of certain compactness principles, including stationary reflection, the existence of highly complete or indecomposable ultrafilters, and the P-ideal dichotomy
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\ldots )$
of certain compactness principles, including stationary reflection, the existence of highly complete or indecomposable ultrafilters, and the P-ideal dichotomy
Recall that, for stationary subsets
![]() $S,T$
of
$S,T$
of
![]() $\kappa $
,
$\kappa $
,
![]() $\operatorname {\mathrm {Refl}}(\theta ,S,T)$
asserts that, for every
$\operatorname {\mathrm {Refl}}(\theta ,S,T)$
asserts that, for every
![]() $\theta $
-sized collection
$\theta $
-sized collection
![]() $\mathcal S$
of stationary subsets of S, there exists
$\mathcal S$
of stationary subsets of S, there exists
![]() $\beta \in T\cap E^{\kappa }_{>\omega }$
such that
$\beta \in T\cap E^{\kappa }_{>\omega }$
such that
![]() $S\cap \beta $
is stationary in
$S\cap \beta $
is stationary in
![]() $\beta $
for every
$\beta $
for every
![]() $S\in \mathcal S$
. We write
$S\in \mathcal S$
. We write
![]() $\operatorname {\mathrm {Refl}}(\theta ,S)$
for
$\operatorname {\mathrm {Refl}}(\theta ,S)$
for
![]() $\operatorname {\mathrm {Refl}}(\theta ,S,\kappa )$
.
$\operatorname {\mathrm {Refl}}(\theta ,S,\kappa )$
.
Theorem 3.35. Suppose that
![]() $\Sigma $
is some stationary subset of
$\Sigma $
is some stationary subset of
![]() $\kappa $
,
$\kappa $
,
![]() $c:[\kappa ]^2\rightarrow \theta $
is a
$c:[\kappa ]^2\rightarrow \theta $
is a
![]() $\Sigma $
-closed witness to
$\Sigma $
-closed witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, and
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, and
![]() $\operatorname {\mathrm {Refl}}(\theta ,\Sigma ,\kappa \setminus \partial (c))$
holds. Then:
$\operatorname {\mathrm {Refl}}(\theta ,\Sigma ,\kappa \setminus \partial (c))$
holds. Then:
-
(1) If
 $\kappa $
is
$\kappa $
is
 $\theta $
-inaccessible, then c is not subadditive of the first kind.
$\theta $
-inaccessible, then c is not subadditive of the first kind. -
(2) If
 $\partial (c)$
is stationary, then c is not subadditive.
$\partial (c)$
is stationary, then c is not subadditive. -
(3) If c is locally small, then c is not subadditive.
Proof Suppose that c is subadditive of the first kind. For each
![]() $\alpha <\kappa $
, pick
$\alpha <\kappa $
, pick
![]() $i_{\alpha }<\theta $
, for which the following set is stationary:
$i_{\alpha }<\theta $
, for which the following set is stationary:
Next, using the pigeonhole principle, fix
![]() $H\in [\kappa ]^{\kappa }$
and
$H\in [\kappa ]^{\kappa }$
and
![]() $i<\theta $
such that
$i<\theta $
such that
![]() $i_{\alpha }=i$
for all
$i_{\alpha }=i$
for all
![]() $\alpha \in H$
.
$\alpha \in H$
.
Claim 3.35.1. For every
![]() $A\in [H]^{\theta }$
, there is
$A\in [H]^{\theta }$
, there is
![]() $\beta _A<\kappa $
above
$\beta _A<\kappa $
above
![]() $\sup (A)$
such that
$\sup (A)$
such that
![]() $\sup _{\alpha \in A}c(\alpha ,\beta _A)<\theta $
.
$\sup _{\alpha \in A}c(\alpha ,\beta _A)<\theta $
.
Proof Given
![]() $A\in [H]^{\theta }$
, as
$A\in [H]^{\theta }$
, as
![]() $\operatorname {\mathrm {Refl}}(\theta ,\Sigma ,\kappa \setminus \partial (c))$
holds, we may pick
$\operatorname {\mathrm {Refl}}(\theta ,\Sigma ,\kappa \setminus \partial (c))$
holds, we may pick
![]() $\beta \in \kappa \setminus \partial (c)$
such that
$\beta \in \kappa \setminus \partial (c)$
such that
![]() $S_{\alpha }^i\cap \beta $
is stationary in
$S_{\alpha }^i\cap \beta $
is stationary in
![]() $\beta $
for all
$\beta $
for all
![]() $\alpha \in A$
. Now, as
$\alpha \in A$
. Now, as
![]() $\beta \notin \partial (c)$
, we may find some
$\beta \notin \partial (c)$
, we may find some
![]() $j<\theta $
and
$j<\theta $
and
![]() $\gamma \in [\beta , \kappa )$
such that
$\gamma \in [\beta , \kappa )$
such that
![]() $\sup (D^c_{\le j}(\gamma )) \cap \beta =\beta $
. As c is
$\sup (D^c_{\le j}(\gamma )) \cap \beta =\beta $
. As c is
![]() $\Sigma $
-closed, it follows that there exists a club E in
$\Sigma $
-closed, it follows that there exists a club E in
![]() $\beta $
such that
$\beta $
such that
![]() $E\cap \Sigma \subseteq D^c_{\le j}(\gamma )$
. For every
$E\cap \Sigma \subseteq D^c_{\le j}(\gamma )$
. For every
![]() $\alpha \in A$
, fix
$\alpha \in A$
, fix
![]() $\sigma _{\alpha }\in S^{i}_{\alpha }\cap E$
. Since c is subadditive of the first kind, we have
$\sigma _{\alpha }\in S^{i}_{\alpha }\cap E$
. Since c is subadditive of the first kind, we have
![]() $c(\alpha ,\gamma )\le \max \{c(\alpha ,\sigma _{\alpha }),c(\sigma _{\alpha },\gamma )\}\le \max \{i,j\}$
. So, setting
$c(\alpha ,\gamma )\le \max \{c(\alpha ,\sigma _{\alpha }),c(\sigma _{\alpha },\gamma )\}\le \max \{i,j\}$
. So, setting
![]() $\beta _A = \gamma $
, we have
$\beta _A = \gamma $
, we have
![]() $\sup _{\alpha \in A}c(\alpha ,\beta _A)<\theta $
.
$\sup _{\alpha \in A}c(\alpha ,\beta _A)<\theta $
.
(1) Using Lemma 2.4(1), fix
![]() $\epsilon <\kappa $
such that, for cofinally many
$\epsilon <\kappa $
such that, for cofinally many
![]() $\beta <\kappa $
,
$\beta <\kappa $
,
![]() $\{c(\alpha , \beta ) \mathrel {|} \alpha \in H \cap \epsilon \}$
is unbounded in
$\{c(\alpha , \beta ) \mathrel {|} \alpha \in H \cap \epsilon \}$
is unbounded in
![]() $\theta $
. Assuming that
$\theta $
. Assuming that
![]() $\kappa $
is
$\kappa $
is
![]() $\theta $
-inaccessible, we may find some
$\theta $
-inaccessible, we may find some
![]() $A\in [H\cap \epsilon ]^{\theta }$
such that, for cofinally many
$A\in [H\cap \epsilon ]^{\theta }$
such that, for cofinally many
![]() $\beta <\kappa $
,
$\beta <\kappa $
,
![]() $\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
$\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
![]() $\theta $
. In particular, we may find such a
$\theta $
. In particular, we may find such a
![]() $\beta <\kappa $
above
$\beta <\kappa $
above
![]() $\beta _A$
. Set
$\beta _A$
. Set
![]() $j:=\max \{\sup _{\alpha \in A}c(\alpha ,\beta _A),c(\beta _A,\beta )\}$
. Pick
$j:=\max \{\sup _{\alpha \in A}c(\alpha ,\beta _A),c(\beta _A,\beta )\}$
. Pick
![]() $\alpha \in A$
such that
$\alpha \in A$
such that
![]() $c(\alpha ,\beta )>j$
. As c is subadditive of the first kind,
$c(\alpha ,\beta )>j$
. As c is subadditive of the first kind,
![]() $c(\alpha ,\beta )\le \max \{c(\alpha ,\beta _A),c(\beta _A,\beta )\}\le j$
. This is a contradiction.
$c(\alpha ,\beta )\le \max \{c(\alpha ,\beta _A),c(\beta _A,\beta )\}\le j$
. This is a contradiction.
(2) Suppose that
![]() $\partial (c)$
is stationary, and pick
$\partial (c)$
is stationary, and pick
![]() $\beta \in \operatorname {\mathrm {acc}}^+(H)\cap \partial (c)$
. Fix a cofinal subset A of
$\beta \in \operatorname {\mathrm {acc}}^+(H)\cap \partial (c)$
. Fix a cofinal subset A of
![]() $H\cap \beta $
of size
$H\cap \beta $
of size
![]() $\theta $
. As
$\theta $
. As
![]() $\beta \in \partial (c)$
,
$\beta \in \partial (c)$
,
![]() $\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
$\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
![]() $\theta $
. Note that
$\theta $
. Note that
![]() $\beta _A>\sup (A)=\beta $
. Set
$\beta _A>\sup (A)=\beta $
. Set
![]() $i:=\sup _{\alpha \in A}c(\alpha ,\beta _A)$
. If c were weakly subadditive of the second kind, then we could find
$i:=\sup _{\alpha \in A}c(\alpha ,\beta _A)$
. If c were weakly subadditive of the second kind, then we could find
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $D^c_{\le i}(\beta _A)\cap \beta \subseteq D^c_{\le j}(\beta )$
, contradicting the fact that for every
$D^c_{\le i}(\beta _A)\cap \beta \subseteq D^c_{\le j}(\beta )$
, contradicting the fact that for every
![]() $j<\theta $
, there exists
$j<\theta $
, there exists
![]() $\alpha \in A\subseteq D^c_{\le i}(\beta _A)\cap \beta $
with
$\alpha \in A\subseteq D^c_{\le i}(\beta _A)\cap \beta $
with
![]() $c(\alpha ,\beta )>j$
.
$c(\alpha ,\beta )>j$
.
(3) Suppose that
![]() $\kappa =\lambda ^+$
,
$\kappa =\lambda ^+$
,
![]() $\theta =\operatorname {\mathrm {cf}}(\lambda )$
, and c is locally small. Fix the least
$\theta =\operatorname {\mathrm {cf}}(\lambda )$
, and c is locally small. Fix the least
![]() $\beta <\kappa $
such that
$\beta <\kappa $
such that
![]() $\operatorname {\mathrm {otp}}(H\cap \beta )=\lambda $
. For all
$\operatorname {\mathrm {otp}}(H\cap \beta )=\lambda $
. For all
![]() $\epsilon <\beta $
and
$\epsilon <\beta $
and
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
,
$i<\operatorname {\mathrm {cf}}(\lambda )$
,
![]() $|H\cap [\epsilon ,\beta )|=\lambda>|D^c_{\le i}(\beta )|$
, and hence there exists a cofinal subset A of
$|H\cap [\epsilon ,\beta )|=\lambda>|D^c_{\le i}(\beta )|$
, and hence there exists a cofinal subset A of
![]() $H\cap \beta $
of size
$H\cap \beta $
of size
![]() $\theta $
such that
$\theta $
such that
![]() $\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
$\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
![]() $\theta $
. Now, as in the proof of Clause (3), c cannot be weakly subadditive of the second kind.
$\theta $
. Now, as in the proof of Clause (3), c cannot be weakly subadditive of the second kind.
Corollary 3.36. For every
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
and stationary
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
and stationary
![]() $\Sigma \subseteq E^{\kappa }_{\ge \theta }$
, if
$\Sigma \subseteq E^{\kappa }_{\ge \theta }$
, if
![]() $\operatorname {\mathrm {Refl}}(\theta ,\Sigma )$
holds, then there exists no
$\operatorname {\mathrm {Refl}}(\theta ,\Sigma )$
holds, then there exists no
![]() $\Sigma $
-closed witness to
$\Sigma $
-closed witness to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
.
We next show that the existence of subadditive witnesses to
![]() $\operatorname {\mathrm {U}}(\ldots )$
is ruled out by the existence of certain ultrafilters.
$\operatorname {\mathrm {U}}(\ldots )$
is ruled out by the existence of certain ultrafilters.
Definition 3.37. An ultrafilter U over
![]() $\kappa $
is
$\kappa $
is
![]() $\theta $
-indecomposable if it is uniform and, for every sequence of sets
$\theta $
-indecomposable if it is uniform and, for every sequence of sets
![]() $\langle A_i \mathrel {|} i < \theta \rangle $
satisfying
$\langle A_i \mathrel {|} i < \theta \rangle $
satisfying
![]() $\bigcup _{i < \theta } A_i \in U$
, there is
$\bigcup _{i < \theta } A_i \in U$
, there is
![]() $B \in [\theta ]^{<\theta }$
such that
$B \in [\theta ]^{<\theta }$
such that
![]() $\bigcup _{i \in B} A_i \in U$
.
$\bigcup _{i \in B} A_i \in U$
.
Lemma 3.38. Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
is a witness to
$c:[\kappa ]^2\rightarrow \theta $
is a witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
-
(1) If there exists a
 $\theta ^+$
-complete uniform ultrafilter over
$\theta ^+$
-complete uniform ultrafilter over
 $\kappa $
, then c is not weakly subadditive.
$\kappa $
, then c is not weakly subadditive. -
(2) If there exists a
 $\theta ^+$
-complete uniform ultrafilter over
$\theta ^+$
-complete uniform ultrafilter over
 $\kappa $
and
$\kappa $
and
 $\kappa $
is
$\kappa $
is
 $\theta $
-inaccessible, then c is not weakly subadditive of the first kind.
$\theta $
-inaccessible, then c is not weakly subadditive of the first kind. -
(3) If there exists a
 $\theta $
-indecomposable ultrafilter over
$\theta $
-indecomposable ultrafilter over
 $\kappa $
, then c is not subadditive of the second kind.
$\kappa $
, then c is not subadditive of the second kind.
Proof (1) Suppose that U is a
![]() $\theta ^+$
-complete ultrafilter over
$\theta ^+$
-complete ultrafilter over
![]() $\kappa $
. For all
$\kappa $
. For all
![]() $\alpha <\kappa $
and
$\alpha <\kappa $
and
![]() $i<\theta $
, let
$i<\theta $
, let
so that
![]() $\langle A^i_{\alpha }\mathrel {|} i<\theta \rangle $
is a
$\langle A^i_{\alpha }\mathrel {|} i<\theta \rangle $
is a
![]() $\subseteq $
-increasing sequence, converging to
$\subseteq $
-increasing sequence, converging to
![]() $\kappa \setminus (\alpha +1)$
. Since U is, in particular, a
$\kappa \setminus (\alpha +1)$
. Since U is, in particular, a
![]() $\theta $
-indecomposable ultrafilter over
$\theta $
-indecomposable ultrafilter over
![]() $\kappa $
, we may find some
$\kappa $
, we may find some
![]() $i_{\alpha }<\theta $
such that
$i_{\alpha }<\theta $
such that
![]() $A^{i_{\alpha }}_{\alpha }\in U$
.
$A^{i_{\alpha }}_{\alpha }\in U$
.
Next, using the pigeonhole principle, let us fix
![]() $H\in [\kappa ]^{\kappa }$
and
$H\in [\kappa ]^{\kappa }$
and
![]() $i<\theta $
such that
$i<\theta $
such that
![]() $i_{\alpha }=i$
for all
$i_{\alpha }=i$
for all
![]() $\alpha \in H$
. As U is closed under intersections of length
$\alpha \in H$
. As U is closed under intersections of length
![]() $\theta $
, for every
$\theta $
, for every
![]() $A\in [H]^{\theta }$
, we may let
$A\in [H]^{\theta }$
, we may let
![]() $\beta _A:=\min (\bigcap _{\alpha \in A}A^i_{\alpha })$
, so that
$\beta _A:=\min (\bigcap _{\alpha \in A}A^i_{\alpha })$
, so that
![]() $\sup _{\alpha \in A}c(\alpha ,\beta _A)\le i$
.
$\sup _{\alpha \in A}c(\alpha ,\beta _A)\le i$
.
By Lemma 2.4(2), fix
![]() $\beta \in H$
such that
$\beta \in H$
such that
![]() $\{c(\alpha , \beta ) \mathrel {|} \alpha \in H \cap \beta \}$
is unbounded in
$\{c(\alpha , \beta ) \mathrel {|} \alpha \in H \cap \beta \}$
is unbounded in
![]() $\theta $
. Now, pick
$\theta $
. Now, pick
![]() $A\in [H\cap \beta ]^{\theta }$
such that
$A\in [H\cap \beta ]^{\theta }$
such that
![]() $\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
$\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
![]() $\theta $
. If c were weakly subadditive, then we could pick
$\theta $
. If c were weakly subadditive, then we could pick
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $D^c_{\le i+1}(\beta _A)\cap \beta \subseteq D^c_{\le j}(\beta )$
. Then
$D^c_{\le i+1}(\beta _A)\cap \beta \subseteq D^c_{\le j}(\beta )$
. Then
![]() $A\subseteq D^c_{\le j}(\beta )$
, contradicting the choice of A.
$A\subseteq D^c_{\le j}(\beta )$
, contradicting the choice of A.
(2) Let H, i, and the notation
![]() $\beta _A$
be as in the proof of Clause (1). Assuming that
$\beta _A$
be as in the proof of Clause (1). Assuming that
![]() $\kappa $
is
$\kappa $
is
![]() $\theta $
-inaccessible, and using Lemma 2.4(1), we may find some
$\theta $
-inaccessible, and using Lemma 2.4(1), we may find some
![]() $A\in [H]^{\theta }$
such that, for cofinally many
$A\in [H]^{\theta }$
such that, for cofinally many
![]() $\beta <\kappa $
,
$\beta <\kappa $
,
![]() $\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
$\{c(\alpha , \beta ) \mathrel {|} \alpha \in A\}$
is unbounded in
![]() $\theta $
. In particular, we may find such a
$\theta $
. In particular, we may find such a
![]() $\beta <\kappa $
above
$\beta <\kappa $
above
![]() $\beta _A$
. If c were weakly subadditive of the first kind, then we could find
$\beta _A$
. If c were weakly subadditive of the first kind, then we could find
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $D_{\le i}^c(\beta _A)\subseteq D_{\le j}^c(\beta )$
. However, for every
$D_{\le i}^c(\beta _A)\subseteq D_{\le j}^c(\beta )$
. However, for every
![]() $j<\theta $
, there exists
$j<\theta $
, there exists
![]() $\alpha \in A$
such that
$\alpha \in A$
such that
![]() $c(\alpha ,\beta )>j$
, so that
$c(\alpha ,\beta )>j$
, so that
![]() $\alpha \in D_{\le i}^c(\beta _A)\setminus D_{\le j}^c(\beta )$
. This is a contradiction.
$\alpha \in D_{\le i}^c(\beta _A)\setminus D_{\le j}^c(\beta )$
. This is a contradiction.
(3) Suppose that U is a
![]() $\theta $
-indecomposable ultrafilter over
$\theta $
-indecomposable ultrafilter over
![]() $\kappa $
. As in the proof of Clause (1), we may fix
$\kappa $
. As in the proof of Clause (1), we may fix
![]() $H\in [\kappa ]^{\kappa }$
and
$H\in [\kappa ]^{\kappa }$
and
![]() $i<\theta $
such that, for all
$i<\theta $
such that, for all
![]() $\alpha \in H$
,
$\alpha \in H$
,
![]() $A^i_{\alpha }:=\{\beta <\kappa \mathrel {|} \alpha <\beta \ \&\ c(\alpha ,\beta )\le i\}$
is in U. Towards a contradiction, suppose that c is subadditive of the second kind. Then, for all
$A^i_{\alpha }:=\{\beta <\kappa \mathrel {|} \alpha <\beta \ \&\ c(\alpha ,\beta )\le i\}$
is in U. Towards a contradiction, suppose that c is subadditive of the second kind. Then, for all
![]() $(\alpha ,\beta )\in [H]^2$
, we may pick some
$(\alpha ,\beta )\in [H]^2$
, we may pick some
![]() $\gamma \in A^{i}_{\alpha }\cap A^i_{\beta }$
, and infer that
$\gamma \in A^{i}_{\alpha }\cap A^i_{\beta }$
, and infer that
![]() $c(\alpha ,\beta )\le \max \{c(\alpha ,\gamma ), c(\beta ,\gamma )\}\le i$
. So,
$c(\alpha ,\beta )\le \max \{c(\alpha ,\gamma ), c(\beta ,\gamma )\}\le i$
. So,
![]() $\sup (c"[H]^2)\le i$
, contradicting the fact that c witnesses
$\sup (c"[H]^2)\le i$
, contradicting the fact that c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
Corollary 3.39. Under a suitable large cardinal hypothesis, each of the following statements is consistent:
-
(1) For every
 $n<\omega $
, there is no weakly subadditive witness to
$n<\omega $
, there is no weakly subadditive witness to
 $\operatorname {\mathrm {U}}(\aleph _{\omega +1}, 2, \aleph _n,2)$
.
$\operatorname {\mathrm {U}}(\aleph _{\omega +1}, 2, \aleph _n,2)$
. -
(2) For every positive
 $n<\omega $
, there is no witness to
$n<\omega $
, there is no witness to
 $\operatorname {\mathrm {U}}(\aleph _{\omega +1},2,\aleph _n,2)$
that is subadditive of the second kind.
$\operatorname {\mathrm {U}}(\aleph _{\omega +1},2,\aleph _n,2)$
that is subadditive of the second kind.
Proof
-
(1) By [Reference Lambie-Hanson16, Corollary 5.13], relative to the consistency of the existence of infinitely many supercompact cardinals, it is consistent that, for every
 $n<\omega $
, any witness to
$n<\omega $
, any witness to
 $\operatorname {\mathrm {U}}(\aleph _{\omega +1},2, \aleph _n,2)$
is not subadditive. An inspection of [Reference Lambie-Hanson16, Lemma 5.11], on which [Reference Lambie-Hanson16, Corollary 5.13] relies, makes it clear that one obtains a model in which, furthermore, for every
$\operatorname {\mathrm {U}}(\aleph _{\omega +1},2, \aleph _n,2)$
is not subadditive. An inspection of [Reference Lambie-Hanson16, Lemma 5.11], on which [Reference Lambie-Hanson16, Corollary 5.13] relies, makes it clear that one obtains a model in which, furthermore, for every
 $n<\omega $
, any witness to
$n<\omega $
, any witness to
 $\operatorname {\mathrm {U}}(\aleph _{\omega +1},2, \aleph _n,2)$
is not weakly subadditive.
$\operatorname {\mathrm {U}}(\aleph _{\omega +1},2, \aleph _n,2)$
is not weakly subadditive. -
(3) Starting from the consistency of the existence of a cardinal
 $\kappa $
that is
$\kappa $
that is
 $\kappa ^+$
-supercompact, Ben-David and Magidor produced in [Reference Beaudoin2] a model of
$\kappa ^+$
-supercompact, Ben-David and Magidor produced in [Reference Beaudoin2] a model of
 $\textsf{ZFC}$
in which there exists an ultrafilter over
$\textsf{ZFC}$
in which there exists an ultrafilter over
 $\aleph _{\omega + 1}$
that is
$\aleph _{\omega + 1}$
that is
 $\aleph _{n}$
-indecomposable for all positive
$\aleph _{n}$
-indecomposable for all positive
 $n < \omega $
. Now appeal to Lemma 3.38.
$n < \omega $
. Now appeal to Lemma 3.38.
Lemma 3.40. Suppose that
![]() $\theta \le \mu <\kappa $
, and
$\theta \le \mu <\kappa $
, and
![]() $c:[\kappa ]^2\rightarrow \theta $
witnesses
$c:[\kappa ]^2\rightarrow \theta $
witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,\mu \circledast 1,\theta ,2)$
. If there exists a
$\operatorname {\mathrm {U}}(\kappa ,\mu \circledast 1,\theta ,2)$
. If there exists a
![]() $\mu ^+$
-complete uniform ultrafilter over
$\mu ^+$
-complete uniform ultrafilter over
![]() $\kappa $
, then c is not
$\kappa $
, then c is not
![]() $\mu $
-coherent.
$\mu $
-coherent.
Proof As in the proof of Lemma 3.38(1), a
![]() $\mu ^+$
-complete uniform ultrafilter over
$\mu ^+$
-complete uniform ultrafilter over
![]() $\kappa $
gives rise to
$\kappa $
gives rise to
![]() $H\in [\kappa ]^{\kappa }$
and
$H\in [\kappa ]^{\kappa }$
and
![]() $i<\theta $
such that, for every
$i<\theta $
such that, for every
![]() $A\in [H]^{\mu }$
, there exists
$A\in [H]^{\mu }$
, there exists
![]() $\beta _A<\kappa $
above
$\beta _A<\kappa $
above
![]() $\sup (A)$
such that
$\sup (A)$
such that
![]() $\sup _{\alpha \in A}c(\alpha ,\beta _A)\le i$
. Now, as c witnesses
$\sup _{\alpha \in A}c(\alpha ,\beta _A)\le i$
. Now, as c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa ,\mu \circledast 1,\theta ,2)$
, we may find
$\operatorname {\mathrm {U}}(\kappa ,\mu \circledast 1,\theta ,2)$
, we may find
![]() $A\in [H]^{\mu }$
and
$A\in [H]^{\mu }$
and
![]() $\beta \in H$
above
$\beta \in H$
above
![]() $\sup (A)$
such that
$\sup (A)$
such that
![]() $c(\alpha ,\beta )>i$
for all
$c(\alpha ,\beta )>i$
for all
![]() $\alpha \in A$
. So
$\alpha \in A$
. So
covers A, which is a set of size
![]() $\mu $
. Thereby, c is not
$\mu $
. Thereby, c is not
![]() $\mu $
-coherent.
$\mu $
-coherent.
Corollary 3.41 (Todorcevic [Reference Todorcevic34, Remark 6.2.3]).
Suppose that
![]() $\lambda $
is a singular limit of strongly compact cardinals. Then there exists no locally small coloring
$\lambda $
is a singular limit of strongly compact cardinals. Then there exists no locally small coloring
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
that is
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
that is
![]() $\lambda $
-coherent.
$\lambda $
-coherent.
Proof Fix a strictly increasing sequence of strongly compact cardinals
![]() $\langle \lambda _i\mathrel {|} i<\operatorname {\mathrm {cf}}(\lambda )\rangle $
converging to
$\langle \lambda _i\mathrel {|} i<\operatorname {\mathrm {cf}}(\lambda )\rangle $
converging to
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
be a locally small coloring. Towards a contradiction, suppose that c is
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
be a locally small coloring. Towards a contradiction, suppose that c is
![]() $\lambda $
-coherent, and then define
$\lambda $
-coherent, and then define
![]() $d:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
via
$d:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
via
It is not hard to see that d is subadditive, and so, by Lemma 3.38(3), d fails to witness
![]() $\operatorname {\mathrm {U}}(\lambda ^+,2,\operatorname {\mathrm {cf}}(\lambda ),2)$
. This means that there exist
$\operatorname {\mathrm {U}}(\lambda ^+,2,\operatorname {\mathrm {cf}}(\lambda ),2)$
. This means that there exist
![]() $H\in [\lambda ^+]^{\lambda ^+}$
and
$H\in [\lambda ^+]^{\lambda ^+}$
and
![]() $i<\operatorname {\mathrm {cf}}(\lambda )$
such that
$i<\operatorname {\mathrm {cf}}(\lambda )$
such that
![]() $d"[H]^2\subseteq i$
. Define
$d"[H]^2\subseteq i$
. Define
![]() $e:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
via
$e:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
via
![]() $e(\alpha ,\beta ):=c(\alpha ,\min (H\setminus \beta ))$
. Then e is a locally small coloring which is moreover
$e(\alpha ,\beta ):=c(\alpha ,\min (H\setminus \beta ))$
. Then e is a locally small coloring which is moreover
![]() $\lambda _i$
-coherent. By Lemma 3.12(1), e in particular witnesses
$\lambda _i$
-coherent. By Lemma 3.12(1), e in particular witnesses
![]() $\operatorname {\mathrm {U}}(\lambda ^+,\lambda _{i}\circledast 1,\operatorname {\mathrm {cf}}(\lambda ),2)$
, and then Lemma 3.40 implies that there exists no
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda _{i}\circledast 1,\operatorname {\mathrm {cf}}(\lambda ),2)$
, and then Lemma 3.40 implies that there exists no
![]() $(\lambda _{i})^+$
-complete uniform ultrafilter over
$(\lambda _{i})^+$
-complete uniform ultrafilter over
![]() $\lambda ^+$
, contradicting the facts that
$\lambda ^+$
, contradicting the facts that
![]() $\lambda _i<\lambda _{i+1}<\lambda ^+$
and
$\lambda _i<\lambda _{i+1}<\lambda ^+$
and
![]() $\lambda _{i+1}$
is strongly compact.
$\lambda _{i+1}$
is strongly compact.
Complementary to Lemma 3.13, we obtain the following.
Corollary 3.42. Suppose that
![]() $c:[\kappa ]^2\rightarrow \theta $
is a witness to
$c:[\kappa ]^2\rightarrow \theta $
is a witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
and there exists a strongly compact cardinal in the interval
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
and there exists a strongly compact cardinal in the interval
![]() $(\theta ,\kappa ]$
.
$(\theta ,\kappa ]$
.
-
(1) c is not weakly subadditive.
-
(2) If
 $\kappa $
is not the successor of a singular cardinal of cofinality
$\kappa $
is not the successor of a singular cardinal of cofinality
 $\theta $
, then c is not weakly subadditive of the first kind.
$\theta $
, then c is not weakly subadditive of the first kind. -
(3) c is not subadditive of the second kind.
Proof The hypothesis entails the existence of a
![]() $\theta ^+$
-complete uniform ultrafilter over
$\theta ^+$
-complete uniform ultrafilter over
![]() $\kappa $
, and in particular, the existence of a
$\kappa $
, and in particular, the existence of a
![]() $\theta $
-indecomposable uniform ultrafilter over
$\theta $
-indecomposable uniform ultrafilter over
![]() $\kappa $
. In addition, if
$\kappa $
. In addition, if
![]() $\kappa $
is not the successor of a singular cardinal of cofinality
$\kappa $
is not the successor of a singular cardinal of cofinality
![]() $\theta $
, then by Solovay’s theorem stating that
$\theta $
, then by Solovay’s theorem stating that
![]() $\textsf {SCH}$
holds above a strongly compact cardinal [Reference Solovay, Henkin, Addison, Chang, Craig, Scott and Vaught31],
$\textsf {SCH}$
holds above a strongly compact cardinal [Reference Solovay, Henkin, Addison, Chang, Craig, Scott and Vaught31],
![]() $\kappa $
is
$\kappa $
is
![]() $\theta $
-inaccessible. Now appeal to Lemma 3.38.
$\theta $
-inaccessible. Now appeal to Lemma 3.38.
Remark 3.43. A similar statement can consistently hold at small cardinals. By [Reference Lücke24, Lemma 3.2(v)] and Lemma 3.5, if
![]() $\kappa $
is weakly compact and
$\kappa $
is weakly compact and
![]() $\lambda <\kappa $
is any regular uncountable cardinal, then in the forcing extension by
$\lambda <\kappa $
is any regular uncountable cardinal, then in the forcing extension by
![]() $\mathrm {Coll}(\lambda ,{<}\kappa )$
, for every
$\mathrm {Coll}(\lambda ,{<}\kappa )$
, for every
![]() $\theta <\lambda $
,
$\theta <\lambda $
,
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, 2, \theta , 2)$
fails.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, 2, \theta , 2)$
fails.
Lemma 3.14(1) implies that the restriction “
![]() $\theta <\lambda $
” in the preceding remark cannot be waived.
$\theta <\lambda $
” in the preceding remark cannot be waived.
Corollary 3.44. It is consistent that all of the following hold simultaneously:
-
•
 $\textsf{GCH}$
;
$\textsf{GCH}$
; -
•
 $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\omega _2,\omega _2,\omega _1,\omega _1)$
holds
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\omega _2,\omega _2,\omega _1,\omega _1)$
holds
 $;$
$;$
-
•
 $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\omega _2,2,\omega ,2)$
fails.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\omega _2,2,\omega ,2)$
fails.
In [Reference Viale35, Definition 8], Viale defined the covering property
![]() $\operatorname {\mathrm {CP}}(\kappa ,\theta )$
. In [Reference Lambie-Hanson16, Lemma 5.11], the first author proved that for infinite regular cardinals
$\operatorname {\mathrm {CP}}(\kappa ,\theta )$
. In [Reference Lambie-Hanson16, Lemma 5.11], the first author proved that for infinite regular cardinals
![]() $\theta <\kappa $
,
$\theta <\kappa $
,
![]() $\operatorname {\mathrm {CP}}(\kappa ,\theta )$
implies that
$\operatorname {\mathrm {CP}}(\kappa ,\theta )$
implies that
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
fails. By [Reference Viale35, Section 6], the P-ideal dichotomy (
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
fails. By [Reference Viale35, Section 6], the P-ideal dichotomy (
![]() $\textsf {PID}$
), which is a consequence of the proper forcing axiom (
$\textsf {PID}$
), which is a consequence of the proper forcing axiom (
![]() $\textsf {PFA}$
), implies that
$\textsf {PFA}$
), implies that
![]() $\operatorname {\mathrm {CP}}(\kappa ,\omega )$
holds for every regular
$\operatorname {\mathrm {CP}}(\kappa ,\omega )$
holds for every regular
![]() $\kappa \geq \aleph _2$
(the relevant result in [Reference Viale35] is only stated for
$\kappa \geq \aleph _2$
(the relevant result in [Reference Viale35] is only stated for
![]() $\kappa> \mathfrak {c}$
, but its proof works without any modifications for any regular
$\kappa> \mathfrak {c}$
, but its proof works without any modifications for any regular
![]() $\kappa \geq \aleph _2$
). Putting this all together, we see that the failure of
$\kappa \geq \aleph _2$
). Putting this all together, we see that the failure of
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\omega ,2)$
for all regular
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\omega ,2)$
for all regular
![]() $\kappa \geq \aleph _2$
already follows from
$\kappa \geq \aleph _2$
already follows from
![]() $\textsf {PID}$
.
$\textsf {PID}$
.
Here, by combining the arguments of [Reference Todorcevic34, Section 7], [Reference Viale35, Section 6], and [Reference Lambie-Hanson16, Section 5], we provide a self-contained proof of a slightly more informative result:
Theorem 3.45 (Todorcevic and Viale).
Suppose that
![]() $\textsf {PID}$
holds and
$\textsf {PID}$
holds and
![]() $c:[\kappa ]^2\rightarrow \omega $
witnesses
$c:[\kappa ]^2\rightarrow \omega $
witnesses
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \omega , 2)$
.
$\operatorname {\mathrm {U}}(\kappa , 2, \omega , 2)$
.
-
(1) If
 $\kappa \ge \aleph _2$
, then c is not weakly subadditive.
$\kappa \ge \aleph _2$
, then c is not weakly subadditive. -
(2) If
 $\kappa>2^{\aleph _0}$
is not the successor of a singular cardinal of countable cofinality, then c is not weakly subadditive of the first kind.
$\kappa>2^{\aleph _0}$
is not the successor of a singular cardinal of countable cofinality, then c is not weakly subadditive of the first kind.
Proof Suppose not. For all
![]() $X\in [\kappa ]^{\le \aleph _0}$
and
$X\in [\kappa ]^{\le \aleph _0}$
and
![]() $\beta <\kappa $
, define a function
$\beta <\kappa $
, define a function
![]() $f^{\beta }_X:X\cap \beta \rightarrow \omega $
by letting
$f^{\beta }_X:X\cap \beta \rightarrow \omega $
by letting
![]() $f^{\beta }_X(\alpha ):=c(\alpha ,\beta )$
. Note that if
$f^{\beta }_X(\alpha ):=c(\alpha ,\beta )$
. Note that if
![]() $\kappa>2^{\aleph _0}$
, then for every
$\kappa>2^{\aleph _0}$
, then for every
![]() $X\in [\kappa ]^{\le \aleph _0}$
, there exists some
$X\in [\kappa ]^{\le \aleph _0}$
, there exists some
![]() $\Gamma \in [\kappa ]^{\kappa }$
such that
$\Gamma \in [\kappa ]^{\kappa }$
such that
![]() $f^{\gamma }_X=f^{\delta }_X$
for all
$f^{\gamma }_X=f^{\delta }_X$
for all
![]() $(\gamma ,\delta )\in [\Gamma ]^2$
. In this case, we shall denote such a set
$(\gamma ,\delta )\in [\Gamma ]^2$
. In this case, we shall denote such a set
![]() $\Gamma $
by
$\Gamma $
by
![]() $\Gamma _X$
and
$\Gamma _X$
and
![]() $\min (\Gamma _X)$
by
$\min (\Gamma _X)$
by
![]() $\gamma _X$
.
$\gamma _X$
.
Now, let
![]() $\mathcal I$
be the collection of all
$\mathcal I$
be the collection of all
![]() $X\in [\kappa ]^{\le \aleph _0}$
such that, for every
$X\in [\kappa ]^{\le \aleph _0}$
such that, for every
![]() $\beta <\kappa $
,
$\beta <\kappa $
,
![]() $f^{\beta }_X$
is finite-to-one. It is clear that
$f^{\beta }_X$
is finite-to-one. It is clear that
![]() $\mathcal I$
is an ideal.
$\mathcal I$
is an ideal.
Claim 3.45.1. Let
![]() $Z\in [\kappa ]^{<\kappa }$
. Then there exists an ordinal
$Z\in [\kappa ]^{<\kappa }$
. Then there exists an ordinal
![]() $\epsilon _Z\in [\operatorname {\mathrm {ssup}}(Z),\kappa )$
such that, for every
$\epsilon _Z\in [\operatorname {\mathrm {ssup}}(Z),\kappa )$
such that, for every
![]() $X\in [Z]^{\le \aleph _0}$
,
$X\in [Z]^{\le \aleph _0}$
,
![]() $X\in \mathcal I$
iff there exists
$X\in \mathcal I$
iff there exists
![]() $\gamma \in [\epsilon _Z,\kappa )$
for which
$\gamma \in [\epsilon _Z,\kappa )$
for which
![]() $f^{\gamma }_X$
is finite-to-one.
$f^{\gamma }_X$
is finite-to-one.
Proof
![]() $\blacktriangleright $
If c is weakly subadditive, then set
$\blacktriangleright $
If c is weakly subadditive, then set
![]() $\epsilon _Z:=\operatorname {\mathrm {ssup}}(Z)$
. Towards a contradiction, suppose that there exist
$\epsilon _Z:=\operatorname {\mathrm {ssup}}(Z)$
. Towards a contradiction, suppose that there exist
![]() $X\in [Z]^{\le \aleph _0}$
and
$X\in [Z]^{\le \aleph _0}$
and
![]() $\gamma \in [\epsilon _Z,\kappa )$
such that
$\gamma \in [\epsilon _Z,\kappa )$
such that
![]() $f^{\gamma }_X$
is finite-to-one, yet
$f^{\gamma }_X$
is finite-to-one, yet
![]() $X\not \in \mathcal I$
. Fix
$X\not \in \mathcal I$
. Fix
![]() $\beta <\kappa $
such that
$\beta <\kappa $
such that
![]() $f^{\beta }_X$
is not finite-to-one, and then fix
$f^{\beta }_X$
is not finite-to-one, and then fix
![]() $i<\omega $
for which
$i<\omega $
for which
![]() $Y:=X\cap D^c_{\le i}(\beta )$
is infinite. Find
$Y:=X\cap D^c_{\le i}(\beta )$
is infinite. Find
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $D^c_{\le i}(\beta )\cap \gamma \subseteq D^c_{\le j}(\gamma )$
. Then
$D^c_{\le i}(\beta )\cap \gamma \subseteq D^c_{\le j}(\gamma )$
. Then
![]() $X\cap D^c_{\le j}(\gamma )$
covers the infinite set Y, contradicting the fact that
$X\cap D^c_{\le j}(\gamma )$
covers the infinite set Y, contradicting the fact that
![]() $f_X^{\gamma }$
is finite-to-one.
$f_X^{\gamma }$
is finite-to-one.
![]() $\blacktriangleright $
If
$\blacktriangleright $
If
![]() $\kappa>2^{\aleph _0}$
is not the successor of a singular cardinal of countable cofinality, then by Viale’s theorem [Reference Viale35] stating that
$\kappa>2^{\aleph _0}$
is not the successor of a singular cardinal of countable cofinality, then by Viale’s theorem [Reference Viale35] stating that
![]() $\textsf {PID}$
implies
$\textsf {PID}$
implies
![]() $\textsf {SCH}$
, the fact that
$\textsf {SCH}$
, the fact that
![]() $|Z|<\kappa $
implies that
$|Z|<\kappa $
implies that
![]() $|Z|^{\aleph _0}<\kappa $
. It follows that
$|Z|^{\aleph _0}<\kappa $
. It follows that
![]() $\epsilon _Z:=\sup \{\gamma _X\mathrel {|} X\in [Z]^{\le \aleph _0}\}+1$
is
$\epsilon _Z:=\sup \{\gamma _X\mathrel {|} X\in [Z]^{\le \aleph _0}\}+1$
is
![]() $<\kappa $
. Suppose that c is weakly subadditive of the first kind; yet, there exist
$<\kappa $
. Suppose that c is weakly subadditive of the first kind; yet, there exist
![]() $X\in [Z]^{\le \aleph _0}\setminus \mathcal I$
and
$X\in [Z]^{\le \aleph _0}\setminus \mathcal I$
and
![]() $\gamma \in [\epsilon _Z,\kappa )$
such that
$\gamma \in [\epsilon _Z,\kappa )$
such that
![]() $f^{\gamma }_X$
is finite-to-one. Fix
$f^{\gamma }_X$
is finite-to-one. Fix
![]() $\beta <\kappa $
and
$\beta <\kappa $
and
![]() $i<\omega $
such that
$i<\omega $
such that
![]() $Y:=X\cap D^c_{\le i}(\beta )$
is infinite. Pick
$Y:=X\cap D^c_{\le i}(\beta )$
is infinite. Pick
![]() $\delta \in \Gamma _X$
above
$\delta \in \Gamma _X$
above
![]() $\beta $
, and use weak subadditivity of the first kind to find
$\beta $
, and use weak subadditivity of the first kind to find
![]() $j<\theta $
such that
$j<\theta $
such that
![]() $D^c_{\le i}(\beta )\subseteq D^c_{\le j}(\delta )$
. As
$D^c_{\le i}(\beta )\subseteq D^c_{\le j}(\delta )$
. As
![]() $\delta \in \Gamma _X$
,
$\delta \in \Gamma _X$
,
![]() $X\cap D^c_{\le j}(\delta )=X\cap D^c_{\le j}(\gamma _X)$
, so that
$X\cap D^c_{\le j}(\delta )=X\cap D^c_{\le j}(\gamma _X)$
, so that
![]() $Y\subseteq D^c_{\le j}(\gamma _X)$
. As
$Y\subseteq D^c_{\le j}(\gamma _X)$
. As
![]() $\gamma _X<\epsilon _Z\le \gamma $
, we use weak subadditivity of the first kind to find
$\gamma _X<\epsilon _Z\le \gamma $
, we use weak subadditivity of the first kind to find
![]() $k<\theta $
such that
$k<\theta $
such that
![]() $D^c_{\le j}(\gamma _X)\subseteq D^c_{\le k}(\gamma )$
. Altogether,
$D^c_{\le j}(\gamma _X)\subseteq D^c_{\le k}(\gamma )$
. Altogether,
![]() $Y\subseteq D^c_{\le k}(\gamma )$
, so that
$Y\subseteq D^c_{\le k}(\gamma )$
, so that
![]() $f_X^{\gamma }[Y]\subseteq k+1$
, contradicting the fact that
$f_X^{\gamma }[Y]\subseteq k+1$
, contradicting the fact that
![]() $f^{\gamma }_X$
is finite-to-one.
$f^{\gamma }_X$
is finite-to-one.
To see that
![]() $\mathcal I$
is a P-ideal, suppose that
$\mathcal I$
is a P-ideal, suppose that
![]() $\vec X=\langle X_n\mathrel {|} n<\omega \rangle $
is a sequence of sets in
$\vec X=\langle X_n\mathrel {|} n<\omega \rangle $
is a sequence of sets in
![]() $\mathcal I$
. Set
$\mathcal I$
. Set
![]() $\gamma :=\epsilon _Z$
, for
$\gamma :=\epsilon _Z$
, for
![]() $Z:=\bigcup _{n<\omega }X_n$
. Evidently
$Z:=\bigcup _{n<\omega }X_n$
. Evidently
![]() $Y:=\bigcup _{n<\omega }(X_n\setminus D^c_{\le n}(\gamma ))$
is a pseudo-union for
$Y:=\bigcup _{n<\omega }(X_n\setminus D^c_{\le n}(\gamma ))$
is a pseudo-union for
![]() $\vec X$
. In addition, for every
$\vec X$
. In addition, for every
![]() $i<\omega $
,
$i<\omega $
,
![]() $Y\cap D^c_{\le i}(\gamma )$
is covered by the finite set
$Y\cap D^c_{\le i}(\gamma )$
is covered by the finite set
![]() $\bigcup _{n<i}(X_n\cap D^c_{\le i}(\gamma ))$
, so, by the preceding claim,
$\bigcup _{n<i}(X_n\cap D^c_{\le i}(\gamma ))$
, so, by the preceding claim,
![]() $Y\in \mathcal I$
.
$Y\in \mathcal I$
.
Finally, by
![]() $\textsf {PID}$
, one of the following alternatives must hold:
$\textsf {PID}$
, one of the following alternatives must hold:
-
(1) There exists
 $A\in [\kappa ]^{\kappa }$
such that
$A\in [\kappa ]^{\kappa }$
such that
 $[A]^{\aleph _0}\cap \mathcal I=\emptyset $
.
$[A]^{\aleph _0}\cap \mathcal I=\emptyset $
. -
(2) There exists
 $B\in [\kappa ]^{\aleph _1}$
such that
$B\in [\kappa ]^{\aleph _1}$
such that
 $[B]^{\aleph _0}\subseteq \mathcal I$
.
$[B]^{\aleph _0}\subseteq \mathcal I$
.
In Case (1), given
![]() $A\in [\kappa ]^{\kappa }$
, pick some strictly increasing function
$A\in [\kappa ]^{\kappa }$
, pick some strictly increasing function
![]() $g:\kappa \rightarrow A$
such that
$g:\kappa \rightarrow A$
such that
![]() $g(\alpha )>\epsilon _{A\cap \operatorname {\mathrm {ssup}}(g[\alpha ])}$
for all
$g(\alpha )>\epsilon _{A\cap \operatorname {\mathrm {ssup}}(g[\alpha ])}$
for all
![]() $\alpha <\kappa $
. It follows that
$\alpha <\kappa $
. It follows that
![]() $A':=\operatorname {\mathrm {Im}}(g)$
is a cofinal subset of A such that
$A':=\operatorname {\mathrm {Im}}(g)$
is a cofinal subset of A such that
![]() $\epsilon _{A'\cap \gamma }<\gamma $
for every
$\epsilon _{A'\cap \gamma }<\gamma $
for every
![]() $\gamma \in A'$
. Next, by Lemma 2.4(2), we may fix
$\gamma \in A'$
. Next, by Lemma 2.4(2), we may fix
![]() $\gamma \in A'$
such that
$\gamma \in A'$
such that
![]() $\{c(\alpha , \gamma ) \mathrel {|} \alpha \in A' \cap \gamma \}$
is infinite. So, we may find
$\{c(\alpha , \gamma ) \mathrel {|} \alpha \in A' \cap \gamma \}$
is infinite. So, we may find
![]() $X\in [A'\cap \gamma ]^{\aleph _0}$
such that
$X\in [A'\cap \gamma ]^{\aleph _0}$
such that
![]() $f^{\gamma }_X$
is one-to-one. As
$f^{\gamma }_X$
is one-to-one. As
![]() $\epsilon _{A'\cap \gamma }<\gamma $
, the preceding claim implies that
$\epsilon _{A'\cap \gamma }<\gamma $
, the preceding claim implies that
![]() $X\in \mathcal I$
. In particular,
$X\in \mathcal I$
. In particular,
![]() $[A]^{\aleph _0}\cap \mathcal I\neq \emptyset $
.
$[A]^{\aleph _0}\cap \mathcal I\neq \emptyset $
.
In Case (2), given
![]() $B\in [\kappa ]^{\aleph _1}$
, let
$B\in [\kappa ]^{\aleph _1}$
, let
![]() $\beta :=\operatorname {\mathrm {ssup}}(B)$
. As
$\beta :=\operatorname {\mathrm {ssup}}(B)$
. As
![]() $B\cap \bigcup _{i<\omega }D^c_{\le i}(\beta )$
is uncountable, we may find some
$B\cap \bigcup _{i<\omega }D^c_{\le i}(\beta )$
is uncountable, we may find some
![]() $i<\omega $
such that
$i<\omega $
such that
![]() $B\cap D^c_{\le i}(\beta )$
is uncountable. In particular, there exist
$B\cap D^c_{\le i}(\beta )$
is uncountable. In particular, there exist
![]() $X\in [B]^{\aleph _0}$
such that
$X\in [B]^{\aleph _0}$
such that
![]() $X\cap D^c_{\le i}(\beta )$
is infinite. So,
$X\cap D^c_{\le i}(\beta )$
is infinite. So,
![]() $[B]^{\aleph _0}\nsubseteq \mathcal I$
.
$[B]^{\aleph _0}\nsubseteq \mathcal I$
.
On the other hand, since
![]() $\textsf {MM}$
is preserved by
$\textsf {MM}$
is preserved by
![]() $\omega _2$
-directed closed set forcings, Theorem 3.34 implies that
$\omega _2$
-directed closed set forcings, Theorem 3.34 implies that
![]() $\textsf {MM}$
does not refute
$\textsf {MM}$
does not refute
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa , \theta , \theta )$
for regular uncountable cardinals
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa , \theta , \theta )$
for regular uncountable cardinals
![]() $\theta <\kappa $
.
$\theta <\kappa $
.
Corollary 3.46. In the model of [Reference Todorčević33], for every regular uncountable cardinal
![]() $\kappa $
, the following are equivalent:
$\kappa $
, the following are equivalent:
-
• There is a witness to
 $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\omega ,\omega )$
that is subadditive of the first kind.
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\omega ,\omega )$
that is subadditive of the first kind. -
• There is a witness to
 $\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
that is weakly subadditive of the first kind.
$\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
that is weakly subadditive of the first kind. -
•
 $\kappa $
is the successor of a cardinal of countable cofinality.
$\kappa $
is the successor of a cardinal of countable cofinality.
Proof By Lemma 3.13, if
![]() $\kappa =\lambda ^+$
for an infinite cardinal
$\kappa =\lambda ^+$
for an infinite cardinal
![]() $\lambda $
of countable cofinality, then there exists a witness to
$\lambda $
of countable cofinality, then there exists a witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\omega ,\omega )$
that is subadditive of the first kind. For any other
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\omega ,\omega )$
that is subadditive of the first kind. For any other
![]() $\kappa $
, since in the model of [Reference Todorčević33],
$\kappa $
, since in the model of [Reference Todorčević33],
![]() $\textsf {CH}$
and
$\textsf {CH}$
and
![]() $\textsf {PID}$
both hold, Theorem 3.45(2) implies that no witness to
$\textsf {PID}$
both hold, Theorem 3.45(2) implies that no witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
is weakly subadditive of the first kind.
$\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
is weakly subadditive of the first kind.
We conclude this section by pointing out a corollary to Theorem 3.45 and the arguments from the proofs of Lemma 3.33 and Corollary 3.41.
Corollary 3.47. Assuming
![]() $\textsf {PID}$
, for every singular cardinal
$\textsf {PID}$
, for every singular cardinal
![]() $\lambda $
of countable cofinality, every locally small coloring
$\lambda $
of countable cofinality, every locally small coloring
![]() $c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
that is subadditive of the first kind is not
$c:[\lambda ^+]^2\rightarrow \operatorname {\mathrm {cf}}(\lambda )$
that is subadditive of the first kind is not
![]() $\lambda $
-coherent.
$\lambda $
-coherent.
4 Indexed square sequences
Recall that the principle
![]() $\square (\kappa ,\theta ,{\sqsubseteq _{\chi }})$
asserts the existence of a sequence
$\square (\kappa ,\theta ,{\sqsubseteq _{\chi }})$
asserts the existence of a sequence
![]() $\langle \mathcal C_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
satisfying all of the following:
$\langle \mathcal C_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
satisfying all of the following:
-
• For every limit ordinal
 $\alpha <\kappa $
,
$\alpha <\kappa $
,
 $\mathcal C_{\alpha }$
is a collection of clubs in
$\mathcal C_{\alpha }$
is a collection of clubs in
 $\alpha $
, and
$\alpha $
, and
 $1\le |\mathcal C_{\alpha }|\le \theta $
.
$1\le |\mathcal C_{\alpha }|\le \theta $
. -
• For all
 $\alpha <\kappa $
,
$\alpha <\kappa $
,
 $C\in \mathcal C_{\alpha }$
and
$C\in \mathcal C_{\alpha }$
and
 $\bar \alpha \in \operatorname {\mathrm {acc}}(C)$
, if
$\bar \alpha \in \operatorname {\mathrm {acc}}(C)$
, if
 $\operatorname {\mathrm {otp}}(C)\ge \chi $
, then
$\operatorname {\mathrm {otp}}(C)\ge \chi $
, then
 $C\cap \bar \alpha \in \mathcal C_{\bar \alpha }$
.
$C\cap \bar \alpha \in \mathcal C_{\bar \alpha }$
. -
• For every club D in
 $\kappa $
, there exists some
$\kappa $
, there exists some
 $\alpha \in \operatorname {\mathrm {acc}}(D)$
such that
$\alpha \in \operatorname {\mathrm {acc}}(D)$
such that
 $D\cap \alpha \notin \mathcal C_{\alpha }$
.
$D\cap \alpha \notin \mathcal C_{\alpha }$
.
Convention 4.1. If we omit
![]() $\theta $
, then we mean that
$\theta $
, then we mean that
![]() $\theta =1$
. If we omit
$\theta =1$
. If we omit
![]() $\sqsubseteq _{\chi }$
, then we mean that
$\sqsubseteq _{\chi }$
, then we mean that
![]() $\chi =\omega $
.
$\chi =\omega $
.
A strengthening of
![]() $\square (\kappa ,\theta )$
, denoted by
$\square (\kappa ,\theta )$
, denoted by
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
, was introduced in [Reference Lambie-Hanson17]. In this section, we identify a weakening of
$\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
, was introduced in [Reference Lambie-Hanson17]. In this section, we identify a weakening of
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
, denoted by
$\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
, denoted by
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
, that is tightly related to the existence of closed, subadditive witnesses to
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
, that is tightly related to the existence of closed, subadditive witnesses to
![]() $\operatorname {\mathrm {U}}(\kappa ,\ldots )$
.
$\operatorname {\mathrm {U}}(\kappa ,\ldots )$
.
Definition 4.2.
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
asserts the existence of a matrix
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
asserts the existence of a matrix
satisfying the following statements.
-
(1)
 $(E^{\kappa }_{\neq \theta } \cap \operatorname {\mathrm {acc}}(\kappa )) \subseteq \Gamma \subseteq \operatorname {\mathrm {acc}}(\kappa )$
.
$(E^{\kappa }_{\neq \theta } \cap \operatorname {\mathrm {acc}}(\kappa )) \subseteq \Gamma \subseteq \operatorname {\mathrm {acc}}(\kappa )$
. -
(2) For all
 $\alpha \in \Gamma $
, we have
$\alpha \in \Gamma $
, we have
 $i(\alpha ) < \theta $
, and
$i(\alpha ) < \theta $
, and
 $\langle C_{\alpha ,i}\mathrel {|} i(\alpha ) \leq i<\theta \rangle $
is a
$\langle C_{\alpha ,i}\mathrel {|} i(\alpha ) \leq i<\theta \rangle $
is a
 $\subseteq $
-increasing sequence of clubs in
$\subseteq $
-increasing sequence of clubs in
 $\alpha $
, with
$\alpha $
, with
 $\Gamma \cap \alpha = \bigcup _{i(\alpha )\le i<\theta }\operatorname {\mathrm {acc}}(C_{\alpha ,i})$
.
$\Gamma \cap \alpha = \bigcup _{i(\alpha )\le i<\theta }\operatorname {\mathrm {acc}}(C_{\alpha ,i})$
. -
(3) For all
 $\alpha \in \Gamma $
,
$\alpha \in \Gamma $
,
 $i(\alpha ) \leq i<\theta $
, and
$i(\alpha ) \leq i<\theta $
, and
 $\bar \alpha \in \operatorname {\mathrm {acc}}(C_{\alpha ,i})$
, we have
$\bar \alpha \in \operatorname {\mathrm {acc}}(C_{\alpha ,i})$
, we have
 $i(\bar \alpha ) \leq i$
and
$i(\bar \alpha ) \leq i$
and
 $C_{\bar \alpha ,i}=C_{\alpha ,i} \cap \bar \alpha $
.
$C_{\bar \alpha ,i}=C_{\alpha ,i} \cap \bar \alpha $
. -
(4) For every club D in
 $\kappa $
, there exists
$\kappa $
, there exists
 $\alpha \in \operatorname {\mathrm {acc}}(D) \cap \Gamma $
such that, for all
$\alpha \in \operatorname {\mathrm {acc}}(D) \cap \Gamma $
such that, for all
 $i<\theta $
,
$i<\theta $
,
 $D\cap \alpha \neq C_{\alpha ,i}$
.
$D\cap \alpha \neq C_{\alpha ,i}$
.
Remark 4.3. The principle
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
is the strengthening of
$\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
is the strengthening of
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
obtained by requiring that
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
obtained by requiring that
![]() $\Gamma = \operatorname {\mathrm {acc}}(\kappa )$
.
$\Gamma = \operatorname {\mathrm {acc}}(\kappa )$
.
We now turn to prove Theorem A.
Theorem 4.4. Suppose that
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. Then the following are equivalent.
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. Then the following are equivalent.
-
(1)
 $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds.
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds. -
(2) There exists a closed, subadditive witness to
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. -
(3) There exists a closed, subadditive witness to
 $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\sup (\operatorname {\mathrm {Reg}}(\kappa ))$
.
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,\sup (\operatorname {\mathrm {Reg}}(\kappa ))$
. -
(4) For every stationary
 $S\subseteq \kappa $
, there exists a
$S\subseteq \kappa $
, there exists a
 $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence
 $\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , i(\alpha ) \leq i < \theta \rangle $
such that either
$\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , i(\alpha ) \leq i < \theta \rangle $
such that either
 $S\cap \Gamma $
is nonstationary or, for all
$S\cap \Gamma $
is nonstationary or, for all
 $i < \theta $
,
$i < \theta $
,
 $\{\alpha \in S\cap \Gamma \mathrel {|} i(\alpha )> i\}$
is stationary.
$\{\alpha \in S\cap \Gamma \mathrel {|} i(\alpha )> i\}$
is stationary.
Proof
![]() $(2)\iff (3)$
By Lemma 3.2(3).
$(2)\iff (3)$
By Lemma 3.2(3).
![]() $(4)\implies (1)$
This is trivial.
$(4)\implies (1)$
This is trivial.
![]() $(1)\implies (2)$
: Fix a
$(1)\implies (2)$
: Fix a
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
-sequence,
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
-sequence,
![]() $\vec {C} = \langle C_{\alpha ,i}\mathrel {|} \alpha \in \Gamma , ~ i(\alpha ) \leq i<\theta \rangle $
. For each
$\vec {C} = \langle C_{\alpha ,i}\mathrel {|} \alpha \in \Gamma , ~ i(\alpha ) \leq i<\theta \rangle $
. For each
![]() $\alpha \in \kappa $
, let
$\alpha \in \kappa $
, let
![]() $\tilde {\alpha } := \min (\Gamma \setminus \alpha )$
. Define
$\tilde {\alpha } := \min (\Gamma \setminus \alpha )$
. Define
![]() $c:[\kappa ]^2 \rightarrow \theta $
by setting, for all
$c:[\kappa ]^2 \rightarrow \theta $
by setting, for all
![]() $(\alpha , \beta ) \in [\kappa ]^2$
,
$(\alpha , \beta ) \in [\kappa ]^2$
,
 $$ \begin{align*}c(\alpha, \beta) := \begin{cases} \min\{i \in [i(\tilde{\beta}), \theta) \mathrel{|} \tilde{\alpha} \in \operatorname{\mathrm{acc}}(C_{\tilde{\beta}, i})\}, & \text{if } \tilde{\alpha} < \tilde{\beta}, \\ 0, & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}c(\alpha, \beta) := \begin{cases} \min\{i \in [i(\tilde{\beta}), \theta) \mathrel{|} \tilde{\alpha} \in \operatorname{\mathrm{acc}}(C_{\tilde{\beta}, i})\}, & \text{if } \tilde{\alpha} < \tilde{\beta}, \\ 0, & \text{otherwise}. \end{cases} \end{align*} $$
Claim 4.4.1. c is closed.
Proof Fix
![]() $\beta < \kappa $
,
$\beta < \kappa $
,
![]() $i < \theta $
, and
$i < \theta $
, and
![]() $A \subseteq D^c_{\leq i}(\beta )$
with
$A \subseteq D^c_{\leq i}(\beta )$
with
![]() $\gamma : = \sup (A)$
in
$\gamma : = \sup (A)$
in
![]() $\beta \setminus A$
. To show that
$\beta \setminus A$
. To show that
![]() $\gamma \in D^c_{\leq i}(\beta )$
, there are two cases to consider.
$\gamma \in D^c_{\leq i}(\beta )$
, there are two cases to consider.
-
▸ If
 $\tilde {\alpha } < \gamma $
for all
$\tilde {\alpha } < \gamma $
for all
 $\alpha \in A$
, then, by our definition of c, it follows that
$\alpha \in A$
, then, by our definition of c, it follows that
 $\gamma \in \operatorname {\mathrm {acc}}(C_{\tilde {\beta }, i})$
, and hence
$\gamma \in \operatorname {\mathrm {acc}}(C_{\tilde {\beta }, i})$
, and hence
 $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
 $\gamma = \tilde {\gamma }$
, and
$\gamma = \tilde {\gamma }$
, and
 $c(\gamma , \beta ) \leq i$
.
$c(\gamma , \beta ) \leq i$
. -
▸ Otherwise, there is
 $\alpha \in A$
such that
$\alpha \in A$
such that
 $\tilde {\alpha } \geq \gamma $
. But then
$\tilde {\alpha } \geq \gamma $
. But then
 $\tilde {\gamma } = \tilde {\alpha }$
, and hence
$\tilde {\gamma } = \tilde {\alpha }$
, and hence
 $c(\gamma , \beta ) = c(\alpha , \beta ) \leq i$
.
$c(\gamma , \beta ) = c(\alpha , \beta ) \leq i$
.
Claim 4.4.2. c is subadditive.
Proof Suppose that
![]() $\alpha < \beta < \gamma < \kappa $
. To prove subadditivity, there are three cases to consider.
$\alpha < \beta < \gamma < \kappa $
. To prove subadditivity, there are three cases to consider.
-
▸ If
 $\tilde \alpha =\tilde \beta $
, then
$\tilde \alpha =\tilde \beta $
, then
 $c(\alpha ,\beta )=0$
and
$c(\alpha ,\beta )=0$
and
 $c(\alpha ,\gamma )=c(\beta ,\gamma )$
.
$c(\alpha ,\gamma )=c(\beta ,\gamma )$
. -
▸ If
 $\tilde \beta =\tilde \gamma $
, then
$\tilde \beta =\tilde \gamma $
, then
 $c(\alpha ,\beta )=c(\alpha ,\gamma )$
.
$c(\alpha ,\beta )=c(\alpha ,\gamma )$
. -
▸ Otherwise, we have
 $|\{\tilde \alpha ,\tilde \beta ,\tilde \gamma \}|=3$
in which case it is easy to verify that
$|\{\tilde \alpha ,\tilde \beta ,\tilde \gamma \}|=3$
in which case it is easy to verify that
 $c(\alpha ,\beta )\le \max \{c(\alpha ,\gamma ),c(\beta ,\gamma )\}$
and
$c(\alpha ,\beta )\le \max \{c(\alpha ,\gamma ),c(\beta ,\gamma )\}$
and
 $c(\alpha ,\gamma )\le \max \{c(\alpha ,\beta ),c(\beta ,\gamma )\}$
.
$c(\alpha ,\gamma )\le \max \{c(\alpha ,\beta ),c(\beta ,\gamma )\}$
.
To finish the proof, suppose towards a contradiction that c fails to witness
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
. Then there exist
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
. Then there exist
![]() $A\in [\kappa ]^{\kappa }$
and
$A\in [\kappa ]^{\kappa }$
and
![]() $i<\theta $
such that
$i<\theta $
such that
![]() $\sup (c"[A]^2)\le i$
. Set
$\sup (c"[A]^2)\le i$
. Set
![]() $S:=\operatorname {\mathrm {acc}}^+(A)\cap \Gamma $
, note that S is stationary, and let
$S:=\operatorname {\mathrm {acc}}^+(A)\cap \Gamma $
, note that S is stationary, and let
![]() $D:=\bigcup \{ C_{\alpha ,i}\mathrel {|} \alpha \in S\}$
. Then D is a club and
$D:=\bigcup \{ C_{\alpha ,i}\mathrel {|} \alpha \in S\}$
. Then D is a club and
![]() $D \cap \alpha = C_{\alpha , i}$
for all
$D \cap \alpha = C_{\alpha , i}$
for all
![]() $\alpha \in \operatorname {\mathrm {acc}}(D)$
, contradicting the hypothesis that
$\alpha \in \operatorname {\mathrm {acc}}(D)$
, contradicting the hypothesis that
![]() $\vec {C}$
is a
$\vec {C}$
is a
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
-sequence.
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
-sequence.
![]() $(2)\implies (4)$
: Fix a closed, subadditive coloring c witnessing
$(2)\implies (4)$
: Fix a closed, subadditive coloring c witnessing
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2).$
Set
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2).$
Set
![]() $\Gamma :=\operatorname {\mathrm {acc}}(\kappa )\setminus \partial (c)$
, so that
$\Gamma :=\operatorname {\mathrm {acc}}(\kappa )\setminus \partial (c)$
, so that
![]() $\operatorname {\mathrm {acc}}(\kappa ) \cap E^{\kappa }_{\neq \theta } \subseteq \Gamma \subseteq \operatorname {\mathrm {acc}}(\kappa )$
. By Lemma 3.22,
$\operatorname {\mathrm {acc}}(\kappa ) \cap E^{\kappa }_{\neq \theta } \subseteq \Gamma \subseteq \operatorname {\mathrm {acc}}(\kappa )$
. By Lemma 3.22,
Now, let S be a given stationary subset of
![]() $\kappa $
. If
$\kappa $
. If
![]() $S\cap \Gamma $
is stationary, then set
$S\cap \Gamma $
is stationary, then set
![]() $S':=S\cap \Gamma $
; otherwise, set
$S':=S\cap \Gamma $
; otherwise, set
![]() $S':=\kappa $
. Using Lemma 2.4(3), let us fix
$S':=\kappa $
. Using Lemma 2.4(3), let us fix
![]() $\epsilon <\kappa $
such that, for every
$\epsilon <\kappa $
such that, for every
![]() $i<\theta $
,
$i<\theta $
,
![]() $\{\beta \in S'\mathrel {|} \epsilon <\beta , ~ c(\epsilon ,\beta )>i\}$
is stationary.
$\{\beta \in S'\mathrel {|} \epsilon <\beta , ~ c(\epsilon ,\beta )>i\}$
is stationary.
Let
![]() $\alpha \in \Gamma $
be arbitrary. Let
$\alpha \in \Gamma $
be arbitrary. Let
![]() $i'(\alpha )$
be the least
$i'(\alpha )$
be the least
![]() $i < \theta $
for which
$i < \theta $
for which
![]() $\sup (D^c_{\leq i}(\alpha )) = \alpha $
. Next, if
$\sup (D^c_{\leq i}(\alpha )) = \alpha $
. Next, if
![]() $\alpha \le \epsilon $
, then let
$\alpha \le \epsilon $
, then let
![]() $i(\alpha ):=i'(\alpha )$
, and otherwise, let
$i(\alpha ):=i'(\alpha )$
, and otherwise, let
![]() $i(\alpha ):=\max \{i'(\alpha ),c(\epsilon ,\alpha )\}$
. For all
$i(\alpha ):=\max \{i'(\alpha ),c(\epsilon ,\alpha )\}$
. For all
![]() $i \in [i(\alpha ), \theta )$
, let
$i \in [i(\alpha ), \theta )$
, let
![]() $C_{\alpha , i} := D^c_{\leq i}(\alpha )$
. Clearly,
$C_{\alpha , i} := D^c_{\leq i}(\alpha )$
. Clearly,
![]() $\langle C_{\alpha , i} \mathrel {|} i(\alpha ) \leq i < \theta \rangle $
is a
$\langle C_{\alpha , i} \mathrel {|} i(\alpha ) \leq i < \theta \rangle $
is a
![]() $\subseteq $
-increasing sequence of clubs in
$\subseteq $
-increasing sequence of clubs in
![]() $\alpha $
.
$\alpha $
.
We claim that
![]() $\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , ~ i(\alpha ) \leq i < \theta \rangle $
is a
$\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , ~ i(\alpha ) \leq i < \theta \rangle $
is a
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence.
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence.
Claim 4.4.3. Let
![]() $\beta \in \Gamma $
. Then
$\beta \in \Gamma $
. Then
![]() $\Gamma \cap \beta = \bigcup _{i(\beta ) \leq i < \theta } \operatorname {\mathrm {acc}}(C_{\beta , i})$
, and, for all
$\Gamma \cap \beta = \bigcup _{i(\beta ) \leq i < \theta } \operatorname {\mathrm {acc}}(C_{\beta , i})$
, and, for all
![]() $i\in [i(\beta ),\theta )$
and
$i\in [i(\beta ),\theta )$
and
![]() $\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
, we have
$\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
, we have
![]() $i(\alpha ) \leq i$
and
$i(\alpha ) \leq i$
and
![]() $C_{\alpha , i} = C_{\beta , i} \cap \alpha $
.
$C_{\alpha , i} = C_{\beta , i} \cap \alpha $
.
Proof To show the forward inclusion, let
![]() $\alpha \in \Gamma \cap \beta $
be arbitrary. Put
$\alpha \in \Gamma \cap \beta $
be arbitrary. Put
![]() $i:=\max \{i(\alpha ), i(\beta ),c(\alpha , \beta ) \}$
. For all
$i:=\max \{i(\alpha ), i(\beta ),c(\alpha , \beta ) \}$
. For all
![]() $\gamma \in C_{\alpha , i}$
, we have
$\gamma \in C_{\alpha , i}$
, we have
![]() $c(\gamma , \alpha ) \leq i$
and
$c(\gamma , \alpha ) \leq i$
and
![]() $c(\alpha , \beta ) \leq i$
, so, by subadditivity,
$c(\alpha , \beta ) \leq i$
, so, by subadditivity,
![]() $c(\gamma , \beta ) \leq i$
. It follows that
$c(\gamma , \beta ) \leq i$
. It follows that
![]() $\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
.
$\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
.
To show the reverse inclusion and the second statement, let
![]() $i\in [i(\beta ),\theta )$
and
$i\in [i(\beta ),\theta )$
and
![]() $\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
be arbitrary. For all
$\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
be arbitrary. For all
![]() $\gamma \in C_{\beta , i} \cap \alpha $
, we have
$\gamma \in C_{\beta , i} \cap \alpha $
, we have
![]() $c(\gamma , \beta ) \leq i$
and
$c(\gamma , \beta ) \leq i$
and
![]() $c(\alpha , \beta ) \leq i$
, so, by subadditivity,
$c(\alpha , \beta ) \leq i$
, so, by subadditivity,
![]() $c(\gamma , \alpha ) \leq i$
. It follows that
$c(\gamma , \alpha ) \leq i$
. It follows that
![]() $C_{\beta , i} \cap \alpha \subseteq D^c_{\leq i}(\alpha )$
, so
$C_{\beta , i} \cap \alpha \subseteq D^c_{\leq i}(\alpha )$
, so
![]() $\sup (D^c_{\leq i}(\alpha )) = \alpha $
, and hence
$\sup (D^c_{\leq i}(\alpha )) = \alpha $
, and hence
![]() $\alpha \in \Gamma $
,
$\alpha \in \Gamma $
,
![]() $i'(\alpha ) \leq i$
, and
$i'(\alpha ) \leq i$
, and
![]() $C_{\alpha , i} \supseteq C_{\beta , i} \cap \alpha $
. To see that
$C_{\alpha , i} \supseteq C_{\beta , i} \cap \alpha $
. To see that
![]() $i(\alpha )\le i$
, suppose that
$i(\alpha )\le i$
, suppose that
![]() $\alpha>\epsilon $
, and we shall show that
$\alpha>\epsilon $
, and we shall show that
![]() $c(\epsilon ,\alpha )\le i$
. We have already observed that
$c(\epsilon ,\alpha )\le i$
. We have already observed that
![]() $c(\alpha ,\beta )\le i$
. From
$c(\alpha ,\beta )\le i$
. From
![]() $i\ge i(\beta )$
, we infer
$i\ge i(\beta )$
, we infer
![]() $c(\epsilon ,\beta )\le i$
. So, by subadditivity,
$c(\epsilon ,\beta )\le i$
. So, by subadditivity,
![]() $c(\epsilon ,\alpha )\le i$
.
$c(\epsilon ,\alpha )\le i$
.
It remains to show that
![]() $C_{\alpha , i} \subseteq C_{\beta , i} \cap \alpha $
. But, if
$C_{\alpha , i} \subseteq C_{\beta , i} \cap \alpha $
. But, if
![]() $\gamma \in C_{\alpha , i}$
, then
$\gamma \in C_{\alpha , i}$
, then
![]() $c(\gamma , \alpha ) \leq i$
and
$c(\gamma , \alpha ) \leq i$
and
![]() $c(\alpha , \beta ) \leq i$
, so, again by subadditivity, we have
$c(\alpha , \beta ) \leq i$
, so, again by subadditivity, we have
![]() $c(\gamma , \beta ) \leq i$
, and we are done.
$c(\gamma , \beta ) \leq i$
, and we are done.
Claim 4.4.4. Suppose that D is a club in
![]() $\kappa $
. Then there is
$\kappa $
. Then there is
![]() $\alpha \in \operatorname {\mathrm {acc}}(D)\cap \Gamma $
such that, for all
$\alpha \in \operatorname {\mathrm {acc}}(D)\cap \Gamma $
such that, for all
![]() $i \in [i(\alpha ), \theta )$
,
$i \in [i(\alpha ), \theta )$
,
![]() $D\cap \alpha \neq C_{\alpha ,i}$
.
$D\cap \alpha \neq C_{\alpha ,i}$
.
Proof Suppose not. For all
![]() $\alpha \in \operatorname {\mathrm {acc}}(D)$
, fix
$\alpha \in \operatorname {\mathrm {acc}}(D)$
, fix
![]() $j_{\alpha } \in [i(\alpha ), \theta )$
such that
$j_{\alpha } \in [i(\alpha ), \theta )$
such that
![]() $D \cap \alpha = C_{\alpha , j_{\alpha }}$
, and find
$D \cap \alpha = C_{\alpha , j_{\alpha }}$
, and find
![]() $j < \theta $
and
$j < \theta $
and
![]() $A \in [\operatorname {\mathrm {acc}}(D)]^{\kappa }$
such that
$A \in [\operatorname {\mathrm {acc}}(D)]^{\kappa }$
such that
![]() $j_{\alpha } = j$
for all
$j_{\alpha } = j$
for all
![]() $\alpha \in A$
. As c witnesses
$\alpha \in A$
. As c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, we can find
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
, we can find
![]() $(\alpha , \beta ) \in [A]^2$
such that
$(\alpha , \beta ) \in [A]^2$
such that
![]() $c(\alpha , \beta )> j$
. But this contradicts the fact that
$c(\alpha , \beta )> j$
. But this contradicts the fact that
![]() $\alpha \in D \cap \beta = C_{\beta , j}$
, and hence
$\alpha \in D \cap \beta = C_{\beta , j}$
, and hence
![]() $c(\alpha , \beta ) \leq j$
.
$c(\alpha , \beta ) \leq j$
.
Finally, by the choice of
![]() $\epsilon $
, it is clear that if
$\epsilon $
, it is clear that if
![]() $S\cap \Gamma $
is stationary, then for all
$S\cap \Gamma $
is stationary, then for all
![]() $i < \theta $
,
$i < \theta $
,
![]() $\{\alpha \in S\cap \Gamma \mathrel {|} i(\alpha )> i\}$
is stationary.
$\{\alpha \in S\cap \Gamma \mathrel {|} i(\alpha )> i\}$
is stationary.
The proof of the preceding theorem together with Remark 4.3 makes it clear that the following holds as well.
Theorem 4.5. For every
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
, the following are equivalent:
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
, the following are equivalent:
-
(1)
 $\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds.
$\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds. -
(2) There exists a closed witness c to
 $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
for which
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
for which
 $\partial (c)$
is nonstationary.
$\partial (c)$
is nonstationary.
Theorem 4.6. If
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
holds, then so does
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
holds, then so does
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
.
$\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
.
Proof Suppose that
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
holds. By Theorem 4.4, we may fix a closed, subadditive coloring
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
holds. By Theorem 4.4, we may fix a closed, subadditive coloring
![]() $c:[\kappa ]^2\rightarrow \omega $
witnessing
$c:[\kappa ]^2\rightarrow \omega $
witnessing
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
. Let
$\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
. Let
![]() $ \Gamma := \{\alpha \in \operatorname {\mathrm {acc}}(\kappa ) \mathrel {|} \exists i < \omega [\sup (D^c_{\leq i}(\alpha )) = \alpha ]\}, $
so that
$ \Gamma := \{\alpha \in \operatorname {\mathrm {acc}}(\kappa ) \mathrel {|} \exists i < \omega [\sup (D^c_{\leq i}(\alpha )) = \alpha ]\}, $
so that
![]() $\Gamma \supseteq \operatorname {\mathrm {acc}}(\kappa ) \cap E^{\kappa }_{\neq \omega }$
. For all
$\Gamma \supseteq \operatorname {\mathrm {acc}}(\kappa ) \cap E^{\kappa }_{\neq \omega }$
. For all
![]() $\delta \in E^{\kappa }_{\omega }\setminus \Gamma $
, let
$\delta \in E^{\kappa }_{\omega }\setminus \Gamma $
, let
![]() $a_{\delta }:=\{\max (D^c_{\le i}(\delta ))\mathrel {|} i<\omega \ \&\ D^c_{\le i}(\delta )\neq \emptyset \}$
. Clearly,
$a_{\delta }:=\{\max (D^c_{\le i}(\delta ))\mathrel {|} i<\omega \ \&\ D^c_{\le i}(\delta )\neq \emptyset \}$
. Clearly,
![]() $a_{\delta }$
is a cofinal subset of
$a_{\delta }$
is a cofinal subset of
![]() $\delta $
of order-type
$\delta $
of order-type
![]() $\omega $
.
$\omega $
.
For all
![]() $\alpha \in E^{\kappa }_{\omega }\setminus \Gamma $
, let
$\alpha \in E^{\kappa }_{\omega }\setminus \Gamma $
, let
![]() $i(\alpha ):=0$
. For all
$i(\alpha ):=0$
. For all
![]() $\alpha \in \Gamma $
, let
$\alpha \in \Gamma $
, let
![]() $i(\alpha )$
be the least
$i(\alpha )$
be the least
![]() $i < \omega $
for which
$i < \omega $
for which
![]() $\sup (D^c_{\leq i}(\alpha )) = \alpha $
. Then, for all
$\sup (D^c_{\leq i}(\alpha )) = \alpha $
. Then, for all
![]() $\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
and
$\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
and
![]() $i\in [i(\alpha ), \omega )$
, let
$i\in [i(\alpha ), \omega )$
, let
Note that
![]() $C_{\alpha ,i}\subseteq C_{\alpha ,j}$
for all
$C_{\alpha ,i}\subseteq C_{\alpha ,j}$
for all
![]() $j\ge i$
.
$j\ge i$
.
Claim 4.6.1. Let
![]() $\beta \in \operatorname {\mathrm {acc}}(\kappa )$
. Then:
$\beta \in \operatorname {\mathrm {acc}}(\kappa )$
. Then:
-
(1)
 $\operatorname {\mathrm {acc}}(\beta ) = \bigcup _{i(\beta ) \leq i < \omega } \operatorname {\mathrm {acc}}(C_{\beta , i})$
;
$\operatorname {\mathrm {acc}}(\beta ) = \bigcup _{i(\beta ) \leq i < \omega } \operatorname {\mathrm {acc}}(C_{\beta , i})$
; -
(2) for all
 $i\in [i(\beta ),\omega )$
,
$i\in [i(\beta ),\omega )$
,
 $C_{\beta , i}$
is a club in
$C_{\beta , i}$
is a club in
 $\beta $
, and
$\beta $
, and
 $\operatorname {\mathrm {acc}}(C_{\beta ,i})\subseteq D^c_{\le i}(\beta )$
;
$\operatorname {\mathrm {acc}}(C_{\beta ,i})\subseteq D^c_{\le i}(\beta )$
; -
(3) for all
 $i\in [i(\beta ),\omega )$
and
$i\in [i(\beta ),\omega )$
and
 $\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
, we have
$\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
, we have
 $i(\alpha ) \leq i$
and
$i(\alpha ) \leq i$
and
 $C_{\alpha , i} = C_{\beta , i} \cap \alpha $
.
$C_{\alpha , i} = C_{\beta , i} \cap \alpha $
.
Proof (1) Let
![]() $\alpha \in \operatorname {\mathrm {acc}}(\beta )$
be arbitrary. Fix a large enough
$\alpha \in \operatorname {\mathrm {acc}}(\beta )$
be arbitrary. Fix a large enough
![]() $i \geq \max \{i(\alpha ), i(\beta )\}$
such that
$i \geq \max \{i(\alpha ), i(\beta )\}$
such that
![]() $c(\alpha , \beta ) \leq i$
. If
$c(\alpha , \beta ) \leq i$
. If
![]() $\alpha \not \in \Gamma $
, then
$\alpha \not \in \Gamma $
, then
![]() $a_{\alpha }\subseteq C_{\beta ,i}$
. If
$a_{\alpha }\subseteq C_{\beta ,i}$
. If
![]() $\alpha \in \Gamma $
, then for all
$\alpha \in \Gamma $
, then for all
![]() $\gamma \in C_{\alpha , i}$
, we have
$\gamma \in C_{\alpha , i}$
, we have
![]() $c(\gamma , \alpha ) \leq i$
and
$c(\gamma , \alpha ) \leq i$
and
![]() $c(\alpha , \beta ) \leq i$
, so, by subadditivity,
$c(\alpha , \beta ) \leq i$
, so, by subadditivity,
![]() $c(\gamma , \beta ) \leq i$
. Thus, in both cases,
$c(\gamma , \beta ) \leq i$
. Thus, in both cases,
![]() $\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
.
$\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
.
(2) Let
![]() $i\in [i(\beta ),\omega )$
be arbitrary. Suppose first that
$i\in [i(\beta ),\omega )$
be arbitrary. Suppose first that
![]() $\beta \in \Gamma $
. Since
$\beta \in \Gamma $
. Since
![]() $D^c_{\le i}(\beta )$
is a club in
$D^c_{\le i}(\beta )$
is a club in
![]() $\beta $
, to show that
$\beta $
, to show that
![]() $C_{\beta ,i}$
is a club and
$C_{\beta ,i}$
is a club and
![]() $\operatorname {\mathrm {acc}}(C_{\beta , i}) \subseteq D^c_{\leq i}(\beta )$
, it suffices to show that for any pair
$\operatorname {\mathrm {acc}}(C_{\beta , i}) \subseteq D^c_{\leq i}(\beta )$
, it suffices to show that for any pair
![]() $\gamma <\delta $
of successive elements of
$\gamma <\delta $
of successive elements of
![]() $D^c_{\le i}(\beta )$
, if
$D^c_{\le i}(\beta )$
, if
![]() $(\gamma , \delta ) \cap C_{\beta , i} \neq \emptyset $
, then
$(\gamma , \delta ) \cap C_{\beta , i} \neq \emptyset $
, then
![]() $\delta \notin \Gamma $
and
$\delta \notin \Gamma $
and
![]() $(\gamma , \delta ) \cap C_{\beta , i} \subseteq a_{\delta }$
.
$(\gamma , \delta ) \cap C_{\beta , i} \subseteq a_{\delta }$
.
Fix
![]() $\gamma ,\delta $
as above along with
$\gamma ,\delta $
as above along with
![]() $\alpha \in (\gamma ,\delta )\cap C_{\beta ,i}$
. Using the definition of
$\alpha \in (\gamma ,\delta )\cap C_{\beta ,i}$
. Using the definition of
![]() $C_{\beta ,i}$
, let us fix some
$C_{\beta ,i}$
, let us fix some
![]() $\delta '\in D^c_{\leq i}(\beta )\setminus \Gamma $
such that
$\delta '\in D^c_{\leq i}(\beta )\setminus \Gamma $
such that
![]() $\alpha \in a_{\delta '}$
. We have
$\alpha \in a_{\delta '}$
. We have
![]() $c(\delta ',\beta )\le i$
and
$c(\delta ',\beta )\le i$
and
![]() $c(\alpha ,\beta )>i$
. So, by subadditivity,
$c(\alpha ,\beta )>i$
. So, by subadditivity,
![]() $j:=c(\alpha ,\delta ')$
is greater than i. As
$j:=c(\alpha ,\delta ')$
is greater than i. As
![]() $\alpha \in a_{\delta '}$
, it follows that
$\alpha \in a_{\delta '}$
, it follows that
![]() $\alpha =\max (D^c_{\le j}(\delta '))$
.
$\alpha =\max (D^c_{\le j}(\delta '))$
.
Notice that if
![]() $\delta <\delta '$
, then from
$\delta <\delta '$
, then from
![]() $\delta ,\delta '\in D^c_{\le i}$
and subadditivity, we have
$\delta ,\delta '\in D^c_{\le i}$
and subadditivity, we have
![]() $c(\delta ,\delta ')\le i$
, and so
$c(\delta ,\delta ')\le i$
, and so
![]() $\delta \le \max (D^c_{\le i}(\delta '))\le \max (D^c_{\le j}(\delta '))=\alpha $
, which is a contradiction. So
$\delta \le \max (D^c_{\le i}(\delta '))\le \max (D^c_{\le j}(\delta '))=\alpha $
, which is a contradiction. So
![]() $\delta =\delta '$
and
$\delta =\delta '$
and
![]() $\alpha \in a_{\delta }$
, as desired.
$\alpha \in a_{\delta }$
, as desired.
Next, suppose that
![]() $\beta \in \operatorname {\mathrm {acc}}(\kappa )\setminus \Gamma $
. Then the very same argument as before shows that for any pair
$\beta \in \operatorname {\mathrm {acc}}(\kappa )\setminus \Gamma $
. Then the very same argument as before shows that for any pair
![]() $\gamma <\delta $
of successive elements of
$\gamma <\delta $
of successive elements of
![]() $D^c_{\le i}(\beta )$
, if the interval
$D^c_{\le i}(\beta )$
, if the interval
![]() $(\gamma ,\delta )\cap C_{\beta ,i}$
is nonempty, then it is covered by
$(\gamma ,\delta )\cap C_{\beta ,i}$
is nonempty, then it is covered by
![]() $a_{\delta }$
. Moreover, by the definition of
$a_{\delta }$
. Moreover, by the definition of
![]() $C_{\beta , i}$
, we have
$C_{\beta , i}$
, we have
![]() $C_{\beta , i} \setminus \max (D^c_{\leq i}) \subseteq a_{\beta }$
. It follows that
$C_{\beta , i} \setminus \max (D^c_{\leq i}) \subseteq a_{\beta }$
. It follows that
![]() $C_{\beta , i}$
is a club in
$C_{\beta , i}$
is a club in
![]() $\beta $
and
$\beta $
and
![]() $\operatorname {\mathrm {acc}}(C_{\beta , i}) \subseteq D^c_{\leq i}(\beta )$
.
$\operatorname {\mathrm {acc}}(C_{\beta , i}) \subseteq D^c_{\leq i}(\beta )$
.
(3) Fix
![]() $i\in [i(\beta ),\omega )$
and
$i\in [i(\beta ),\omega )$
and
![]() $\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
. In particular,
$\alpha \in \operatorname {\mathrm {acc}}(C_{\beta , i})$
. In particular,
![]() $\alpha \in D^c_{\le i}(\beta )$
, so, by subadditivity,
$\alpha \in D^c_{\le i}(\beta )$
, so, by subadditivity,
![]() $D^c_{\le i}(\alpha )=D^c_{\le i}(\beta )\cap \alpha $
.
$D^c_{\le i}(\alpha )=D^c_{\le i}(\beta )\cap \alpha $
.
-
▸ If
 $\alpha \in \Gamma $
, then
$\alpha \in \Gamma $
, then
 $\alpha \in \operatorname {\mathrm {acc}}(D^c_{\le i}(\beta ))$
, so that
$\alpha \in \operatorname {\mathrm {acc}}(D^c_{\le i}(\beta ))$
, so that
 $i(\alpha )\le i$
, and it is clear from the definition that
$i(\alpha )\le i$
, and it is clear from the definition that
 $C_{\alpha ,i}=C_{\beta ,i}\cap \alpha $
.
$C_{\alpha ,i}=C_{\beta ,i}\cap \alpha $
. -
▸ If
 $\alpha \notin \Gamma $
, then
$\alpha \notin \Gamma $
, then
 $i(\alpha )=0\le i$
, and it is clear from the definition that
$i(\alpha )=0\le i$
, and it is clear from the definition that
 $C_{\alpha ,i}=C_{\beta ,i}\cap \alpha $
.
$C_{\alpha ,i}=C_{\beta ,i}\cap \alpha $
.
The following claim will now finish our proof.
Claim 4.6.2. Suppose that D is a club in
![]() $\kappa $
. Then there is
$\kappa $
. Then there is
![]() $\alpha \in \operatorname {\mathrm {acc}}(D)$
such that, for all
$\alpha \in \operatorname {\mathrm {acc}}(D)$
such that, for all
![]() $i \in [i(\alpha ), \omega )$
,
$i \in [i(\alpha ), \omega )$
,
![]() $D\cap \alpha \neq C_{\alpha ,i}$
.
$D\cap \alpha \neq C_{\alpha ,i}$
.
Proof Suppose not. Then, for all
![]() $\alpha \in \operatorname {\mathrm {acc}}(D)$
, and for some
$\alpha \in \operatorname {\mathrm {acc}}(D)$
, and for some
![]() $j_{\alpha }\in [i(\alpha ),\omega )$
,
$j_{\alpha }\in [i(\alpha ),\omega )$
,
![]() $D\cap \alpha =C_{\alpha ,j_{\alpha }}$
. Find
$D\cap \alpha =C_{\alpha ,j_{\alpha }}$
. Find
![]() $j < \omega $
and
$j < \omega $
and
![]() $A \in [\operatorname {\mathrm {acc}}(D)]^{\kappa }$
such that
$A \in [\operatorname {\mathrm {acc}}(D)]^{\kappa }$
such that
![]() $j_{\alpha } = j$
for all
$j_{\alpha } = j$
for all
![]() $\alpha \in A$
. As c witnesses
$\alpha \in A$
. As c witnesses
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \omega , 2)$
, we may pick
$\operatorname {\mathrm {U}}(\kappa , 2, \omega , 2)$
, we may pick
![]() $(\alpha , \beta )\in [A]^2$
such that
$(\alpha , \beta )\in [A]^2$
such that
![]() $c(\alpha , \beta )> j$
. However
$c(\alpha , \beta )> j$
. However
![]() $\alpha \in \operatorname {\mathrm {acc}}(D\cap \beta )=\operatorname {\mathrm {acc}}(C_{\beta ,j})\subseteq D^c_{\le j}(\beta )$
, meaning that
$\alpha \in \operatorname {\mathrm {acc}}(D\cap \beta )=\operatorname {\mathrm {acc}}(C_{\beta ,j})\subseteq D^c_{\le j}(\beta )$
, meaning that
![]() $c(\alpha ,\beta )\le j$
. This is a contradiction.
$c(\alpha ,\beta )\le j$
. This is a contradiction.
An analogue of the preceding result holds for uncountable
![]() $\theta $
under the additional assumption of stationary reflection.
$\theta $
under the additional assumption of stationary reflection.
Corollary 4.7. Suppose that
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. If every stationary subset of
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. If every stationary subset of
![]() $E^{\kappa }_{\theta }$
reflects, then
$E^{\kappa }_{\theta }$
reflects, then
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
is equivalent to
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
is equivalent to
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
.
$\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
.
Proof Suppose that
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds. By Theorem 4.4, we may then fix a closed, subadditive witness c to
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds. By Theorem 4.4, we may then fix a closed, subadditive witness c to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. As
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. As
![]() $\partial (c)$
is a subset of
$\partial (c)$
is a subset of
![]() $E^{\kappa }_{\theta }$
and every stationary subset of
$E^{\kappa }_{\theta }$
and every stationary subset of
![]() $E^{\kappa }_{\theta }$
reflects, it follows from Lemma 3.31 that
$E^{\kappa }_{\theta }$
reflects, it follows from Lemma 3.31 that
![]() $\partial (c)$
is nonstationary. So, by Theorem 4.5,
$\partial (c)$
is nonstationary. So, by Theorem 4.5,
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds.
$\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds.
We shall now turn to prove Clause (3) of Theorem C, in particular, establishing that, in general, for uncountable
![]() $\theta $
,
$\theta $
,
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
is not equivalent to
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
is not equivalent to
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
. This will follow from the following two theorems; these are fairly straightforward modifications of results of Cummings and Schimmerling [Reference Cummings and Schimmerling9] and Levine and Sinapova [Reference Levine and Sinapova23], respectively, but we provide some details for completeness.
$\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
. This will follow from the following two theorems; these are fairly straightforward modifications of results of Cummings and Schimmerling [Reference Cummings and Schimmerling9] and Levine and Sinapova [Reference Levine and Sinapova23], respectively, but we provide some details for completeness.
Theorem 4.8. Suppose that
![]() $V \subseteq W$
are models of
$V \subseteq W$
are models of
![]() $\textsf{ZFC}$
and
$\textsf{ZFC}$
and
![]() $\theta < \lambda $
are regular cardinals in V such that:
$\theta < \lambda $
are regular cardinals in V such that:
-
(1)
 $\lambda $
is inaccessible in V;
$\lambda $
is inaccessible in V; -
(2)
 $\lambda $
is singular and
$\lambda $
is singular and
 $\operatorname {\mathrm {cf}}(\lambda ) = \theta $
in W;
$\operatorname {\mathrm {cf}}(\lambda ) = \theta $
in W; -
(3)
 $(\lambda ^+)^V = (\lambda ^+)^W$
.
$(\lambda ^+)^V = (\lambda ^+)^W$
.
Then
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\lambda ^+, \theta )$
holds in W. Moreover, in W there is a closed, locally small witness c to
$\boxminus ^{\operatorname {\mathrm {ind}}}(\lambda ^+, \theta )$
holds in W. Moreover, in W there is a closed, locally small witness c to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, 2, \theta , 2)$
such that
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, 2, \theta , 2)$
such that
![]() $\partial (c) \supseteq (E^{\lambda ^+}_{\lambda })^V$
.
$\partial (c) \supseteq (E^{\lambda ^+}_{\lambda })^V$
.
Proof Work first in V, and let
![]() $\Gamma := E^{\lambda ^+}_{<\lambda }$
. Recall that a subset
$\Gamma := E^{\lambda ^+}_{<\lambda }$
. Recall that a subset
![]() $X \subseteq \lambda $
is
$X \subseteq \lambda $
is
![]() $({>}\omega )$
-club if there is a club
$({>}\omega )$
-club if there is a club
![]() $C \subseteq \lambda $
such that
$C \subseteq \lambda $
such that
![]() $C \cap E^{\lambda }_{>\omega } \subseteq X$
. By [Reference Cummings and Schimmerling9, Lemma 4.4], we can fix a matrix
$C \cap E^{\lambda }_{>\omega } \subseteq X$
. By [Reference Cummings and Schimmerling9, Lemma 4.4], we can fix a matrix
![]() $\vec {D} = \langle D_{\alpha , \eta } \mathrel {|} \alpha \in \Gamma , ~ \eta \in X_{\alpha } \rangle $
such that, for all
$\vec {D} = \langle D_{\alpha , \eta } \mathrel {|} \alpha \in \Gamma , ~ \eta \in X_{\alpha } \rangle $
such that, for all
![]() $\alpha \in \Gamma $
,
$\alpha \in \Gamma $
,
-
(1)
 $X_{\alpha }$
is a
$X_{\alpha }$
is a
 $({>}\omega )$
-club subset of
$({>}\omega )$
-club subset of
 $\lambda $
;
$\lambda $
; -
(2) for all
 $\eta \in X_{\alpha }$
,
$\eta \in X_{\alpha }$
,
 $D_{\alpha , \eta }$
is a club in
$D_{\alpha , \eta }$
is a club in
 $\alpha $
and
$\alpha $
and
 $|D_{\alpha , \eta }| < \lambda $
;
$|D_{\alpha , \eta }| < \lambda $
; -
(3)
 $\langle D_{\alpha , \eta } \mathrel {|} \eta \in X_{\alpha } \rangle $
is
$\langle D_{\alpha , \eta } \mathrel {|} \eta \in X_{\alpha } \rangle $
is
 $\subseteq $
-increasing and
$\subseteq $
-increasing and
 $\Gamma \cap \alpha = \bigcup _{\eta \in X_{\alpha }} \operatorname {\mathrm {acc}}(D_{\alpha , \eta })$
;
$\Gamma \cap \alpha = \bigcup _{\eta \in X_{\alpha }} \operatorname {\mathrm {acc}}(D_{\alpha , \eta })$
; -
(4) for all
 $\eta \in X_{\alpha }$
and all
$\eta \in X_{\alpha }$
and all
 $\bar {\alpha } \in \operatorname {\mathrm {acc}}(D_{\alpha , \eta })$
, we have
$\bar {\alpha } \in \operatorname {\mathrm {acc}}(D_{\alpha , \eta })$
, we have
 $\eta \in X_{\bar {\alpha }}$
and
$\eta \in X_{\bar {\alpha }}$
and
 $D_{\bar {\alpha }, \eta } = D_{\alpha , \eta } \cap \bar {\alpha }$
.
$D_{\bar {\alpha }, \eta } = D_{\alpha , \eta } \cap \bar {\alpha }$
.
Now move to W and note that, since
![]() $\operatorname {\mathrm {cf}}(\lambda ) = \theta $
, we have
$\operatorname {\mathrm {cf}}(\lambda ) = \theta $
, we have
![]() $(E^{\lambda ^+}_{\neq \theta } \cap \operatorname {\mathrm {acc}}(\lambda ^+)) \subseteq \Gamma \subseteq \operatorname {\mathrm {acc}}(\lambda ^+)$
. By assumptions (1)–(3) in the statement of the theorem, [Reference Lambie-Hanson18, Corollary 4.2] implies that we can find an increasing sequence of ordinals
$(E^{\lambda ^+}_{\neq \theta } \cap \operatorname {\mathrm {acc}}(\lambda ^+)) \subseteq \Gamma \subseteq \operatorname {\mathrm {acc}}(\lambda ^+)$
. By assumptions (1)–(3) in the statement of the theorem, [Reference Lambie-Hanson18, Corollary 4.2] implies that we can find an increasing sequence of ordinals
![]() $\langle \eta _i \mathrel {|} i < \theta \rangle $
that is cofinal in
$\langle \eta _i \mathrel {|} i < \theta \rangle $
that is cofinal in
![]() $\lambda $
and such that, for all
$\lambda $
and such that, for all
![]() $\alpha \in \Gamma $
, for all sufficiently large
$\alpha \in \Gamma $
, for all sufficiently large
![]() $i < \theta $
, we have
$i < \theta $
, we have
![]() $\delta _i \in X_{\alpha }$
. (This fact is also implicit in the earlier [Reference Džamonja and Shelah11, Theorem 2.0].)
$\delta _i \in X_{\alpha }$
. (This fact is also implicit in the earlier [Reference Džamonja and Shelah11, Theorem 2.0].)
For each
![]() $\alpha \in \Gamma $
, let
$\alpha \in \Gamma $
, let
![]() $i(\alpha )$
be the least
$i(\alpha )$
be the least
![]() $j < \theta $
such that
$j < \theta $
such that
![]() $\delta _i \in X_{\alpha }$
for all
$\delta _i \in X_{\alpha }$
for all
![]() $i \in [j, \theta )$
. Now define a matrix
$i \in [j, \theta )$
. Now define a matrix
![]() $\vec {C} = \langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , i(\alpha ) \leq i < \theta \rangle $
by setting
$\vec {C} = \langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , i(\alpha ) \leq i < \theta \rangle $
by setting
![]() $C_{\alpha , i} := D_{\alpha , \delta _i}$
for all
$C_{\alpha , i} := D_{\alpha , \delta _i}$
for all
![]() $\alpha \in \Gamma $
and all
$\alpha \in \Gamma $
and all
![]() $i \in [i(\alpha ), \theta )$
. Notice that, for all
$i \in [i(\alpha ), \theta )$
. Notice that, for all
![]() $\alpha \in \Gamma $
,
$\alpha \in \Gamma $
,
![]() $i \in [i(\alpha ), \theta )$
, and
$i \in [i(\alpha ), \theta )$
, and
![]() $\bar {\alpha } \in \operatorname {\mathrm {acc}}(C_{\alpha , i})$
, the properties of
$\bar {\alpha } \in \operatorname {\mathrm {acc}}(C_{\alpha , i})$
, the properties of
![]() $\vec {D}$
imply that
$\vec {D}$
imply that
![]() $X_{\alpha } \setminus i \subseteq X_{\bar {\alpha }}$
, and therefore, since
$X_{\alpha } \setminus i \subseteq X_{\bar {\alpha }}$
, and therefore, since
![]() $i \geq i(\alpha )$
we also have
$i \geq i(\alpha )$
we also have
![]() $i \geq i(\bar {\alpha })$
and
$i \geq i(\bar {\alpha })$
and
![]() $C_{\bar {\alpha }, i} = C_{\alpha , i} \cap \bar {\alpha }$
. It is then straightforward to verify that
$C_{\bar {\alpha }, i} = C_{\alpha , i} \cap \bar {\alpha }$
. It is then straightforward to verify that
![]() $\vec {C}$
satisfies Clauses (1)–(3) of Definition 4.2. To verify that
$\vec {C}$
satisfies Clauses (1)–(3) of Definition 4.2. To verify that
![]() $\vec {C}$
satisfies Clause (4) of Definition 4.2, fix a club
$\vec {C}$
satisfies Clause (4) of Definition 4.2, fix a club
![]() $D \subseteq \lambda ^+$
, and let
$D \subseteq \lambda ^+$
, and let
![]() $\alpha \in \operatorname {\mathrm {acc}}(D) \cap \Gamma $
be such that
$\alpha \in \operatorname {\mathrm {acc}}(D) \cap \Gamma $
be such that
![]() $|D \cap \alpha | = \lambda $
. Then, for all
$|D \cap \alpha | = \lambda $
. Then, for all
![]() $i \in [i(\alpha ), \theta )$
, the fact that
$i \in [i(\alpha ), \theta )$
, the fact that
![]() $|C_{\alpha , i}| < \lambda $
implies that
$|C_{\alpha , i}| < \lambda $
implies that
![]() $D \cap \alpha \neq C_{\alpha , i}$
. It follows that
$D \cap \alpha \neq C_{\alpha , i}$
. It follows that
![]() $\vec {C}$
is an
$\vec {C}$
is an
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\lambda ^+, \theta )$
-sequence in W.
$\boxminus ^{\operatorname {\mathrm {ind}}}(\lambda ^+, \theta )$
-sequence in W.
To prove the “moreover” statement, let
![]() $c:[\lambda ^+]^2 \rightarrow \theta $
be the closed witness to
$c:[\lambda ^+]^2 \rightarrow \theta $
be the closed witness to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, 2, \theta , 2)$
derived from
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, 2, \theta , 2)$
derived from
![]() $\vec {C}$
as in the proof of
$\vec {C}$
as in the proof of
![]() $(1)\implies (2)$
of Theorem 4.4. The fact that
$(1)\implies (2)$
of Theorem 4.4. The fact that
![]() $\partial (c) \supseteq (E^{\lambda ^+}_{\lambda })^V$
follows immediately from our definition of
$\partial (c) \supseteq (E^{\lambda ^+}_{\lambda })^V$
follows immediately from our definition of
![]() $\Gamma $
, and the fact that c is locally small follows immediately from the fact that
$\Gamma $
, and the fact that c is locally small follows immediately from the fact that
![]() $|C_{\alpha , i}| < \lambda $
for all
$|C_{\alpha , i}| < \lambda $
for all
![]() $\alpha \in \Gamma $
and
$\alpha \in \Gamma $
and
![]() $i \in [i(\alpha ), \theta )$
.
$i \in [i(\alpha ), \theta )$
.
Theorem 4.9. Suppose that
![]() $\theta <\lambda <\kappa $
are regular uncountable cardinals such that
$\theta <\lambda <\kappa $
are regular uncountable cardinals such that
![]() $\lambda $
is supercompact and
$\lambda $
is supercompact and
![]() $\kappa $
is weakly compact. Then there is a forcing extension in which
$\kappa $
is weakly compact. Then there is a forcing extension in which
![]() $\lambda $
is a singular strong limit of cofinality
$\lambda $
is a singular strong limit of cofinality
![]() $\theta $
,
$\theta $
,
![]() $\kappa =\lambda ^+$
,
$\kappa =\lambda ^+$
,
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds, and
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\theta )$
holds, and
![]() $\square (\kappa ,\tau )$
fails for all
$\square (\kappa ,\tau )$
fails for all
![]() $\tau <\lambda $
.
$\tau <\lambda $
.
Proof By forcing with the Laver preparation forcing if necessary, we may assume that the supercompactness of
![]() $\lambda $
is indestructible under
$\lambda $
is indestructible under
![]() $\lambda $
-directed closed forcing. Following [Reference Levine and Sinapova23, Section 4], let
$\lambda $
-directed closed forcing. Following [Reference Levine and Sinapova23, Section 4], let
![]() $\mathbb {C} := \mathrm {Coll}(\lambda , {<}\kappa )$
, and let
$\mathbb {C} := \mathrm {Coll}(\lambda , {<}\kappa )$
, and let
![]() $\dot {\mathbb {M}}$
be a
$\dot {\mathbb {M}}$
be a
![]() $\mathbb {C}$
-name for the Magidor forcing that turns
$\mathbb {C}$
-name for the Magidor forcing that turns
![]() $\lambda $
into a singular cardinal of cofinality
$\lambda $
into a singular cardinal of cofinality
![]() $\theta $
.
$\theta $
.
For every inaccessible
![]() $\delta < \kappa $
above
$\delta < \kappa $
above
![]() $\lambda $
, let
$\lambda $
, let
![]() $\mathbb {C}_{\delta } := \mathrm {Coll}(\lambda , {<}\delta )$
. By [Reference Levine and Sinapova23, Proposition 4.3], there is a club
$\mathbb {C}_{\delta } := \mathrm {Coll}(\lambda , {<}\delta )$
. By [Reference Levine and Sinapova23, Proposition 4.3], there is a club
![]() $C \subseteq \kappa $
such that, for every inaccessible
$C \subseteq \kappa $
such that, for every inaccessible
![]() $\delta \in C$
,
$\delta \in C$
,
![]() $\dot {\mathbb {M}}_{\delta } := \dot {\mathbb {M}} \cap V_{\delta }$
is a
$\dot {\mathbb {M}}_{\delta } := \dot {\mathbb {M}} \cap V_{\delta }$
is a
![]() $\mathbb {C}_{\delta }$
-name for a Magidor forcing to turn
$\mathbb {C}_{\delta }$
-name for a Magidor forcing to turn
![]() $\lambda $
into a singular cardinal of cofinality
$\lambda $
into a singular cardinal of cofinality
![]() $\theta $
such that there is a complete embedding of
$\theta $
such that there is a complete embedding of
![]() $\mathbb {C}_{\delta } \ast \dot {\mathbb {M}}_{\delta }$
into
$\mathbb {C}_{\delta } \ast \dot {\mathbb {M}}_{\delta }$
into
![]() $\mathbb {C} \ast \dot {\mathbb {M}}$
.
$\mathbb {C} \ast \dot {\mathbb {M}}$
.
In
![]() $V^{\mathbb {C}}$
,
$V^{\mathbb {C}}$
,
![]() $\mathbb {M}$
has the
$\mathbb {M}$
has the
![]() $\lambda ^+$
-cc and thus preserves
$\lambda ^+$
-cc and thus preserves
![]() $\lambda ^+$
. Therefore, applying Theorem 4.8 to the models
$\lambda ^+$
. Therefore, applying Theorem 4.8 to the models
![]() $V^{\mathbb {C}}$
and
$V^{\mathbb {C}}$
and
![]() $V^{\mathbb {C} * \dot {\mathbb {M}}}$
shows that
$V^{\mathbb {C} * \dot {\mathbb {M}}}$
shows that
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
holds in
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
holds in
![]() $V^{\mathbb {C} * \dot {\mathbb {M}}}$
. It remains to show that
$V^{\mathbb {C} * \dot {\mathbb {M}}}$
. It remains to show that
![]() $\square (\kappa , \tau )$
fails for every
$\square (\kappa , \tau )$
fails for every
![]() $\tau < \lambda $
.
$\tau < \lambda $
.
Suppose for the sake of contradiction that
![]() $\tau < \lambda $
and
$\tau < \lambda $
and
![]() $\dot {\mathcal {D}} = \langle \dot {\mathcal {D}}_{\alpha } \mathrel {|} \alpha \in \operatorname {\mathrm {acc}}(\kappa ) \rangle $
is a
$\dot {\mathcal {D}} = \langle \dot {\mathcal {D}}_{\alpha } \mathrel {|} \alpha \in \operatorname {\mathrm {acc}}(\kappa ) \rangle $
is a
![]() $\mathbb {C} * \dot {\mathbb {M}}$
-name for a
$\mathbb {C} * \dot {\mathbb {M}}$
-name for a
![]() $\square (\kappa , \tau )$
-sequence. This is a
$\square (\kappa , \tau )$
-sequence. This is a
![]() $\Pi ^1_1$
statement about the structure
$\Pi ^1_1$
statement about the structure
![]() $(V_{\kappa }, \in , \mathbb {C} * \dot {\mathbb {M}}, \dot {\mathcal {D}})$
(the sole universal quantification over subsets of
$(V_{\kappa }, \in , \mathbb {C} * \dot {\mathbb {M}}, \dot {\mathcal {D}})$
(the sole universal quantification over subsets of
![]() $V_{\kappa }$
is the assertion that there exists no
$V_{\kappa }$
is the assertion that there exists no
![]() $\mathbb {C} * \dot {\mathbb {M}}$
-name for a thread through
$\mathbb {C} * \dot {\mathbb {M}}$
-name for a thread through
![]() $\dot {\mathcal {D}}$
). Therefore, by the weak compactness of
$\dot {\mathcal {D}}$
). Therefore, by the weak compactness of
![]() $\kappa $
, we can find an inaccessible
$\kappa $
, we can find an inaccessible
![]() $\delta \in C$
such that
$\delta \in C$
such that
![]() $\dot {\mathcal {D}}^* := \dot {\mathcal {D}} \cap V_{\delta }$
is a
$\dot {\mathcal {D}}^* := \dot {\mathcal {D}} \cap V_{\delta }$
is a
![]() $\mathbb {C}_{\delta } * \dot {\mathbb {M}}_{\delta }$
-name for a
$\mathbb {C}_{\delta } * \dot {\mathbb {M}}_{\delta }$
-name for a
![]() $\square (\delta , \tau )$
-sequence.
$\square (\delta , \tau )$
-sequence.
Note that
![]() $\delta = \lambda ^+$
in
$\delta = \lambda ^+$
in
![]() $V^{\mathbb {C}_{\delta } * \dot {\mathbb {M}}_{\delta }}$
. In
$V^{\mathbb {C}_{\delta } * \dot {\mathbb {M}}_{\delta }}$
. In
![]() $V^{\mathbb {C} * \dot {\mathbb {M}}}$
, we have
$V^{\mathbb {C} * \dot {\mathbb {M}}}$
, we have
![]() $\operatorname {\mathrm {cf}}(\delta ) = \theta> \omega $
. Therefore, in
$\operatorname {\mathrm {cf}}(\delta ) = \theta> \omega $
. Therefore, in
![]() $V^{\mathbb {C} * \dot {\mathbb {M}}}$
, any element of
$V^{\mathbb {C} * \dot {\mathbb {M}}}$
, any element of
![]() $\mathcal {D}_{\delta }$
is a thread through
$\mathcal {D}_{\delta }$
is a thread through
![]() $\mathcal {D}^*$
. However, the proof of [Reference Levine and Sinapova23, Lemma 4.7] shows that forcing over
$\mathcal {D}^*$
. However, the proof of [Reference Levine and Sinapova23, Lemma 4.7] shows that forcing over
![]() $V^{\mathbb {C}_{\delta } * \dot {\mathbb {M}}_{\delta }}$
with
$V^{\mathbb {C}_{\delta } * \dot {\mathbb {M}}_{\delta }}$
with
![]() $(\mathbb {C} * \dot {\mathbb {M}})/(\mathbb {C}_{\delta } * \dot {\mathbb {M}}_{\delta })$
cannot add a thread to a
$(\mathbb {C} * \dot {\mathbb {M}})/(\mathbb {C}_{\delta } * \dot {\mathbb {M}}_{\delta })$
cannot add a thread to a
![]() $\square (\delta , \tau )$
-sequence. ([Reference Levine and Sinapova23, Lemma 4.7] is about
$\square (\delta , \tau )$
-sequence. ([Reference Levine and Sinapova23, Lemma 4.7] is about
![]() $\square _{\lambda , \tau }$
-sequences, but the exact same proof still works for
$\square _{\lambda , \tau }$
-sequences, but the exact same proof still works for
![]() $\square (\delta , \tau )$
-sequences.) This is a contradiction, thus completing the proof.
$\square (\delta , \tau )$
-sequences.) This is a contradiction, thus completing the proof.
Remark 4.10. Suppose that
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
is such that there exists a closed subadditive witness to
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
is such that there exists a closed subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. By Lemma 3.10, if
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
. By Lemma 3.10, if
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\theta $
-inaccessible, then there exists a
${<}\theta $
-inaccessible, then there exists a
![]() $\kappa $
-Aronszajn tree with a
$\kappa $
-Aronszajn tree with a
![]() $\theta $
-ascent path. In particular, such a tree exists in the model of Theorem 4.9. We note that by a combination of Theorem 4.4, [Reference Brodsky and Rinot4, Theorem 6.11] and a minor variation of [Reference Brodsky and Rinot4, Theorem 4.44], if
$\theta $
-ascent path. In particular, such a tree exists in the model of Theorem 4.9. We note that by a combination of Theorem 4.4, [Reference Brodsky and Rinot4, Theorem 6.11] and a minor variation of [Reference Brodsky and Rinot4, Theorem 4.44], if
![]() $\kappa =\kappa ^{<\kappa }$
is a successor cardinal which is
$\kappa =\kappa ^{<\kappa }$
is a successor cardinal which is
![]() $\theta $
-inaccessible, then there moreover exists a
$\theta $
-inaccessible, then there moreover exists a
![]() $\kappa $
-Souslin tree with a
$\kappa $
-Souslin tree with a
![]() $\theta $
-ascent path.
$\theta $
-ascent path.
The Mapping Reflection Principle (
![]() $\textsf {MRP}$
), introduced by Moore in [Reference Magidor and Shelah26], is a useful consequence of
$\textsf {MRP}$
), introduced by Moore in [Reference Magidor and Shelah26], is a useful consequence of
![]() $\textsf {PFA}$
.
$\textsf {PFA}$
.
Corollary 4.11.
![]() $\textsf {MRP}$
implies that for every regular cardinal
$\textsf {MRP}$
implies that for every regular cardinal
![]() $\kappa \ge \aleph _2$
, there exists no closed, subadditive witness to
$\kappa \ge \aleph _2$
, there exists no closed, subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
.
$\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
.
Proof By Theorems 4.4 and 4.6, if there exists a closed subadditive witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
, then
$\operatorname {\mathrm {U}}(\kappa ,2,\omega ,2)$
, then
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
holds. In particular,
$\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
holds. In particular,
![]() $\square (\kappa ,\omega )$
holds. However, by [Reference Strullu32, Theorem 1.8], for every regular cardinal
$\square (\kappa ,\omega )$
holds. However, by [Reference Strullu32, Theorem 1.8], for every regular cardinal
![]() $\kappa \ge \aleph _2$
,
$\kappa \ge \aleph _2$
,
![]() $\square (\kappa ,\omega )$
is refuted by
$\square (\kappa ,\omega )$
is refuted by
![]() $\textsf {MRP}$
. This is also implicit in [Reference Viale35, Section 7].
$\textsf {MRP}$
. This is also implicit in [Reference Viale35, Section 7].
Remark 4.12. In [Reference Strullu32], Strullu proves that
![]() $\textsf {MRP} + \textsf {MA}_{\omega _1}$
refutes
$\textsf {MRP} + \textsf {MA}_{\omega _1}$
refutes
![]() $\square (\kappa , \omega _1)$
for all regular
$\square (\kappa , \omega _1)$
for all regular
![]() $\kappa \geq \aleph _2$
. In light of this fact and Theorem 3.45, it is natural to ask whether
$\kappa \geq \aleph _2$
. In light of this fact and Theorem 3.45, it is natural to ask whether
![]() $\textsf {MRP}+\textsf {MA}_{\omega _1}$
moreover refutes
$\textsf {MRP}+\textsf {MA}_{\omega _1}$
moreover refutes
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega _1)$
. In an upcoming paper, it will be shown that
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega _1)$
. In an upcoming paper, it will be shown that
![]() $\textsf {MM}$
is compatible with
$\textsf {MM}$
is compatible with
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega _1)$
for any choice of a regular cardinal
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega _1)$
for any choice of a regular cardinal
![]() $\kappa \ge \aleph _2$
. It follows that
$\kappa \ge \aleph _2$
. It follows that
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\omega _2,\omega _1)$
does not imply the existence of an
$\boxminus ^{\operatorname {\mathrm {ind}}}(\omega _2,\omega _1)$
does not imply the existence of an
![]() $\omega _2$
-Aronszajn tree. Thus, the arithmetic hypothesis in Lemma 3.10 cannot be waived.
$\omega _2$
-Aronszajn tree. Thus, the arithmetic hypothesis in Lemma 3.10 cannot be waived.
By [Reference Lambie-Hanson and Lücke19, Theorem 3.4], for every
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
,
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
,
![]() $\square (\kappa )$
implies
$\square (\kappa )$
implies
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
. Essentially the same proof of that theorem establishes that for every
$\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
. Essentially the same proof of that theorem establishes that for every
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
,
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
,
![]() $\square (\kappa , \sqsubseteq _{\theta })$
implies
$\square (\kappa , \sqsubseteq _{\theta })$
implies
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
. Here, we shall prove a generalization that also yields the second part of Theorem A.
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
. Here, we shall prove a generalization that also yields the second part of Theorem A.
Theorem 4.13. Suppose that
![]() $\kappa \ge \aleph _2$
,
$\kappa \ge \aleph _2$
,
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
,
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
,
![]() $T \subseteq E^{\kappa }_{\theta }$
, and there is a
$T \subseteq E^{\kappa }_{\theta }$
, and there is a
![]() $\square (\kappa , \sqsubseteq _{\theta })$
-sequence that avoids T. Then:
$\square (\kappa , \sqsubseteq _{\theta })$
-sequence that avoids T. Then:
-
(1) There is a
 $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence
 $\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , ~ i(\alpha ) \leq i < \theta \rangle $
such that
$\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , ~ i(\alpha ) \leq i < \theta \rangle $
such that
 $\Gamma \cap T = \emptyset $
.
$\Gamma \cap T = \emptyset $
. -
(2) There is a closed witness c to
 $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
such that
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,2,\theta ,2)$
such that
 $T \subseteq \partial (c)$
.
$T \subseteq \partial (c)$
.
Proof The proof of Theorem 4.4 makes it clear that
![]() $(1)\implies (2)$
, so we focus on proving Clause (1). Fix a
$(1)\implies (2)$
, so we focus on proving Clause (1). Fix a
![]() $\square (\kappa , \sqsubseteq _{\theta })$
-sequence
$\square (\kappa , \sqsubseteq _{\theta })$
-sequence
![]() $\vec C=\langle C_{\beta } \mathrel {|} \beta < \kappa \rangle $
that avoids T, i.e., for all
$\vec C=\langle C_{\beta } \mathrel {|} \beta < \kappa \rangle $
that avoids T, i.e., for all
![]() $\beta < \kappa $
, we have
$\beta < \kappa $
, we have
![]() $\operatorname {\mathrm {acc}}(C_{\beta }) \cap T = \emptyset $
. Set
$\operatorname {\mathrm {acc}}(C_{\beta }) \cap T = \emptyset $
. Set
![]() $\Delta :=\{\delta \in \operatorname {\mathrm {acc}}(\kappa )\mathrel {|} \forall \bar \delta \in \operatorname {\mathrm {acc}}(C_{\delta })[C_{\bar \delta }=C_{\delta }\cap \bar \delta ]\}$
. By the
$\Delta :=\{\delta \in \operatorname {\mathrm {acc}}(\kappa )\mathrel {|} \forall \bar \delta \in \operatorname {\mathrm {acc}}(C_{\delta })[C_{\bar \delta }=C_{\delta }\cap \bar \delta ]\}$
. By the
![]() $\sqsubseteq _{\theta }$
-coherence of
$\sqsubseteq _{\theta }$
-coherence of
![]() $\vec {C}$
, we have
$\vec {C}$
, we have
![]() $E^{\kappa }_{\geq \theta } \subseteq \Delta $
. Set
$E^{\kappa }_{\geq \theta } \subseteq \Delta $
. Set
![]() $\Omega := E^{\kappa }_{>\theta } \cup \bigcup \{ \operatorname {\mathrm {acc}}(C_{\delta })\mathrel {|} \delta \in \Delta \}$
, and note that
$\Omega := E^{\kappa }_{>\theta } \cup \bigcup \{ \operatorname {\mathrm {acc}}(C_{\delta })\mathrel {|} \delta \in \Delta \}$
, and note that
![]() $\Omega \subseteq \Delta \setminus T$
. As
$\Omega \subseteq \Delta \setminus T$
. As
![]() $\kappa \ge \aleph _2$
,
$\kappa \ge \aleph _2$
,
![]() $\Omega $
is stationary. So, by [Reference Brodsky and Rinot3, Lemmas 1.23 and 1.7], we may fix
$\Omega $
is stationary. So, by [Reference Brodsky and Rinot3, Lemmas 1.23 and 1.7], we may fix
![]() $\zeta <\kappa $
such that
$\zeta <\kappa $
such that
![]() $\{\beta \in \Omega \mathrel {|} \operatorname {\mathrm {otp}}(C_{\beta })> \zeta \text { and } C_{\beta }(\zeta ) \geq \tau \}$
is stationary for all
$\{\beta \in \Omega \mathrel {|} \operatorname {\mathrm {otp}}(C_{\beta })> \zeta \text { and } C_{\beta }(\zeta ) \geq \tau \}$
is stationary for all
![]() $\tau < \kappa $
. By successive applications of Fodor’s Lemma, we may then recursively construct a strictly increasing sequence of ordinals
$\tau < \kappa $
. By successive applications of Fodor’s Lemma, we may then recursively construct a strictly increasing sequence of ordinals
![]() $\langle \tau _i\mathrel {|} i<\theta \rangle $
such that
$\langle \tau _i\mathrel {|} i<\theta \rangle $
such that
![]() $\tau _0>\min (\Omega )$
and such that, for every
$\tau _0>\min (\Omega )$
and such that, for every
![]() $i<\theta $
,
$i<\theta $
,
![]() $\{\beta \in \Omega \mathrel {|} \operatorname {\mathrm {otp}}(C_{\beta })> \zeta \text { and } C_{\beta }(\zeta ) = \tau _i\}$
is stationary.
$\{\beta \in \Omega \mathrel {|} \operatorname {\mathrm {otp}}(C_{\beta })> \zeta \text { and } C_{\beta }(\zeta ) = \tau _i\}$
is stationary.
Next, define
![]() $\vec {D} = \langle D_{\beta } \mathrel {|} \beta < \kappa \rangle $
, as follows:
$\vec {D} = \langle D_{\beta } \mathrel {|} \beta < \kappa \rangle $
, as follows:
-
• Let
 $D_0:=\emptyset $
.
$D_0:=\emptyset $
. -
• For every
 $\beta <\kappa $
, let
$\beta <\kappa $
, let
 $D_{\beta +1}:=\{\beta \}$
.
$D_{\beta +1}:=\{\beta \}$
. -
• For every
 $\beta \in \Delta $
such that
$\beta \in \Delta $
such that
 $\operatorname {\mathrm {otp}}(C_{\beta })\le \zeta $
, let
$\operatorname {\mathrm {otp}}(C_{\beta })\le \zeta $
, let
 $D_{\beta }:=C_{\beta }$
.
$D_{\beta }:=C_{\beta }$
. -
• For every
 $\beta \in \Delta $
such that
$\beta \in \Delta $
such that
 $\operatorname {\mathrm {otp}}(C_{\beta })>\zeta $
, let
$\operatorname {\mathrm {otp}}(C_{\beta })>\zeta $
, let
 $D_{\beta }:=C_{\beta }\setminus C_{\beta }(\zeta )$
.
$D_{\beta }:=C_{\beta }\setminus C_{\beta }(\zeta )$
. -
• For every
 $\beta \in \operatorname {\mathrm {acc}}(\kappa )\setminus \Delta $
, pick a club
$\beta \in \operatorname {\mathrm {acc}}(\kappa )\setminus \Delta $
, pick a club
 $D_{\beta }$
in
$D_{\beta }$
in
 $\beta $
of order-type
$\beta $
of order-type
 $\operatorname {\mathrm {cf}}(\beta )$
such that
$\operatorname {\mathrm {cf}}(\beta )$
such that
 $D_{\beta }\cap T=\emptyset $
.
$D_{\beta }\cap T=\emptyset $
.
For every ordinal
![]() $\beta <\kappa $
, let
$\beta <\kappa $
, let
 $$ \begin{align*}j(\beta):=\begin{cases} i,&\text{if }\min(D_{\beta})=\delta_i,\\ 0,&\text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}j(\beta):=\begin{cases} i,&\text{if }\min(D_{\beta})=\delta_i,\\ 0,&\text{otherwise}. \end{cases}\end{align*} $$
For every
![]() $i<\theta $
, set
$i<\theta $
, set
![]() $\Gamma _i:=\{\beta \in \Omega \mathrel {|} j(\beta )=i\}$
. Then set
$\Gamma _i:=\{\beta \in \Omega \mathrel {|} j(\beta )=i\}$
. Then set
![]() $\Gamma := \Omega \cup (\operatorname {\mathrm {acc}}(\kappa )\cap E^{\kappa }_{<\theta })$
.
$\Gamma := \Omega \cup (\operatorname {\mathrm {acc}}(\kappa )\cap E^{\kappa }_{<\theta })$
.
Claim 4.13.1.
-
(1)
 $(E^{\kappa }_{\neq \theta } \cap \operatorname {\mathrm {acc}}(\kappa )) \subseteq \Gamma \subseteq \operatorname {\mathrm {acc}}(\kappa )$
and
$(E^{\kappa }_{\neq \theta } \cap \operatorname {\mathrm {acc}}(\kappa )) \subseteq \Gamma \subseteq \operatorname {\mathrm {acc}}(\kappa )$
and
 $\Gamma \cap T=\emptyset $
.
$\Gamma \cap T=\emptyset $
. -
(2) For all
 $\beta \in \Delta $
and
$\beta \in \Delta $
and
 $\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })$
, we have:
$\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })$
, we have:-
•
 $\alpha \in \Omega $
,
$\alpha \in \Omega $
, -
•
 $D_{\alpha } = D_{\beta } \cap \alpha $
, and
$D_{\alpha } = D_{\beta } \cap \alpha $
, and -
•
 $j(\alpha )=j(\beta )$
.
$j(\alpha )=j(\beta )$
.
-
-
(3) For every
 $\beta \in \Gamma \setminus \operatorname {\mathrm {acc}}^+(\Gamma )$
, we have
$\beta \in \Gamma \setminus \operatorname {\mathrm {acc}}^+(\Gamma )$
, we have
 $\operatorname {\mathrm {otp}}(D_{\beta }\setminus \sup (\Gamma \cap \beta ))=\omega $
.
$\operatorname {\mathrm {otp}}(D_{\beta }\setminus \sup (\Gamma \cap \beta ))=\omega $
. -
(4) For every
 $i<\theta $
,
$i<\theta $
,
 $\Gamma _i$
is stationary.
$\Gamma _i$
is stationary. -
(5)
 $\min (\Omega )\in \Gamma _0$
.
$\min (\Omega )\in \Gamma _0$
.
Proof
-
(1) This follows directly from the definition of
 $\Gamma $
.
$\Gamma $
. -
(2) Let
 $\beta \in \Delta $
and
$\beta \in \Delta $
and
 $\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })$
be arbitrary. There two cases to consider:
$\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })$
be arbitrary. There two cases to consider:-
▸ If
 $\operatorname {\mathrm {otp}}(C_{\beta })\le \zeta $
, then
$\operatorname {\mathrm {otp}}(C_{\beta })\le \zeta $
, then
 $\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })=\operatorname {\mathrm {acc}}(C_{\beta })$
, so
$\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })=\operatorname {\mathrm {acc}}(C_{\beta })$
, so
 $C_{\alpha }=C_{\beta }\cap \alpha $
and
$C_{\alpha }=C_{\beta }\cap \alpha $
and
 $\operatorname {\mathrm {otp}}(C_{\alpha })<\zeta $
. Since
$\operatorname {\mathrm {otp}}(C_{\alpha })<\zeta $
. Since
 $\beta \in \Delta $
and
$\beta \in \Delta $
and
 $\alpha \in \operatorname {\mathrm {acc}}(C_{\beta })$
, the definition of
$\alpha \in \operatorname {\mathrm {acc}}(C_{\beta })$
, the definition of
 $\Omega $
implies that
$\Omega $
implies that
 $\alpha \in \Omega \subseteq \Delta $
. We therefore have
$\alpha \in \Omega \subseteq \Delta $
. We therefore have
 $D_{\alpha } = C_{\alpha } = C_{\beta } \cap \alpha = D_{\beta } \cap \alpha $
. In particular,
$D_{\alpha } = C_{\alpha } = C_{\beta } \cap \alpha = D_{\beta } \cap \alpha $
. In particular,
 $\min (D_{\alpha }) = \min (D_{\beta })$
, so
$\min (D_{\alpha }) = \min (D_{\beta })$
, so
 $j(\alpha )=j(\beta )$
.
$j(\alpha )=j(\beta )$
. -
▸ If
 $\operatorname {\mathrm {otp}}(C_{\beta })>\zeta $
, then
$\operatorname {\mathrm {otp}}(C_{\beta })>\zeta $
, then
 $\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })=\operatorname {\mathrm {acc}}(C_{\beta }\setminus C_{\beta }(\zeta ))$
, so
$\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })=\operatorname {\mathrm {acc}}(C_{\beta }\setminus C_{\beta }(\zeta ))$
, so
 $C_{\alpha }=C_{\beta }\cap \alpha $
and
$C_{\alpha }=C_{\beta }\cap \alpha $
and
 $\operatorname {\mathrm {otp}}(C_{\alpha })>\zeta $
. As in the previous case, we have
$\operatorname {\mathrm {otp}}(C_{\alpha })>\zeta $
. As in the previous case, we have
 $\alpha \in \Omega \subseteq \Delta $
, and therefore
$\alpha \in \Omega \subseteq \Delta $
, and therefore
 $D_{\alpha } = C_{\alpha }\setminus C_{\alpha }(\zeta )=(C_{\beta }\setminus C_{\beta }(\zeta ))\cap \alpha =D_{\beta }\cap \alpha $
. In particular,
$D_{\alpha } = C_{\alpha }\setminus C_{\alpha }(\zeta )=(C_{\beta }\setminus C_{\beta }(\zeta ))\cap \alpha =D_{\beta }\cap \alpha $
. In particular,
 $j(\alpha )=j(\beta )$
.
$j(\alpha )=j(\beta )$
.
-
-
(3) Let
 $\beta \in \Gamma $
. Note the following:
$\beta \in \Gamma $
. Note the following:-
▸ If
 $\omega < \operatorname {\mathrm {cf}}(\beta )\le \theta $
, then
$\omega < \operatorname {\mathrm {cf}}(\beta )\le \theta $
, then
 $E^{\beta }_{\omega }\subseteq \operatorname {\mathrm {acc}}(\kappa )\cap E^{\kappa }_{<\theta }\subseteq \Gamma $
, and hence
$E^{\beta }_{\omega }\subseteq \operatorname {\mathrm {acc}}(\kappa )\cap E^{\kappa }_{<\theta }\subseteq \Gamma $
, and hence
 $\beta \in \operatorname {\mathrm {acc}}^+(\Gamma )$
.
$\beta \in \operatorname {\mathrm {acc}}^+(\Gamma )$
. -
▸ If
 $\operatorname {\mathrm {cf}}(\beta )>\theta $
, then
$\operatorname {\mathrm {cf}}(\beta )>\theta $
, then
 $\operatorname {\mathrm {acc}}(C_{\beta })\subseteq \Omega \subseteq \Gamma $
, so again
$\operatorname {\mathrm {acc}}(C_{\beta })\subseteq \Omega \subseteq \Gamma $
, so again
 $\beta \in \operatorname {\mathrm {acc}}^+(\Gamma )$
.
$\beta \in \operatorname {\mathrm {acc}}^+(\Gamma )$
.
Therefore, if
 $\beta \in \Gamma \setminus \operatorname {\mathrm {acc}}^+(\Gamma )$
, then
$\beta \in \Gamma \setminus \operatorname {\mathrm {acc}}^+(\Gamma )$
, then
 $\operatorname {\mathrm {cf}}(\beta )=\omega $
. So, if
$\operatorname {\mathrm {cf}}(\beta )=\omega $
. So, if
 $\operatorname {\mathrm {otp}}(D_{\beta })>\omega $
, then
$\operatorname {\mathrm {otp}}(D_{\beta })>\omega $
, then
 $\beta \in \Delta $
, and then
$\beta \in \Delta $
, and then
 $\operatorname {\mathrm {acc}}(C_{\beta })\subseteq \Omega \subseteq \Gamma $
. As we assume that
$\operatorname {\mathrm {acc}}(C_{\beta })\subseteq \Omega \subseteq \Gamma $
. As we assume that
 $\beta \notin \operatorname {\mathrm {acc}}^+(\Gamma )$
, it in particular follows that
$\beta \notin \operatorname {\mathrm {acc}}^+(\Gamma )$
, it in particular follows that
 $\sup (\operatorname {\mathrm {acc}}(C_{\beta }))<\beta $
, and
$\sup (\operatorname {\mathrm {acc}}(C_{\beta }))<\beta $
, and
 $\operatorname {\mathrm {otp}}(C_{\beta }\setminus \sup (\Gamma \cap \beta ))=\omega $
. As
$\operatorname {\mathrm {otp}}(C_{\beta }\setminus \sup (\Gamma \cap \beta ))=\omega $
. As
 $D_{\beta }$
is a final segment of
$D_{\beta }$
is a final segment of
 $C_{\beta }$
, it also follows that
$C_{\beta }$
, it also follows that
 $\operatorname {\mathrm {otp}}(D_{\beta }\setminus \sup (\Gamma \cap \beta ))=\omega $
.
$\operatorname {\mathrm {otp}}(D_{\beta }\setminus \sup (\Gamma \cap \beta ))=\omega $
. -
-
(4) This follows directly from the choice of
 $\langle \tau _i\mathrel {|} i<\theta \rangle $
.
$\langle \tau _i\mathrel {|} i<\theta \rangle $
. -
(5) For every
 $i<\theta $
, we have
$i<\theta $
, we have
 $\tau _i\ge \tau _0>\min (\Omega )$
, so it is impossible for
$\tau _i\ge \tau _0>\min (\Omega )$
, so it is impossible for
 $j(\min (\Omega ))$
to be greater than
$j(\min (\Omega ))$
to be greater than
 $0$
.
$0$
.
We now construct a
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence
![]() $\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , ~ i(\alpha ) \leq i < \theta \rangle $
. We will maintain the requirement that, for all
$\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma , ~ i(\alpha ) \leq i < \theta \rangle $
. We will maintain the requirement that, for all
![]() $\alpha \in \Omega $
, we have
$\alpha \in \Omega $
, we have
![]() $i(\alpha ) = j(\alpha )$
and
$i(\alpha ) = j(\alpha )$
and
![]() $\operatorname {\mathrm {acc}}(D_{\alpha }) \subseteq \operatorname {\mathrm {acc}}(C_{\alpha , i(\alpha )})$
.
$\operatorname {\mathrm {acc}}(D_{\alpha }) \subseteq \operatorname {\mathrm {acc}}(C_{\alpha , i(\alpha )})$
.
As a base case, if
![]() $\beta = \min (\Gamma )$
, then by Claim 4.13.1(3), we have
$\beta = \min (\Gamma )$
, then by Claim 4.13.1(3), we have
![]() $\operatorname {\mathrm {otp}}(D_{\beta }) = \omega $
. Set
$\operatorname {\mathrm {otp}}(D_{\beta }) = \omega $
. Set
![]() $i(\beta ):=0$
, and let
$i(\beta ):=0$
, and let
![]() $C_{\beta , i} := D_{\beta }$
for all
$C_{\beta , i} := D_{\beta }$
for all
![]() $i<\theta $
. Note that if
$i<\theta $
. Note that if
![]() $\beta \in \Omega $
, then by Claim 4.13.1(5), indeed
$\beta \in \Omega $
, then by Claim 4.13.1(5), indeed
![]() $i(\beta )=j(\beta )$
.
$i(\beta )=j(\beta )$
.
Suppose now that
![]() $\beta \in \Gamma \setminus \{\min (\Gamma )\}$
and we have defined
$\beta \in \Gamma \setminus \{\min (\Gamma )\}$
and we have defined
![]() $\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma \cap \beta , ~ i(\alpha ) \leq i < \theta \rangle $
satisfying all relevant instances of Clauses (2) and (3) of Definition 4.2 as well as our recursive requirement. The construction breaks into a number of different cases based on the identity of
$\langle C_{\alpha , i} \mathrel {|} \alpha \in \Gamma \cap \beta , ~ i(\alpha ) \leq i < \theta \rangle $
satisfying all relevant instances of Clauses (2) and (3) of Definition 4.2 as well as our recursive requirement. The construction breaks into a number of different cases based on the identity of
![]() $\beta $
. In all cases, the verification that our sequence satisfies our recursive requirement and Clauses (2) and (3) of Definition 4.2 at
$\beta $
. In all cases, the verification that our sequence satisfies our recursive requirement and Clauses (2) and (3) of Definition 4.2 at
![]() $\beta $
is routine and therefore largely left to the reader.
$\beta $
is routine and therefore largely left to the reader.
-
Case 1:
 $\beta \in \Gamma \setminus \Omega $
. In particular, we have
$\beta \in \Gamma \setminus \Omega $
. In particular, we have
 $\operatorname {\mathrm {cf}}(\beta ) < \theta $
. We now split into subcases depending on the behavior of
$\operatorname {\mathrm {cf}}(\beta ) < \theta $
. We now split into subcases depending on the behavior of
 $\Gamma \cap \beta $
.
$\Gamma \cap \beta $
. -
Case 1a:
 $\sup (\Gamma \cap \beta ) < \beta $
and
$\sup (\Gamma \cap \beta ) < \beta $
and
 $\max (\Gamma \cap \beta )$
exists. Let
$\max (\Gamma \cap \beta )$
exists. Let
 $\alpha := \max (\Gamma \cap \beta )$
. By Claim 4.13.1(3), we know that
$\alpha := \max (\Gamma \cap \beta )$
. By Claim 4.13.1(3), we know that
 $D^-_{\beta } := D_{\beta } \setminus \alpha $
has order type
$D^-_{\beta } := D_{\beta } \setminus \alpha $
has order type
 $\omega $
. Let
$\omega $
. Let
 $i(\beta ) := i(\alpha )$
and, for all
$i(\beta ) := i(\alpha )$
and, for all
 $i \in [i(\beta ), \theta )$
, let
$i \in [i(\beta ), \theta )$
, let
 $C_{\beta , i} = C_{\alpha , i} \cup \{\alpha \} \cup D^-_{\beta }$
.
$C_{\beta , i} = C_{\alpha , i} \cup \{\alpha \} \cup D^-_{\beta }$
. -
Case 1b:
 $\sup (\Gamma \cap \beta ) < \beta $
but
$\sup (\Gamma \cap \beta ) < \beta $
but
 $\max (\Gamma \cap \beta )$
does not exist. Let
$\max (\Gamma \cap \beta )$
does not exist. Let
 $\alpha := \sup (\Gamma \cap \beta )$
. As in Case (1a), we know that
$\alpha := \sup (\Gamma \cap \beta )$
. As in Case (1a), we know that
 $D^-_{\beta } := D_{\beta } \setminus \alpha $
has order type
$D^-_{\beta } := D_{\beta } \setminus \alpha $
has order type
 $\omega $
. Since
$\omega $
. Since
 $\alpha \notin \Gamma $
, it follows that
$\alpha \notin \Gamma $
, it follows that
 $\alpha \in E^{\kappa }_{\theta }$
. Since
$\alpha \in E^{\kappa }_{\theta }$
. Since
 $\operatorname {\mathrm {cf}}(\beta ) < \theta $
, we know that
$\operatorname {\mathrm {cf}}(\beta ) < \theta $
, we know that
 $\theta> \omega $
, and hence
$\theta> \omega $
, and hence
 $\operatorname {\mathrm {acc}}(D_{\alpha })$
is unbounded in
$\operatorname {\mathrm {acc}}(D_{\alpha })$
is unbounded in
 $\alpha $
. Let
$\alpha $
. Let
 $\langle \alpha _i \mathrel {|} i < \theta \rangle $
be a strictly increasing sequence of elements of
$\langle \alpha _i \mathrel {|} i < \theta \rangle $
be a strictly increasing sequence of elements of
 $\operatorname {\mathrm {acc}}(D_{\alpha })$
converging to
$\operatorname {\mathrm {acc}}(D_{\alpha })$
converging to
 $\alpha $
. As
$\alpha $
. As
 $\alpha \in E^{\kappa }_{\theta }\subseteq \Delta $
, it follows from Claim 4.13.1(2) that, for all
$\alpha \in E^{\kappa }_{\theta }\subseteq \Delta $
, it follows from Claim 4.13.1(2) that, for all
 $i<\theta $
,
$i<\theta $
,
 $\alpha _i\in \Omega \subseteq \Gamma $
and
$\alpha _i\in \Omega \subseteq \Gamma $
and
 $j(\alpha _i)=j(\alpha )$
. So, by the fact that our construction thus far satisfies all of our requirements, we know that, for all
$j(\alpha _i)=j(\alpha )$
. So, by the fact that our construction thus far satisfies all of our requirements, we know that, for all
 $i < \theta $
, we have
$i < \theta $
, we have
 $i(\alpha _i) = j(\alpha )$
and
$i(\alpha _i) = j(\alpha )$
and
 $\operatorname {\mathrm {acc}}(D_{\alpha }) \cap \alpha _i = \operatorname {\mathrm {acc}}(D_{\alpha _i})\subseteq \operatorname {\mathrm {acc}}(C_{\alpha _i, j(\alpha )})$
. Set
$\operatorname {\mathrm {acc}}(D_{\alpha }) \cap \alpha _i = \operatorname {\mathrm {acc}}(D_{\alpha _i})\subseteq \operatorname {\mathrm {acc}}(C_{\alpha _i, j(\alpha )})$
. Set
 $i(\beta ):= j(\alpha )$
and
$i(\beta ):= j(\alpha )$
and
 $C_{\beta , i} := C_{\alpha _i, i} \cup \{\alpha _i\} \cup D^-_{\beta }$
for all
$C_{\beta , i} := C_{\alpha _i, i} \cup \{\alpha _i\} \cup D^-_{\beta }$
for all
 $i\in [i(\beta ),\theta )$
.
$i\in [i(\beta ),\theta )$
. -
Case 1c:
 $\sup (\Gamma \cap \beta ) = \beta $
. In this case, let
$\sup (\Gamma \cap \beta ) = \beta $
. In this case, let
 $\langle \alpha _{\eta } \mathrel {|} \eta < \operatorname {\mathrm {cf}}(\beta ) \rangle $
be an increasing sequence of elements of
$\langle \alpha _{\eta } \mathrel {|} \eta < \operatorname {\mathrm {cf}}(\beta ) \rangle $
be an increasing sequence of elements of
 $\Gamma $
converging to
$\Gamma $
converging to
 $\beta $
. Let
$\beta $
. Let
 $i(\beta )$
be the least ordinal
$i(\beta )$
be the least ordinal
 $i < \theta $
such that, for all
$i < \theta $
such that, for all
 $\eta < \xi < \operatorname {\mathrm {cf}}(\beta )$
, we have
$\eta < \xi < \operatorname {\mathrm {cf}}(\beta )$
, we have
 $i(\alpha _{\eta }), i(\alpha _{\xi }) \leq i$
and
$i(\alpha _{\eta }), i(\alpha _{\xi }) \leq i$
and
 $\alpha _{\eta } \in \operatorname {\mathrm {acc}}(C_{\alpha _{\xi }, i})$
. Such an ordinal exists because
$\alpha _{\eta } \in \operatorname {\mathrm {acc}}(C_{\alpha _{\xi }, i})$
. Such an ordinal exists because
 $\operatorname {\mathrm {cf}}(\beta ) < \theta $
and our sequence so far satisfies Clauses (2) and (3) of Definition 4.2. Then, for all
$\operatorname {\mathrm {cf}}(\beta ) < \theta $
and our sequence so far satisfies Clauses (2) and (3) of Definition 4.2. Then, for all
 $i \in [i(\beta ), \theta )$
, let
$i \in [i(\beta ), \theta )$
, let
 $C_{\beta , i} = \bigcup _{\eta < \operatorname {\mathrm {cf}}(\beta )} C_{\alpha _{\eta }, i}$
.
$C_{\beta , i} = \bigcup _{\eta < \operatorname {\mathrm {cf}}(\beta )} C_{\alpha _{\eta }, i}$
. -
Case 2:
 $\beta \in \Omega $
. In this case, we are required to set
$\beta \in \Omega $
. In this case, we are required to set
 $i(\beta ) := j(\beta )$
. We again split into subcases depending on the behavior of
$i(\beta ) := j(\beta )$
. We again split into subcases depending on the behavior of
 $\Gamma \cap \beta $
and
$\Gamma \cap \beta $
and
 $\operatorname {\mathrm {acc}}(D_{\beta })$
.
$\operatorname {\mathrm {acc}}(D_{\beta })$
. -
Case 2a:
 $\sup (\Gamma \cap \beta ) < \beta $
and
$\sup (\Gamma \cap \beta ) < \beta $
and
 $\max (\Gamma \cap \beta )$
exists. Let
$\max (\Gamma \cap \beta )$
exists. Let
 $\alpha := \max (\Gamma \cap \beta )$
. As in Case (1a), we know that
$\alpha := \max (\Gamma \cap \beta )$
. As in Case (1a), we know that
 $D^-_{\beta } := D_{\beta } \setminus \alpha $
has order type
$D^-_{\beta } := D_{\beta } \setminus \alpha $
has order type
 $\omega $
.
$\omega $
.
 $\blacktriangleright $
If
$\blacktriangleright $
If
 $\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })$
, then
$\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })$
, then
 $i(\alpha )=j(\alpha )=j(\beta )=i(\beta )$
, so we let
$i(\alpha )=j(\alpha )=j(\beta )=i(\beta )$
, so we let
 $C_{\beta , i} := C_{\alpha , i} \cup \{\alpha \} \cup D^-_{\beta }$
for all
$C_{\beta , i} := C_{\alpha , i} \cup \{\alpha \} \cup D^-_{\beta }$
for all
 $i\in [i(\beta ),\theta )$
. Note that so we have satisfied our recursive hypothesis.
$i\in [i(\beta ),\theta )$
. Note that so we have satisfied our recursive hypothesis. $$\begin{align*}\operatorname{\mathrm{acc}}(D_{\beta}) = \operatorname{\mathrm{acc}}(D_{\alpha}) \cup \{\alpha\} \subseteq \operatorname{\mathrm{acc}}(C_{\alpha, i(\alpha)}) \cup \{\alpha\} \subseteq \operatorname{\mathrm{acc}}(C_{\beta, i(\beta)}), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{acc}}(D_{\beta}) = \operatorname{\mathrm{acc}}(D_{\alpha}) \cup \{\alpha\} \subseteq \operatorname{\mathrm{acc}}(C_{\alpha, i(\alpha)}) \cup \{\alpha\} \subseteq \operatorname{\mathrm{acc}}(C_{\beta, i(\beta)}), \end{align*}$$
 $\blacktriangleright $
If
$\blacktriangleright $
If
 $\operatorname {\mathrm {acc}}(D_{\beta }) \neq \emptyset $
but
$\operatorname {\mathrm {acc}}(D_{\beta }) \neq \emptyset $
but
 $\alpha>\max (\operatorname {\mathrm {acc}}(D_{\beta }))$
, then let
$\alpha>\max (\operatorname {\mathrm {acc}}(D_{\beta }))$
, then let
 $\alpha ^* := \max (\operatorname {\mathrm {acc}}(D_{\beta }))$
and let
$\alpha ^* := \max (\operatorname {\mathrm {acc}}(D_{\beta }))$
and let
 $i^*\in [i(\alpha ),\theta )$
be least such that
$i^*\in [i(\alpha ),\theta )$
be least such that
 $\alpha ^* \in \operatorname {\mathrm {acc}}(C_{\alpha , i^*})$
. Note that
$\alpha ^* \in \operatorname {\mathrm {acc}}(C_{\alpha , i^*})$
. Note that
 $i(\beta )=i(\alpha ^*)\le i^*$
. Let
$i(\beta )=i(\alpha ^*)\le i^*$
. Let
 $C_{\beta , i} := C_{\alpha ^*, i} \cup \{\alpha ^*\} \cup D^-_{\beta }$
for all
$C_{\beta , i} := C_{\alpha ^*, i} \cup \{\alpha ^*\} \cup D^-_{\beta }$
for all
 $i\in [i(\beta ),i^*)$
, and let
$i\in [i(\beta ),i^*)$
, and let
 $C_{\beta , i} := C_{\alpha , i} \cup \{\alpha \} \cup D^-_{\beta }$
for all
$C_{\beta , i} := C_{\alpha , i} \cup \{\alpha \} \cup D^-_{\beta }$
for all
 $i\in [i^*,\theta )$
.
$i\in [i^*,\theta )$
.Note that we have satisfied our recursive hypothesis.
 $\blacktriangleright $
If
$\blacktriangleright $
If
 $\operatorname {\mathrm {acc}}(D_{\beta })=\emptyset $
, then let
$\operatorname {\mathrm {acc}}(D_{\beta })=\emptyset $
, then let
 $C_{\beta ,i}:=D_{\beta }^-$
for all
$C_{\beta ,i}:=D_{\beta }^-$
for all
 $i\in [i(\beta ),i(\alpha ))$
, and let
$i\in [i(\beta ),i(\alpha ))$
, and let
 $C_{\beta , i} := C_{\alpha , i} \cup \{\alpha \} \cup D^-_{\beta }$
for all
$C_{\beta , i} := C_{\alpha , i} \cup \{\alpha \} \cup D^-_{\beta }$
for all
 $i\in [\max \{i(\beta ),i(\alpha )\},\theta )$
.
$i\in [\max \{i(\beta ),i(\alpha )\},\theta )$
. -
Case 2b:
 $\sup (\Gamma \cap \beta ) < \beta $
but
$\sup (\Gamma \cap \beta ) < \beta $
but
 $\max (\Gamma \cap \beta )$
does not exist. Let
$\max (\Gamma \cap \beta )$
does not exist. Let
 $\alpha := \sup (\Gamma \cap \beta )$
. Once again, it follows that
$\alpha := \sup (\Gamma \cap \beta )$
. Once again, it follows that
 $D^-_{\beta } := D_{\beta } \setminus \alpha $
has order type
$D^-_{\beta } := D_{\beta } \setminus \alpha $
has order type
 $\omega $
. As in Case (1b), we have
$\omega $
. As in Case (1b), we have
 $\alpha \in E^{\kappa }_{\theta }$
, and, for all
$\alpha \in E^{\kappa }_{\theta }$
, and, for all
 $\bar \alpha \in \operatorname {\mathrm {acc}}(D_{\alpha })$
, we have
$\bar \alpha \in \operatorname {\mathrm {acc}}(D_{\alpha })$
, we have
 $\bar \alpha \in \Omega $
and
$\bar \alpha \in \Omega $
and
 $j(\bar \alpha )=j(\alpha )$
. Let
$j(\bar \alpha )=j(\alpha )$
. Let
 $\alpha ^*:=\max (\operatorname {\mathrm {acc}}(D_{\beta }))$
if
$\alpha ^*:=\max (\operatorname {\mathrm {acc}}(D_{\beta }))$
if
 $\operatorname {\mathrm {acc}}(D_{\beta }) \neq \emptyset $
, and
$\operatorname {\mathrm {acc}}(D_{\beta }) \neq \emptyset $
, and
 $\alpha ^* := \min (\Gamma )$
otherwise. In either case, note that
$\alpha ^* := \min (\Gamma )$
otherwise. In either case, note that
 $\alpha ^* < \alpha $
and
$\alpha ^* < \alpha $
and
 $i(\alpha ^*) \le i(\beta )$
.
$i(\alpha ^*) \le i(\beta )$
.Our construction now depends on whether or not
 $\theta = \omega $
.
$\theta = \omega $
. $\blacktriangleright $
If
$\blacktriangleright $
If
 $\theta = \omega $
, then let
$\theta = \omega $
, then let
 $\langle \alpha _n \mathrel {|} n < \omega \rangle $
be a strictly increasing sequence of elements of
$\langle \alpha _n \mathrel {|} n < \omega \rangle $
be a strictly increasing sequence of elements of
 $\Gamma \cap \alpha $
converging to
$\Gamma \cap \alpha $
converging to
 $\alpha $
such that
$\alpha $
such that
 $\alpha _0 = \alpha ^*$
. Let
$\alpha _0 = \alpha ^*$
. Let
 $\langle i_n \mathrel {|} n < \omega \rangle $
be a strictly increasing sequence of natural numbers such that, for all
$\langle i_n \mathrel {|} n < \omega \rangle $
be a strictly increasing sequence of natural numbers such that, for all
 $n < \omega $
,
$n < \omega $
,
 $\max \{i(\alpha _m)\mathrel {|} m\le n\}\le i_n$
and
$\max \{i(\alpha _m)\mathrel {|} m\le n\}\le i_n$
and
 $\{\alpha _m \mathrel {|} m<n\}\subseteq \operatorname {\mathrm {acc}}(C_{\alpha _n, i_n})$
.
$\{\alpha _m \mathrel {|} m<n\}\subseteq \operatorname {\mathrm {acc}}(C_{\alpha _n, i_n})$
.Finally, for all
 $i \in [i(\beta ), \omega )$
, let
$i \in [i(\beta ), \omega )$
, let
 $n < \omega $
be such that
$n < \omega $
be such that
 $i_n \leq i < i_{n+1}$
, and set
$i_n \leq i < i_{n+1}$
, and set
 $C_{\beta , i} := C_{\alpha _n, i} \cup \{\alpha _n\} \cup D^-_{\beta }$
.
$C_{\beta , i} := C_{\alpha _n, i} \cup \{\alpha _n\} \cup D^-_{\beta }$
. $\blacktriangleright $
If
$\blacktriangleright $
If
 $\theta> \omega $
, then let
$\theta> \omega $
, then let
 $\langle \alpha _i \mathrel {|} i < \theta \rangle $
be a strictly increasing sequence of elements of
$\langle \alpha _i \mathrel {|} i < \theta \rangle $
be a strictly increasing sequence of elements of
 $\operatorname {\mathrm {acc}}(D_{\alpha })$
converging to
$\operatorname {\mathrm {acc}}(D_{\alpha })$
converging to
 $\alpha $
such that
$\alpha $
such that
 $\alpha _0> \alpha ^*$
. As noted earlier, we have
$\alpha _0> \alpha ^*$
. As noted earlier, we have
 $i(\alpha _i) = j(\alpha )$
. Let
$i(\alpha _i) = j(\alpha )$
. Let
 $i^*\in [j(\alpha ),\theta )$
be least such that
$i^*\in [j(\alpha ),\theta )$
be least such that
 $\alpha ^* \in \operatorname {\mathrm {acc}}(C_{\alpha _0, i^*})$
. In particular, for all
$\alpha ^* \in \operatorname {\mathrm {acc}}(C_{\alpha _0, i^*})$
. In particular, for all
 $i \in [i^*, \theta )$
, we have
$i \in [i^*, \theta )$
, we have
 $\alpha ^* \in \operatorname {\mathrm {acc}}(C_{\alpha _i, i})$
, so that
$\alpha ^* \in \operatorname {\mathrm {acc}}(C_{\alpha _i, i})$
, so that
 $\operatorname {\mathrm {acc}}(D_{\beta })\subseteq \operatorname {\mathrm {acc}}(C_{\alpha _i, i})$
.
$\operatorname {\mathrm {acc}}(D_{\beta })\subseteq \operatorname {\mathrm {acc}}(C_{\alpha _i, i})$
.Now, let
 $C_{\beta , i} := C_{\alpha ^*, i} \cup \{\alpha ^*\} \cup D^-_{\beta }$
for all
$C_{\beta , i} := C_{\alpha ^*, i} \cup \{\alpha ^*\} \cup D^-_{\beta }$
for all
 $i\in [i(\beta ),i^*)$
, and let
$i\in [i(\beta ),i^*)$
, and let
 $C_{\beta , i} := C_{\alpha _i, i} \cup \{\alpha _i\} \cup D^-_{\beta }$
for all
$C_{\beta , i} := C_{\alpha _i, i} \cup \{\alpha _i\} \cup D^-_{\beta }$
for all
 $i\in [i^*,\theta )$
.
$i\in [i^*,\theta )$
. -
Case 2c:
 $\sup (\Gamma \cap \beta ) = \beta $
but
$\sup (\Gamma \cap \beta ) = \beta $
but
 $\sup (\operatorname {\mathrm {acc}}(D_{\beta })) < \beta $
. In this case,
$\sup (\operatorname {\mathrm {acc}}(D_{\beta })) < \beta $
. In this case,
 $\operatorname {\mathrm {otp}}(D_{\beta }\setminus \sup (\operatorname {\mathrm {acc}}(D_{\beta })))=\omega $
. Let
$\operatorname {\mathrm {otp}}(D_{\beta }\setminus \sup (\operatorname {\mathrm {acc}}(D_{\beta })))=\omega $
. Let
 $\alpha ^*:=\max (\operatorname {\mathrm {acc}}(D_{\beta }))$
if
$\alpha ^*:=\max (\operatorname {\mathrm {acc}}(D_{\beta }))$
if
 $\operatorname {\mathrm {acc}}(D_{\beta }) \neq \emptyset $
, and
$\operatorname {\mathrm {acc}}(D_{\beta }) \neq \emptyset $
, and
 $\alpha ^* := \min (\Gamma )$
otherwise. In either case,
$\alpha ^* := \min (\Gamma )$
otherwise. In either case,
 $\alpha ^* < \alpha $
and
$\alpha ^* < \alpha $
and
 $i(\alpha ^*) \le i(\beta )$
. Let
$i(\alpha ^*) \le i(\beta )$
. Let
 $\langle \alpha _n \mathrel {|} n < \omega \rangle $
be an increasing sequence of elements of
$\langle \alpha _n \mathrel {|} n < \omega \rangle $
be an increasing sequence of elements of
 $\Gamma $
converging to
$\Gamma $
converging to
 $\beta $
with
$\beta $
with
 $\alpha _0 := \alpha ^*$
. Fix an increasing sequence
$\alpha _0 := \alpha ^*$
. Fix an increasing sequence
 $\langle i_n \mathrel {|} n < \omega \rangle $
of ordinals below
$\langle i_n \mathrel {|} n < \omega \rangle $
of ordinals below
 $\theta $
such that for all
$\theta $
such that for all
 $n < \omega $
,
$n < \omega $
,
 $\max \{i(\alpha _m)\mathrel {|} m\le n\}\le i_n$
and
$\max \{i(\alpha _m)\mathrel {|} m\le n\}\le i_n$
and
 $\{\alpha _m \mathrel {|} m<n\}\subseteq \operatorname {\mathrm {acc}}(C_{\alpha _n, i_n})$
.
$\{\alpha _m \mathrel {|} m<n\}\subseteq \operatorname {\mathrm {acc}}(C_{\alpha _n, i_n})$
.Finally, fix
 $i\in [i(\beta ),\theta )$
. If there is
$i\in [i(\beta ),\theta )$
. If there is
 $k < \omega $
such that
$k < \omega $
such that
 $i_k \leq i < i_{k+1}$
, then set
$i_k \leq i < i_{k+1}$
, then set
 $C_{\beta , i} := C_{\alpha _k, i} \cup \{\alpha _n \mathrel {|} k \leq n < \omega \}$
for this unique k. Otherwise, set
$C_{\beta , i} := C_{\alpha _k, i} \cup \{\alpha _n \mathrel {|} k \leq n < \omega \}$
for this unique k. Otherwise, set
 $C_{\beta , i} := \bigcup _{n < \omega } C_{\alpha _n, i}$
.
$C_{\beta , i} := \bigcup _{n < \omega } C_{\alpha _n, i}$
. -
Case 2d:
 $\sup (\operatorname {\mathrm {acc}}(D_{\beta })) = \beta $
. Note that, for all
$\sup (\operatorname {\mathrm {acc}}(D_{\beta })) = \beta $
. Note that, for all
 $\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })$
, we have
$\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })$
, we have
 $\alpha \in \Omega $
,
$\alpha \in \Omega $
,
 $i(\alpha ) = i(\beta )$
, and
$i(\alpha ) = i(\beta )$
, and
 $\operatorname {\mathrm {acc}}(D_{\beta }) \cap \alpha = \operatorname {\mathrm {acc}}(D_{\alpha }) \subseteq C_{\alpha , i(\alpha )}$
. Therefore, for all
$\operatorname {\mathrm {acc}}(D_{\beta }) \cap \alpha = \operatorname {\mathrm {acc}}(D_{\alpha }) \subseteq C_{\alpha , i(\alpha )}$
. Therefore, for all
 $i\in [i(\beta ),\theta )$
, we can simply set
$i\in [i(\beta ),\theta )$
, we can simply set
 $C_{\beta , i} := \bigcup _{\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })} C_{\alpha , i}$
.
$C_{\beta , i} := \bigcup _{\alpha \in \operatorname {\mathrm {acc}}(D_{\beta })} C_{\alpha , i}$
.
Our construction has yielded a matrix satisfying Clauses (1)–(3) of Definition 4.2 and such that
![]() $\Gamma \cap T = \emptyset $
. It remains to verify Clause (4) of Definition 4.2. Towards a contradiction, suppose that D is a club in
$\Gamma \cap T = \emptyset $
. It remains to verify Clause (4) of Definition 4.2. Towards a contradiction, suppose that D is a club in
![]() $\kappa $
satisfying that, for every
$\kappa $
satisfying that, for every
![]() $\alpha \in \operatorname {\mathrm {acc}}(D) \cap \Gamma $
, there exists
$\alpha \in \operatorname {\mathrm {acc}}(D) \cap \Gamma $
, there exists
![]() $i<\theta $
such that
$i<\theta $
such that
![]() $D\cap \alpha \neq C_{\alpha ,i}$
. Fix
$D\cap \alpha \neq C_{\alpha ,i}$
. Fix
![]() $i<\theta $
for which
$i<\theta $
for which
![]() $G:=\{\gamma \in \Gamma \mathrel {|} D\cap \gamma =C_{\gamma ,i}\}$
is stationary. Recalling Claim 4.13.1(4), let us now fix
$G:=\{\gamma \in \Gamma \mathrel {|} D\cap \gamma =C_{\gamma ,i}\}$
is stationary. Recalling Claim 4.13.1(4), let us now fix
![]() $\beta \in \Gamma _{i+1}\cap \operatorname {\mathrm {acc}}(D)$
. Pick
$\beta \in \Gamma _{i+1}\cap \operatorname {\mathrm {acc}}(D)$
. Pick
![]() $\gamma \in G$
above
$\gamma \in G$
above
![]() $\beta $
. Then
$\beta $
. Then
![]() $\beta \in \operatorname {\mathrm {acc}}(D\cap \gamma )=\operatorname {\mathrm {acc}}(C_{\gamma ,i})$
, so
$\beta \in \operatorname {\mathrm {acc}}(D\cap \gamma )=\operatorname {\mathrm {acc}}(C_{\gamma ,i})$
, so
![]() $i(\beta )\le i$
, contradicting the fact that
$i(\beta )\le i$
, contradicting the fact that
![]() $i(\beta )=j(\beta )=i+1$
.
$i(\beta )=j(\beta )=i+1$
.
Corollary 4.14.
![]() $(\aleph _{\omega +1},\aleph _{\omega })\twoheadrightarrow (\aleph _1,\aleph _0)$
is compatible with
$(\aleph _{\omega +1},\aleph _{\omega })\twoheadrightarrow (\aleph _1,\aleph _0)$
is compatible with
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}} (\aleph _{\omega +1},\aleph _{\omega +1}, \theta ,\aleph _{\omega })$
holding for every infinite cardinal
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}} (\aleph _{\omega +1},\aleph _{\omega +1}, \theta ,\aleph _{\omega })$
holding for every infinite cardinal
![]() $\theta <\aleph _{\omega }$
.
$\theta <\aleph _{\omega }$
.
Proof Starting with a ground model in which
![]() $(\aleph _{\omega +1},\aleph _{\omega })\twoheadrightarrow (\aleph _1,\aleph _0)$
holds, one can add a
$(\aleph _{\omega +1},\aleph _{\omega })\twoheadrightarrow (\aleph _1,\aleph _0)$
holds, one can add a
![]() $\square (\aleph _{\omega +1})$
-sequence via an
$\square (\aleph _{\omega +1})$
-sequence via an
![]() $\aleph _{\omega +1}$
-strategically closed forcing, hence preserving the principle
$\aleph _{\omega +1}$
-strategically closed forcing, hence preserving the principle
![]() $(\aleph _{\omega +1},\aleph _{\omega })\twoheadrightarrow (\aleph _1,\aleph _0)$
. By Theorems 4.4 and 4.13, in the extension,
$(\aleph _{\omega +1},\aleph _{\omega })\twoheadrightarrow (\aleph _1,\aleph _0)$
. By Theorems 4.4 and 4.13, in the extension,
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\aleph _{\omega +1},\aleph _{\omega +1}, \theta ,\aleph _{\omega })$
holds for every infinite cardinal
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\aleph _{\omega +1},\aleph _{\omega +1}, \theta ,\aleph _{\omega })$
holds for every infinite cardinal
![]() $\theta <\aleph _{\omega }$
.
$\theta <\aleph _{\omega }$
.
By Theorem 3.34, for any
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
, there exists a
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
, there exists a
![]() $\theta ^+$
-directed closed,
$\theta ^+$
-directed closed,
![]() $\kappa $
-strategically closed forcing notion that introduces a somewhere-closed witness to
$\kappa $
-strategically closed forcing notion that introduces a somewhere-closed witness to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )$
. In order to force a fully closed witness, it seems that we must decrease the degree of closure of the poset by one cardinal. The next theorem forms Clause (2) of Theorem C.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )$
. In order to force a fully closed witness, it seems that we must decrease the degree of closure of the poset by one cardinal. The next theorem forms Clause (2) of Theorem C.
Theorem 4.15. Suppose that
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. Then there exists a
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
. Then there exists a
![]() $\theta $
-directed closed,
$\theta $
-directed closed,
![]() $\kappa $
-strategically closed forcing notion that introduces a closed witness
$\kappa $
-strategically closed forcing notion that introduces a closed witness
![]() $c:[\kappa ]^2\rightarrow \theta $
to
$c:[\kappa ]^2\rightarrow \theta $
to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )$
for which
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )$
for which
![]() $\partial (c)$
is stationary.
$\partial (c)$
is stationary.
Proof By [Reference Lambie-Hanson17, Section 7], there is a
![]() $\theta $
-directed closed,
$\theta $
-directed closed,
![]() $\kappa $
-strategically closed forcing notion that adds an
$\kappa $
-strategically closed forcing notion that adds an
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence and therefore, by Theorem 4.4, it adds a closed witness c to
$\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence and therefore, by Theorem 4.4, it adds a closed witness c to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )$
. However, unless
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )$
. However, unless
![]() $\theta =\omega $
, it is unclear whether
$\theta =\omega $
, it is unclear whether
![]() $\partial (c)$
can be made to be stationary in this case. Thus, instead, we appeal to the forcing
$\partial (c)$
can be made to be stationary in this case. Thus, instead, we appeal to the forcing
![]() $\mathbb P(\kappa ,\theta )$
from [Reference Lambie-Hanson and Rinot21, Section 3.3]. This is a
$\mathbb P(\kappa ,\theta )$
from [Reference Lambie-Hanson and Rinot21, Section 3.3]. This is a
![]() $\theta $
-directed closed,
$\theta $
-directed closed,
![]() $\kappa $
-strategically closed forcing notion that introduces a witness
$\kappa $
-strategically closed forcing notion that introduces a witness
![]() $\vec C=\langle C_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
to
$\vec C=\langle C_{\alpha }\mathrel {|} \alpha <\kappa \rangle $
to
![]() $\operatorname {\mathrm {P}}^-(\kappa ,2, {\sqsubseteq _{\theta }},1,\{\kappa \},2,\sigma )$
for every
$\operatorname {\mathrm {P}}^-(\kappa ,2, {\sqsubseteq _{\theta }},1,\{\kappa \},2,\sigma )$
for every
![]() $\sigma <\kappa $
. Now, utilizing the instance
$\sigma <\kappa $
. Now, utilizing the instance
![]() $\sigma :=\theta $
, the proof of [Reference Lambie-Hanson16, Theorem 4.1] makes it clear that the set
$\sigma :=\theta $
, the proof of [Reference Lambie-Hanson16, Theorem 4.1] makes it clear that the set
![]() $\{\alpha \in E^{\kappa }_{\theta }\mathrel {|} \exists \eta < \alpha [\operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )=\theta ]\}$
is stationary. Fix some
$\{\alpha \in E^{\kappa }_{\theta }\mathrel {|} \exists \eta < \alpha [\operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )=\theta ]\}$
is stationary. Fix some
![]() $\eta <\kappa $
for which
$\eta <\kappa $
for which
![]() $T:=\{\alpha \in E^{\kappa }_{\theta }\mathrel {|} \operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )=\theta \}$
is stationary. Note that, by the
$T:=\{\alpha \in E^{\kappa }_{\theta }\mathrel {|} \operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )=\theta \}$
is stationary. Note that, by the
![]() $\sqsubseteq _{\theta }$
-coherence of
$\sqsubseteq _{\theta }$
-coherence of
![]() $\vec C$
, the set
$\vec C$
, the set
![]() $\Gamma :=\{\alpha \in \operatorname {\mathrm {acc}}(\kappa )\mathrel {|} \forall \bar \alpha \in \operatorname {\mathrm {acc}}(C_{\alpha })[C_{\bar \alpha }\sqsubseteq C_{\alpha }]\}$
covers
$\Gamma :=\{\alpha \in \operatorname {\mathrm {acc}}(\kappa )\mathrel {|} \forall \bar \alpha \in \operatorname {\mathrm {acc}}(C_{\alpha })[C_{\bar \alpha }\sqsubseteq C_{\alpha }]\}$
covers
![]() $E^{\kappa }_{\ge \theta }$
. Now, define a C-sequence
$E^{\kappa }_{\ge \theta }$
. Now, define a C-sequence
![]() $\vec {D} = \langle D_{\alpha } \mathrel {|} \alpha < \kappa \rangle $
as follows:
$\vec {D} = \langle D_{\alpha } \mathrel {|} \alpha < \kappa \rangle $
as follows:
-
• Let
 $D_0:=\emptyset $
.
$D_0:=\emptyset $
. -
• For every
 $\alpha <\kappa $
, let
$\alpha <\kappa $
, let
 $D_{\alpha +1}:=\{\alpha \}$
.
$D_{\alpha +1}:=\{\alpha \}$
. -
• For every
 $\alpha \in \operatorname {\mathrm {acc}}(\kappa )\setminus \Gamma $
, let
$\alpha \in \operatorname {\mathrm {acc}}(\kappa )\setminus \Gamma $
, let
 $D_{\alpha }$
be some club in
$D_{\alpha }$
be some club in
 $\alpha $
of order-type
$\alpha $
of order-type
 $\operatorname {\mathrm {cf}}(\alpha )$
such that
$\operatorname {\mathrm {cf}}(\alpha )$
such that
 $\operatorname {\mathrm {nacc}}(D_{\alpha })\subseteq \operatorname {\mathrm {nacc}}(\alpha )$
.
$\operatorname {\mathrm {nacc}}(D_{\alpha })\subseteq \operatorname {\mathrm {nacc}}(\alpha )$
. -
• For every
 $\alpha \in \Gamma $
such that
$\alpha \in \Gamma $
such that
 $\operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )\le \theta $
, let
$\operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )\le \theta $
, let
 $D_{\alpha }:=C_{\alpha }$
.
$D_{\alpha }:=C_{\alpha }$
. -
• For any other
 $\alpha $
, let
$\alpha $
, let
 $D_{\alpha }:=\{\beta \in C_{\alpha }\mathrel {|} \operatorname {\mathrm {otp}}((C_{\alpha }\setminus \eta )\cap \beta )>\theta \}$
.
$D_{\alpha }:=\{\beta \in C_{\alpha }\mathrel {|} \operatorname {\mathrm {otp}}((C_{\alpha }\setminus \eta )\cap \beta )>\theta \}$
.
Note that, for every
![]() $\alpha \in \kappa \setminus \Gamma $
,
$\alpha \in \kappa \setminus \Gamma $
,
![]() $\operatorname {\mathrm {otp}}(D_{\alpha })=\operatorname {\mathrm {cf}}(\alpha )<\theta $
, so
$\operatorname {\mathrm {otp}}(D_{\alpha })=\operatorname {\mathrm {cf}}(\alpha )<\theta $
, so
![]() $\operatorname {\mathrm {acc}}(D_{\alpha })\cap T=\emptyset $
.
$\operatorname {\mathrm {acc}}(D_{\alpha })\cap T=\emptyset $
.
Claim 4.15.1.
![]() $\vec D$
is a
$\vec D$
is a
![]() $\square (\kappa ,\sqsubseteq _{\theta })$
-sequence that avoids T.
$\square (\kappa ,\sqsubseteq _{\theta })$
-sequence that avoids T.
Proof As any
![]() $\sqsubseteq _{\theta }$
-coherent C-sequence that avoids a stationary set is a
$\sqsubseteq _{\theta }$
-coherent C-sequence that avoids a stationary set is a
![]() $\square (\kappa ,\sqsubseteq _{\theta })$
-sequence, we shall focus on verifying that
$\square (\kappa ,\sqsubseteq _{\theta })$
-sequence, we shall focus on verifying that
![]() $\vec D$
is
$\vec D$
is
![]() $\sqsubseteq _{\theta }$
-coherent and avoids T. By the definition of
$\sqsubseteq _{\theta }$
-coherent and avoids T. By the definition of
![]() $\vec D$
, it suffices to verify that for all
$\vec D$
, it suffices to verify that for all
![]() $\alpha \in \Gamma $
and
$\alpha \in \Gamma $
and
![]() $\bar \alpha \in \operatorname {\mathrm {acc}}(D_{\alpha })$
,
$\bar \alpha \in \operatorname {\mathrm {acc}}(D_{\alpha })$
,
![]() $D_{\bar \alpha }\sqsubseteq D_{\alpha }$
and
$D_{\bar \alpha }\sqsubseteq D_{\alpha }$
and
![]() $\bar \alpha \notin T$
. Now, given such a pair
$\bar \alpha \notin T$
. Now, given such a pair
![]() $\bar \alpha <\alpha $
, since
$\bar \alpha <\alpha $
, since
![]() $\alpha \in \Gamma $
, we infer that
$\alpha \in \Gamma $
, we infer that
![]() $C_{\bar \alpha }\sqsubseteq C_{\alpha }$
and
$C_{\bar \alpha }\sqsubseteq C_{\alpha }$
and
![]() $\bar \alpha \in \Gamma $
. We shall verify that
$\bar \alpha \in \Gamma $
. We shall verify that
![]() $D_{\bar \alpha }\sqsubseteq D_{\alpha }$
and that
$D_{\bar \alpha }\sqsubseteq D_{\alpha }$
and that
![]() $\bar \alpha \notin T$
.
$\bar \alpha \notin T$
.
-
▸ If
 $\operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )\le \theta $
, then
$\operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )\le \theta $
, then
 $\operatorname {\mathrm {otp}}(C_{\bar \alpha }\setminus \eta )<\theta $
, so
$\operatorname {\mathrm {otp}}(C_{\bar \alpha }\setminus \eta )<\theta $
, so
 $D_{\bar \alpha }=C_{\bar \alpha }\sqsubseteq C_{\alpha }=D_{\alpha }$
and
$D_{\bar \alpha }=C_{\bar \alpha }\sqsubseteq C_{\alpha }=D_{\alpha }$
and
 $\bar \alpha \notin T$
.
$\bar \alpha \notin T$
. -
▸ If
 $\operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )>\theta $
, then
$\operatorname {\mathrm {otp}}(C_{\alpha }\setminus \eta )>\theta $
, then
 $D_{\alpha }=\{\beta \in C_{\alpha }\mathrel {|} \operatorname {\mathrm {otp}}((C_{\alpha }\setminus \eta )\cap \beta )>\theta \}$
, and so, from
$D_{\alpha }=\{\beta \in C_{\alpha }\mathrel {|} \operatorname {\mathrm {otp}}((C_{\alpha }\setminus \eta )\cap \beta )>\theta \}$
, and so, from
 $\bar \alpha \in \operatorname {\mathrm {acc}}(D_{\alpha })$
and
$\bar \alpha \in \operatorname {\mathrm {acc}}(D_{\alpha })$
and
 $C_{\bar \alpha }=C_{\alpha }\cap \bar \alpha $
, it follows that
$C_{\bar \alpha }=C_{\alpha }\cap \bar \alpha $
, it follows that
 $\operatorname {\mathrm {otp}}(C_{\bar \alpha }\setminus \eta )>\theta $
, so again
$\operatorname {\mathrm {otp}}(C_{\bar \alpha }\setminus \eta )>\theta $
, so again
 $D_{\bar \alpha }\sqsubseteq D_{\alpha }$
and
$D_{\bar \alpha }\sqsubseteq D_{\alpha }$
and
 $\bar \alpha \notin T$
.
$\bar \alpha \notin T$
.
Now, by Theorem 4.13(2) and Lemma 3.2(3), there is a closed witness c to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )$
such that
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa ,\theta , \theta )$
such that
![]() $T\subseteq \partial (c)$
.
$T\subseteq \partial (c)$
.
It follows that there can be dramatic failures of monotonicity in the third coordinate of
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\ldots )$
.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\ldots )$
.
Corollary 4.16. Suppose that
![]() $\theta $
is an indestructible supercompact cardinal below
$\theta $
is an indestructible supercompact cardinal below
![]() $\kappa $
. Then there is a forcing extension in which all cofinalities
$\kappa $
. Then there is a forcing extension in which all cofinalities
![]() $\leq \kappa $
are preserved and all of the following hold:
$\leq \kappa $
are preserved and all of the following hold:
-
•
 $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,\kappa ,\theta ,\theta )$
holds and is witnessed by a closed coloring.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa ,\kappa ,\theta ,\theta )$
holds and is witnessed by a closed coloring. -
• For all
 $\theta '<\theta $
, no witness to
$\theta '<\theta $
, no witness to
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ',2)$
is subadditive of the second kind.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ',2)$
is subadditive of the second kind. -
• For all
 $\theta '<\theta $
such that
$\theta '<\theta $
such that
 $\kappa $
is not the successor of a singular cardinal of cofinality
$\kappa $
is not the successor of a singular cardinal of cofinality
 $\theta $
’, no witness to
$\theta $
’, no witness to
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ',2)$
is weakly subadditive of the first kind.
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ',2)$
is weakly subadditive of the first kind.
Proof By Theorem 4.15, there is a
![]() $\theta $
-directed closed,
$\theta $
-directed closed,
![]() $\kappa $
-strategically closed forcing notion
$\kappa $
-strategically closed forcing notion
![]() $\mathbb {P}$
that adds a closed witness to
$\mathbb {P}$
that adds a closed witness to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa , \theta , \theta )$
. Since
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , \kappa , \theta , \theta )$
. Since
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\theta $
-directed closed,
$\theta $
-directed closed,
![]() $\theta $
remains supercompact, so, we may appeal to Corollary 3.42.
$\theta $
remains supercompact, so, we may appeal to Corollary 3.42.
5 Successors of singular cardinals
Definition 5.1. Suppose that
![]() $\vec \lambda =\langle \lambda _j\mathrel {|} j<\nu \rangle $
is a sequence of infinite cardinals, each greater than
$\vec \lambda =\langle \lambda _j\mathrel {|} j<\nu \rangle $
is a sequence of infinite cardinals, each greater than
![]() $\nu $
. The principle
$\nu $
. The principle
![]() asserts the existence of a sequence
asserts the existence of a sequence
![]() $\langle X_{\alpha }\mathrel {|} \alpha <\sup (\vec \lambda )\rangle $
, and, for all
$\langle X_{\alpha }\mathrel {|} \alpha <\sup (\vec \lambda )\rangle $
, and, for all
![]() $j<\nu $
, a sequence
$j<\nu $
, a sequence
![]() $\vec {C}^j=\langle C_{\alpha }^j\mathrel {|} \alpha <\lambda _j^+\rangle $
such that:
$\vec {C}^j=\langle C_{\alpha }^j\mathrel {|} \alpha <\lambda _j^+\rangle $
such that:
-
• for all
 $j<\nu $
and
$j<\nu $
and
 $\alpha \in \operatorname {\mathrm {acc}}(\lambda _j^+)$
,
$\alpha \in \operatorname {\mathrm {acc}}(\lambda _j^+)$
,
 $C_{\alpha }^j$
is a club in
$C_{\alpha }^j$
is a club in
 $\alpha $
, and for all
$\alpha $
, and for all
 $\bar \alpha \in \operatorname {\mathrm {acc}}(C^j_{\alpha })$
,
$\bar \alpha \in \operatorname {\mathrm {acc}}(C^j_{\alpha })$
,-
–
 $C^j_{\bar \alpha }=C^j_{\alpha }\cap \bar \alpha $
;
$C^j_{\bar \alpha }=C^j_{\alpha }\cap \bar \alpha $
; -
–
 $X_{\bar \alpha }=X_{\alpha }\cap \bar \alpha $
, provided that
$X_{\bar \alpha }=X_{\alpha }\cap \bar \alpha $
, provided that
 $\alpha>\lambda _j$
;
$\alpha>\lambda _j$
;
-
-
• for arbitrary large regular cardinals
 $\Upsilon $
, for all
$\Upsilon $
, for all
 $p\in H_{\Upsilon }$
and
$p\in H_{\Upsilon }$
and
 $X\subseteq \sup (\vec \lambda )$
, there exists
$X\subseteq \sup (\vec \lambda )$
, there exists
 $N\prec H_{\Upsilon }$
such that
$N\prec H_{\Upsilon }$
such that-
–
 $p \in N$
;
$p \in N$
; -
–
 $|N| < \sup (\vec {\lambda })$
;
$|N| < \sup (\vec {\lambda })$
; -
– N is internally approachable of length
 $\nu ^+$
;
$\nu ^+$
; -
– for all sufficiently large
 $j < \nu $
, we have
$j < \nu $
, we have
 $X \cap \sup (N \cap \lambda _j^+) = X_{\sup (N \cap \lambda _j^+)}$
.
$X \cap \sup (N \cap \lambda _j^+) = X_{\sup (N \cap \lambda _j^+)}$
.
-
Remark 5.2. Note that, if
![]() holds for a sequence
holds for a sequence
![]() $\vec {\lambda } = \langle \lambda _j \mathrel {|} j < \nu \rangle $
, then
$\vec {\lambda } = \langle \lambda _j \mathrel {|} j < \nu \rangle $
, then
![]() $2^{\mu }\le \lambda $
for all
$2^{\mu }\le \lambda $
for all
![]() $\mu <\lambda $
. Moreover, as we will see in Claim 5.4.1,
$\mu <\lambda $
. Moreover, as we will see in Claim 5.4.1,
![]() $\square (\lambda _j^+)$
holds for all sufficiently large
$\square (\lambda _j^+)$
holds for all sufficiently large
![]() $j < \nu $
, as witnessed by the sequence
$j < \nu $
, as witnessed by the sequence
![]() $\vec {C^j}$
from the above definition.
$\vec {C^j}$
from the above definition.
We will soon show that
![]() entails certain instances of
entails certain instances of
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, \ldots )$
. We first need the following lemma.
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\lambda ^+, \ldots )$
. We first need the following lemma.
Lemma 5.3. Suppose that
![]() $\langle C_{\alpha } \mathrel {|} \alpha < \kappa \rangle $
is a
$\langle C_{\alpha } \mathrel {|} \alpha < \kappa \rangle $
is a
![]() $\square (\kappa )$
-sequence,
$\square (\kappa )$
-sequence,
![]() $\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
, and
$\theta \in \operatorname {\mathrm {Reg}}(\kappa )$
, and
![]() $h:\kappa \rightarrow \theta $
is any function such that:
$h:\kappa \rightarrow \theta $
is any function such that:
-
(1) for unboundedly many
 $i < \theta $
,
$i < \theta $
,
 $h^{-1}\{i\}$
is stationary;
$h^{-1}\{i\}$
is stationary; -
(2) for all
 $\alpha < \kappa $
and all
$\alpha < \kappa $
and all
 $\bar \alpha \in \operatorname {\mathrm {acc}}(C_{\alpha })$
, we have
$\bar \alpha \in \operatorname {\mathrm {acc}}(C_{\alpha })$
, we have
 $h(\bar \alpha ) = h(\alpha )$
.
$h(\bar \alpha ) = h(\alpha )$
.
Then there is a closed, subadditive witness c to
![]() $\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \sup (\operatorname {\mathrm {Reg}}(\kappa )))$
such that, for all
$\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \sup (\operatorname {\mathrm {Reg}}(\kappa )))$
such that, for all
![]() $(\alpha , \beta ) \in [\kappa ]^2$
with
$(\alpha , \beta ) \in [\kappa ]^2$
with
![]() $\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
, we have
$\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
, we have
![]() $c(\alpha , \beta ) \geq h(\alpha )$
.
$c(\alpha , \beta ) \geq h(\alpha )$
.
Proof By the proof of [Reference Lambie-Hanson and Lücke19, Theorem 3.4], the hypotheses of the lemma entail the existence of a
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence
$\square ^{\operatorname {\mathrm {ind}}}(\kappa , \theta )$
-sequence
![]() $\langle C_{\alpha , i} \mathrel {|} \alpha \in \operatorname {\mathrm {acc}}(\kappa ), ~ i(\alpha ) \leq i < \theta \rangle $
such that
$\langle C_{\alpha , i} \mathrel {|} \alpha \in \operatorname {\mathrm {acc}}(\kappa ), ~ i(\alpha ) \leq i < \theta \rangle $
such that
![]() $i(\alpha ) = h(\alpha )$
for all
$i(\alpha ) = h(\alpha )$
for all
![]() $\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
. The construction in the proof of the implication
$\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
. The construction in the proof of the implication
![]() $(1) \implies (2)$
of Theorem 4.4 then yields a closed subadditive function
$(1) \implies (2)$
of Theorem 4.4 then yields a closed subadditive function
![]() $c:[\kappa ]^2 \rightarrow \theta $
witnessing
$c:[\kappa ]^2 \rightarrow \theta $
witnessing
![]() $\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
such that, for all
$\operatorname {\mathrm {U}}(\kappa , 2, \theta , 2)$
such that, for all
![]() $(\alpha , \beta ) \in [\kappa ]^2$
, if
$(\alpha , \beta ) \in [\kappa ]^2$
, if
![]() $\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
, then
$\alpha \in \operatorname {\mathrm {acc}}(\kappa )$
, then
![]() $c(\alpha , \beta ) \geq i(\alpha ) = h(\alpha )$
. By Fact 3.2, c is moreover a witness to
$c(\alpha , \beta ) \geq i(\alpha ) = h(\alpha )$
. By Fact 3.2, c is moreover a witness to
![]() $\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \sup (\operatorname {\mathrm {Reg}}(\kappa )))$
.
$\operatorname {\mathrm {U}}(\kappa , \kappa , \theta , \sup (\operatorname {\mathrm {Reg}}(\kappa )))$
.
Our next result is Theorem B. It is very much in the spirit of [Reference Cox8, Corollary 3.10]; both results take instances of incompactness below a singular cardinal
![]() $\lambda $
and use them together with a scale of length
$\lambda $
and use them together with a scale of length
![]() $\lambda ^+$
to produce an instance of incompactness at
$\lambda ^+$
to produce an instance of incompactness at
![]() $\lambda ^+$
.
$\lambda ^+$
.
Theorem 5.4. Suppose that
![]() $\lambda $
is a singular cardinal,
$\lambda $
is a singular cardinal,
![]() $\theta \in \operatorname {\mathrm {Reg}}(\lambda ) \setminus (\operatorname {\mathrm {cf}}(\lambda ) + 1)$
, and
$\theta \in \operatorname {\mathrm {Reg}}(\lambda ) \setminus (\operatorname {\mathrm {cf}}(\lambda ) + 1)$
, and
![]() $\vec \lambda =\langle \lambda _j \mathrel {|} j < \operatorname {\mathrm {cf}}(\lambda ) \rangle $
is an increasing sequence of cardinals, converging to
$\vec \lambda =\langle \lambda _j \mathrel {|} j < \operatorname {\mathrm {cf}}(\lambda ) \rangle $
is an increasing sequence of cardinals, converging to
![]() $\lambda $
, such that:
$\lambda $
, such that:
-
•
 holds;
holds; -
•
 $\prod _{j < \operatorname {\mathrm {cf}}(\lambda )} \lambda _j^+$
carries a scale
$\prod _{j < \operatorname {\mathrm {cf}}(\lambda )} \lambda _j^+$
carries a scale
 $\vec {f}$
of length
$\vec {f}$
of length
 $\lambda ^+$
.
$\lambda ^+$
.
Then there is a
![]() $\Sigma $
-closed, subadditive witness to
$\Sigma $
-closed, subadditive witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
, where
$\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
, where
![]() $\Sigma \subseteq E^{\lambda ^+}_{\neq \operatorname {\mathrm {cf}}(\lambda )}$
denotes the set of good points for
$\Sigma \subseteq E^{\lambda ^+}_{\neq \operatorname {\mathrm {cf}}(\lambda )}$
denotes the set of good points for
![]() $\vec {f}$
.
$\vec {f}$
.
Proof Without loss of generality, assume that
![]() $\lambda _0>\theta $
. Fix sequences
$\lambda _0>\theta $
. Fix sequences
![]() $\langle X_{\alpha } \mathrel {|} \alpha < \lambda \rangle $
and
$\langle X_{\alpha } \mathrel {|} \alpha < \lambda \rangle $
and
![]() $\vec {C}^j = \langle C^j_{\alpha } \mathrel {|} \alpha < \lambda _j^+ \rangle $
for
$\vec {C}^j = \langle C^j_{\alpha } \mathrel {|} \alpha < \lambda _j^+ \rangle $
for
![]() $j < \operatorname {\mathrm {cf}}(\lambda )$
witnessing
$j < \operatorname {\mathrm {cf}}(\lambda )$
witnessing
![]() .
.
Let
![]() $j<\operatorname {\mathrm {cf}}(\lambda )$
be arbitrary. It is clear from the definition of
$j<\operatorname {\mathrm {cf}}(\lambda )$
be arbitrary. It is clear from the definition of
![]() that we may assume that
that we may assume that
![]() $\min (C^j_{\alpha }) \geq \lambda _j$
whenever
$\min (C^j_{\alpha }) \geq \lambda _j$
whenever
![]() $\alpha \in (\lambda _j, \lambda _j^+)$
. Now, define a function
$\alpha \in (\lambda _j, \lambda _j^+)$
. Now, define a function
![]() $h_j:\lambda _j^+ \rightarrow \theta $
by letting, for all
$h_j:\lambda _j^+ \rightarrow \theta $
by letting, for all
![]() $\alpha <\lambda _j^+$
,
$\alpha <\lambda _j^+$
,
 $$ \begin{align*}h_j(\alpha):=\begin{cases}X_{\alpha}, &\text{if }\alpha>\lambda_j\ \&\ X_{\alpha}\in\theta,\\ 0, &\text{otherwise}.\end{cases}\end{align*} $$
$$ \begin{align*}h_j(\alpha):=\begin{cases}X_{\alpha}, &\text{if }\alpha>\lambda_j\ \&\ X_{\alpha}\in\theta,\\ 0, &\text{otherwise}.\end{cases}\end{align*} $$
Claim 5.4.1. For all sufficiently large
![]() $j < \operatorname {\mathrm {cf}}(\lambda )$
,
$j < \operatorname {\mathrm {cf}}(\lambda )$
,
![]() $\vec {C}^j$
and
$\vec {C}^j$
and
![]() $h_j$
satisfy the hypotheses of Lemma 5.3.
$h_j$
satisfy the hypotheses of Lemma 5.3.
Proof We first show that
![]() $\vec {C}^j$
is a
$\vec {C}^j$
is a
![]() $\square (\lambda ^+_j)$
-sequence for all sufficiently large
$\square (\lambda ^+_j)$
-sequence for all sufficiently large
![]() $j < \operatorname {\mathrm {cf}}(\lambda )$
. Suppose for the sake of contradiction that there is an unbounded set
$j < \operatorname {\mathrm {cf}}(\lambda )$
. Suppose for the sake of contradiction that there is an unbounded set
![]() $J \subseteq \operatorname {\mathrm {cf}}(\lambda )$
such that, for all
$J \subseteq \operatorname {\mathrm {cf}}(\lambda )$
such that, for all
![]() $j \in J$
,
$j \in J$
,
![]() $\vec {C}^j$
is not a
$\vec {C}^j$
is not a
![]() $\square (\lambda _j^+)$
-sequence. Each
$\square (\lambda _j^+)$
-sequence. Each
![]() $\vec {C}^j$
is evidently a coherent C-sequence; therefore, for every
$\vec {C}^j$
is evidently a coherent C-sequence; therefore, for every
![]() $j \in J$
, we can fix a club
$j \in J$
, we can fix a club
![]() $D_j \subseteq \lambda _j^+$
such that
$D_j \subseteq \lambda _j^+$
such that
![]() $D_j \cap \alpha = C^j_{\alpha }$
for all
$D_j \cap \alpha = C^j_{\alpha }$
for all
![]() $\alpha \in \operatorname {\mathrm {acc}}(D_j)$
. By our assumption from the previous paragraph, this implies that
$\alpha \in \operatorname {\mathrm {acc}}(D_j)$
. By our assumption from the previous paragraph, this implies that
![]() $D_j \subseteq [\lambda _j, \lambda _j^+)$
. Fix a regular cardinal
$D_j \subseteq [\lambda _j, \lambda _j^+)$
. Fix a regular cardinal
![]() $\Upsilon $
sufficiently large to ensure that all objects of interest are in
$\Upsilon $
sufficiently large to ensure that all objects of interest are in
![]() $H_{\Upsilon }$
. Let
$H_{\Upsilon }$
. Let
![]() $p := \langle D_j \mathrel {|} j \in J \rangle $
,
$p := \langle D_j \mathrel {|} j \in J \rangle $
,
![]() $X^0 := 0$
and
$X^0 := 0$
and
![]() $X^1 := 1$
. Apply
$X^1 := 1$
. Apply
![]() twice to find
twice to find
![]() $N_0, N_1 \prec H_{\Upsilon }$
such that, for
$N_0, N_1 \prec H_{\Upsilon }$
such that, for
![]() $i < 2$
:
$i < 2$
:
-
•
 $p \in N_i$
;
$p \in N_i$
; -
•
 $|N_i| < \lambda $
;
$|N_i| < \lambda $
; -
•
 $N_i$
is internally approachable of length
$N_i$
is internally approachable of length
 $\operatorname {\mathrm {cf}}(\lambda )^+$
;
$\operatorname {\mathrm {cf}}(\lambda )^+$
; -
• for all sufficiently large
 $j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
$j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
 $X^i = X_{\sup (N_i \cap \lambda _j^+)}$
.
$X^i = X_{\sup (N_i \cap \lambda _j^+)}$
.
Now fix
![]() $j^* \in J$
sufficiently large so that, for
$j^* \in J$
sufficiently large so that, for
![]() $i < 2$
, we have
$i < 2$
, we have
-
•
 $|N_i| < \lambda _{j^*}$
;
$|N_i| < \lambda _{j^*}$
; -
•
 $X^i = X_{\sup (N_i \cap \lambda _{j^*}^+)}$
.
$X^i = X_{\sup (N_i \cap \lambda _{j^*}^+)}$
.
For each
![]() $i < 2$
, the ordinal
$i < 2$
, the ordinal
![]() $\beta _i := \sup (N_i \cap \lambda _j^+)$
is less than
$\beta _i := \sup (N_i \cap \lambda _j^+)$
is less than
![]() $\lambda _j^+$
. Since
$\lambda _j^+$
. Since
![]() $D_{j^*} \in N_i$
and
$D_{j^*} \in N_i$
and
![]() $D_{j^*}$
is club in
$D_{j^*}$
is club in
![]() $\lambda _j^+$
, we have
$\lambda _j^+$
, we have
![]() $\beta _i \in \operatorname {\mathrm {acc}}(D_{j^*})$
. In particular,
$\beta _i \in \operatorname {\mathrm {acc}}(D_{j^*})$
. In particular,
![]() $\beta _i>\lambda _{j^*}$
. By our choice of
$\beta _i>\lambda _{j^*}$
. By our choice of
![]() $D_{j^*}$
, it follows that
$D_{j^*}$
, it follows that
![]() $D_{j^*} \cap \beta _i = C^{j^*}_{\beta _i}$
. If
$D_{j^*} \cap \beta _i = C^{j^*}_{\beta _i}$
. If
![]() $\beta _0 < \beta _1$
, then
$\beta _0 < \beta _1$
, then
![]() $\beta _0 \in \operatorname {\mathrm {acc}}(D_{j^*})\cap \beta _1=\operatorname {\mathrm {acc}}(C^{j^*}_{\beta _1})$
and
$\beta _0 \in \operatorname {\mathrm {acc}}(D_{j^*})\cap \beta _1=\operatorname {\mathrm {acc}}(C^{j^*}_{\beta _1})$
and
![]() $\beta _1> \lambda _{j^*}$
, so
$\beta _1> \lambda _{j^*}$
, so
![]() $X_{\beta _0} = X_{\beta _1} \cap \beta _0$
. Likewise, if
$X_{\beta _0} = X_{\beta _1} \cap \beta _0$
. Likewise, if
![]() $\beta _1<\beta _0$
, then
$\beta _1<\beta _0$
, then
![]() $X_{\beta _1} = X_{\beta _0} \cap \beta _1$
. However, by our choice of
$X_{\beta _1} = X_{\beta _0} \cap \beta _1$
. However, by our choice of
![]() $j^*$
,
$j^*$
,
![]() $X_{\beta _0}=X^0=0$
and
$X_{\beta _0}=X^0=0$
and
![]() $X_{\beta _1}=X^1=1$
, which is a contradiction.
$X_{\beta _1}=X^1=1$
, which is a contradiction.
By the definition of
![]() $h_j$
and the fact that
$h_j$
and the fact that
![]() $\lambda _0>\theta $
, it is immediate that
$\lambda _0>\theta $
, it is immediate that
![]() $\vec {C}_j$
and
$\vec {C}_j$
and
![]() $h_j$
satisfy Clause (2) in the statement of Lemma 5.3. It remains to show that, for all sufficiently large
$h_j$
satisfy Clause (2) in the statement of Lemma 5.3. It remains to show that, for all sufficiently large
![]() $j < \operatorname {\mathrm {cf}}(\lambda )$
, for unboundedly many
$j < \operatorname {\mathrm {cf}}(\lambda )$
, for unboundedly many
![]() $i < \theta $
,
$i < \theta $
,
![]() $h_j^{-1}\{i\}$
is stationary in
$h_j^{-1}\{i\}$
is stationary in
![]() $\lambda _j^+$
. Suppose for the sake of contradiction that there is an unbounded
$\lambda _j^+$
. Suppose for the sake of contradiction that there is an unbounded
![]() $J \subseteq \operatorname {\mathrm {cf}}(\lambda )$
and, for each
$J \subseteq \operatorname {\mathrm {cf}}(\lambda )$
and, for each
![]() $j \in J$
, an
$j \in J$
, an
![]() $i_j < \theta $
such that
$i_j < \theta $
such that
![]() $h_j^{-1}\{i\}$
is nonstationary for all
$h_j^{-1}\{i\}$
is nonstationary for all
![]() $i \in [i_j, \theta )$
. Since
$i \in [i_j, \theta )$
. Since
![]() $\theta> \operatorname {\mathrm {cf}}(\lambda )$
is regular,
$\theta> \operatorname {\mathrm {cf}}(\lambda )$
is regular,
![]() $i^* := \sup \{i_j \mathrel {|} j < \operatorname {\mathrm {cf}}(\lambda )\}$
is less than
$i^* := \sup \{i_j \mathrel {|} j < \operatorname {\mathrm {cf}}(\lambda )\}$
is less than
![]() $\theta $
. It follows that for all
$\theta $
. It follows that for all
![]() $j \in J$
,
$j \in J$
,
![]() $h_j^{-1}[i^*, \theta )$
is nonstationary in
$h_j^{-1}[i^*, \theta )$
is nonstationary in
![]() $\lambda _j^+$
; fix a club
$\lambda _j^+$
; fix a club
![]() $D_j \subseteq \lambda _j^+$
disjoint from it. Fix a regular cardinal
$D_j \subseteq \lambda _j^+$
disjoint from it. Fix a regular cardinal
![]() $\Upsilon $
sufficiently large to ensure that all objects of interest are in
$\Upsilon $
sufficiently large to ensure that all objects of interest are in
![]() $H_{\Upsilon }$
. Let
$H_{\Upsilon }$
. Let
![]() $p := \{\theta , \vec {\lambda },\langle D_j \mathrel {|} j \in J \rangle \}$
and
$p := \{\theta , \vec {\lambda },\langle D_j \mathrel {|} j \in J \rangle \}$
and
![]() $X := i^*$
, and apply
$X := i^*$
, and apply
![]() to find
to find
![]() $N \prec H_{\Upsilon }$
such that:
$N \prec H_{\Upsilon }$
such that:
-
•
 $p \in N$
;
$p \in N$
; -
•
 $|N| < \lambda $
;
$|N| < \lambda $
; -
• N is internally approachable of length
 $\operatorname {\mathrm {cf}}(\lambda )^+$
;
$\operatorname {\mathrm {cf}}(\lambda )^+$
; -
• for all sufficiently large
 $j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
$j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
 $X = X_{\sup (N \cap \lambda _j^+)}$
.
$X = X_{\sup (N \cap \lambda _j^+)}$
.
Fix a sufficiently large
![]() $j^* \in J$
so that
$j^* \in J$
so that
![]() $|N| < \lambda _{j^*}$
and
$|N| < \lambda _{j^*}$
and
![]() $X = i^* = X_{\sup (N \cap \lambda _{j^*}^+)}$
. Let
$X = i^* = X_{\sup (N \cap \lambda _{j^*}^+)}$
. Let
![]() $\beta := \sup (N \cap \lambda _{j^*}^+)$
. Since
$\beta := \sup (N \cap \lambda _{j^*}^+)$
. Since
![]() $\vec {\lambda } \in N$
, we have
$\vec {\lambda } \in N$
, we have
![]() $\beta> \lambda _{j^*}$
, and hence
$\beta> \lambda _{j^*}$
, and hence
![]() $h_{j^*}(\beta ) = i^*$
. However, since
$h_{j^*}(\beta ) = i^*$
. However, since
![]() $D_{j^*}$
is a club in
$D_{j^*}$
is a club in
![]() $\lambda _{j^*}^+$
lying in N, we have
$\lambda _{j^*}^+$
lying in N, we have
![]() $\beta \in D_{j^*}$
, and hence
$\beta \in D_{j^*}$
, and hence
![]() $h_{j^*}(\beta ) < i^*$
. This is a contradiction, completing the proof of the claim.
$h_{j^*}(\beta ) < i^*$
. This is a contradiction, completing the proof of the claim.
By the claim, by discarding an initial segment of
![]() $\vec {\lambda }$
if necessary, we may assume that, for all
$\vec {\lambda }$
if necessary, we may assume that, for all
![]() $j < \operatorname {\mathrm {cf}}(\lambda )$
,
$j < \operatorname {\mathrm {cf}}(\lambda )$
,
![]() $\vec {C}^j$
and
$\vec {C}^j$
and
![]() $h_j$
satisfy the hypotheses of Lemma 5.3. We may therefore fix a closed, subadditive witness
$h_j$
satisfy the hypotheses of Lemma 5.3. We may therefore fix a closed, subadditive witness
![]() $c_j:[\lambda _j^+]^2 \rightarrow \theta $
to
$c_j:[\lambda _j^+]^2 \rightarrow \theta $
to
![]() $\operatorname {\mathrm {U}}(\lambda _j^+, \lambda _j^+, \theta , \lambda _j)$
such that
$\operatorname {\mathrm {U}}(\lambda _j^+, \lambda _j^+, \theta , \lambda _j)$
such that
![]() $c_j(\alpha , \beta ) \geq h_j(\alpha )$
for all
$c_j(\alpha , \beta ) \geq h_j(\alpha )$
for all
![]() $(\alpha , \beta ) \in [\lambda _j^+]^2$
with
$(\alpha , \beta ) \in [\lambda _j^+]^2$
with
![]() $\alpha \in \operatorname {\mathrm {acc}}(\lambda _j^+)$
.
$\alpha \in \operatorname {\mathrm {acc}}(\lambda _j^+)$
.
Next, let
![]() $\vec {f} = \langle f_{\beta } \mathrel {|} \beta < \lambda ^+ \rangle $
be a continuous scale in
$\vec {f} = \langle f_{\beta } \mathrel {|} \beta < \lambda ^+ \rangle $
be a continuous scale in
![]() $\prod _{j < \operatorname {\mathrm {cf}}(\lambda )} \lambda _j^+$
, and let
$\prod _{j < \operatorname {\mathrm {cf}}(\lambda )} \lambda _j^+$
, and let
![]() $\Sigma \subseteq E^{\lambda ^+}_{\neq \operatorname {\mathrm {cf}}(\lambda )}$
denote the set of good points for
$\Sigma \subseteq E^{\lambda ^+}_{\neq \operatorname {\mathrm {cf}}(\lambda )}$
denote the set of good points for
![]() $\vec {f}$
. Define a coloring
$\vec {f}$
. Define a coloring
![]() $c:[\lambda ^+]^2 \rightarrow \theta $
by setting, for all
$c:[\lambda ^+]^2 \rightarrow \theta $
by setting, for all
![]() $\beta <\gamma <\lambda ^+$
,
$\beta <\gamma <\lambda ^+$
,
Note that, for all
![]() $(\beta , \gamma ) \in [\lambda ^+]^2$
and all sufficiently large
$(\beta , \gamma ) \in [\lambda ^+]^2$
and all sufficiently large
![]() $j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
$j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
![]() $f_{\beta }(j) < f_{\gamma }(j)$
, so the above expression is well-defined. We claim that c is a
$f_{\beta }(j) < f_{\gamma }(j)$
, so the above expression is well-defined. We claim that c is a
![]() $\Sigma $
-closed, subadditive witness to
$\Sigma $
-closed, subadditive witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
. Let us verify each of these requirements in turn.
$\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
. Let us verify each of these requirements in turn.
Claim 5.4.2.
c is
![]() $\Sigma $
-closed.
$\Sigma $
-closed.
Proof Suppose that
![]() $\gamma < \lambda ^+$
,
$\gamma < \lambda ^+$
,
![]() $i < \theta $
, and
$i < \theta $
, and
![]() $B \subseteq D^c_{\leq i}(\gamma )$
, with
$B \subseteq D^c_{\leq i}(\gamma )$
, with
![]() $\beta := \sup (B)$
in
$\beta := \sup (B)$
in
![]() ${(\gamma \cap \Sigma ) \setminus B}$
. We will show that
${(\gamma \cap \Sigma ) \setminus B}$
. We will show that
![]() $\beta \in D^c_{\leq i}(\gamma )$
.
$\beta \in D^c_{\leq i}(\gamma )$
.
Since
![]() $\beta \in \Sigma $
, we can assume, by thinning out B if necessary, that there is
$\beta \in \Sigma $
, we can assume, by thinning out B if necessary, that there is
![]() $j_0 < \operatorname {\mathrm {cf}}(\lambda )$
such that, for all
$j_0 < \operatorname {\mathrm {cf}}(\lambda )$
such that, for all
![]() $(\alpha , \alpha ') \in [B]^2$
, we have
$(\alpha , \alpha ') \in [B]^2$
, we have
![]() $f_{\alpha } <_{j_0} f_{\alpha '}$
. Since
$f_{\alpha } <_{j_0} f_{\alpha '}$
. Since
![]() $\vec {f}$
is continuous, there is
$\vec {f}$
is continuous, there is
![]() $j_1 \in [j_0, \operatorname {\mathrm {cf}}(\lambda ))$
such that, for all
$j_1 \in [j_0, \operatorname {\mathrm {cf}}(\lambda ))$
such that, for all
![]() $j \in [j_1, \operatorname {\mathrm {cf}}(\lambda ))$
, we have
$j \in [j_1, \operatorname {\mathrm {cf}}(\lambda ))$
, we have
![]() $f_{\beta }(j) = \sup \{f_{\alpha }(j) \mathrel {|} \alpha \in B\}$
. Finally, since
$f_{\beta }(j) = \sup \{f_{\alpha }(j) \mathrel {|} \alpha \in B\}$
. Finally, since
![]() $B \subseteq D^c_{\leq i}(\gamma )$
, we can assume, by thinning out B again if necessary, that there is
$B \subseteq D^c_{\leq i}(\gamma )$
, we can assume, by thinning out B again if necessary, that there is
![]() $j_2$
with
$j_2$
with
![]() $j_1 \leq j_2 < \operatorname {\mathrm {cf}}(\lambda )$
such that, for all
$j_1 \leq j_2 < \operatorname {\mathrm {cf}}(\lambda )$
such that, for all
![]() $j \in [j_2, \operatorname {\mathrm {cf}}(\lambda ))$
,
$j \in [j_2, \operatorname {\mathrm {cf}}(\lambda ))$
,
-
•
 $f_{\beta }(j) < f_{\gamma }(j)$
;
$f_{\beta }(j) < f_{\gamma }(j)$
; -
• for all
 $\alpha \in B$
,
$\alpha \in B$
,
 $c_j(f_{\alpha }(j), f_{\gamma }(j)) \leq i$
.
$c_j(f_{\alpha }(j), f_{\gamma }(j)) \leq i$
.
Since each
![]() $c_j$
is closed, it follows that, for all
$c_j$
is closed, it follows that, for all
![]() $j \in [j_2,\operatorname {\mathrm {cf}}(\lambda ))$
, we have
$j \in [j_2,\operatorname {\mathrm {cf}}(\lambda ))$
, we have
![]() $\sup \{f_{\alpha }(j) \mathrel {|} \alpha \in B\} = f_{\beta }(j)$
and
$\sup \{f_{\alpha }(j) \mathrel {|} \alpha \in B\} = f_{\beta }(j)$
and
![]() $c_j(f_{\beta }(j), f_{\gamma }(j)) \leq i$
, and hence
$c_j(f_{\beta }(j), f_{\gamma }(j)) \leq i$
, and hence
![]() $c(\beta , \gamma ) \leq i$
.
$c(\beta , \gamma ) \leq i$
.
Claim 5.4.3. c is subadditive.
Proof Let
![]() $\alpha < \beta < \gamma < \lambda ^+$
be arbitrary. For all sufficiently large
$\alpha < \beta < \gamma < \lambda ^+$
be arbitrary. For all sufficiently large
![]() $j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
$j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
![]() $f_{\alpha }(j) < f_{\beta }(j) < f_{\gamma }(j)$
and hence, since each
$f_{\alpha }(j) < f_{\beta }(j) < f_{\gamma }(j)$
and hence, since each
![]() $c_j$
is subadditive, we have
$c_j$
is subadditive, we have
-
•
 $c_j(f_{\alpha }(j), f_{\gamma }(j)) \leq \max \{c_j(f_{\alpha }(j), f_{\beta }(j)), c_j(f_{\beta }(j), f_{\gamma }(j))\}$
; and
$c_j(f_{\alpha }(j), f_{\gamma }(j)) \leq \max \{c_j(f_{\alpha }(j), f_{\beta }(j)), c_j(f_{\beta }(j), f_{\gamma }(j))\}$
; and -
•
 $c_j(f_{\alpha }(j), f_{\beta }(j)) \leq \max \{c_j(f_{\alpha }(j), f_{\gamma }(j)), c_j(f_{\beta }(j), f_{\gamma }(j))\}$
.
$c_j(f_{\alpha }(j), f_{\beta }(j)) \leq \max \{c_j(f_{\alpha }(j), f_{\gamma }(j)), c_j(f_{\beta }(j), f_{\gamma }(j))\}$
.
It follows immediately from the definition of c that
![]() $c(\alpha , \gamma ) \leq \max \{c(\alpha , \beta ), c(\beta , \gamma )\}$
and
$c(\alpha , \gamma ) \leq \max \{c(\alpha , \beta ), c(\beta , \gamma )\}$
and
![]() $c(\alpha , \beta ) \leq \max \{c(\alpha , \gamma ), c(\beta , \gamma )\}$
.
$c(\alpha , \beta ) \leq \max \{c(\alpha , \gamma ), c(\beta , \gamma )\}$
.
Claim 5.4.4.
c witnesses
![]() $\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
.
$\operatorname {\mathrm {U}}(\lambda ^+, \lambda ^+, \theta , \lambda )$
.
Proof By a theorem of Shelah,
![]() $\Sigma \cap E^{\lambda ^+}_{\ge \chi }$
is stationary for all
$\Sigma \cap E^{\lambda ^+}_{\ge \chi }$
is stationary for all
![]() $\chi <\lambda $
. So, since c is
$\chi <\lambda $
. So, since c is
![]() $\Sigma $
-closed and subadditive, Lemma 3.2(3) implies that it suffices to verify that c witnesses
$\Sigma $
-closed and subadditive, Lemma 3.2(3) implies that it suffices to verify that c witnesses
![]() $\operatorname {\mathrm {U}}(\lambda ^+, 2, \theta , 2)$
. To this end, fix
$\operatorname {\mathrm {U}}(\lambda ^+, 2, \theta , 2)$
. To this end, fix
![]() $A \in [\lambda ^+]^{\lambda ^+}$
and a color
$A \in [\lambda ^+]^{\lambda ^+}$
and a color
![]() $i < \theta $
. We will find
$i < \theta $
. We will find
![]() $(\alpha , \gamma ) \in [A]^2$
such that
$(\alpha , \gamma ) \in [A]^2$
such that
![]() $c(\alpha , \gamma )> i$
.
$c(\alpha , \gamma )> i$
.
Fix a regular cardinal
![]() $\Upsilon $
sufficiently large to ensure that all objects of interest are in
$\Upsilon $
sufficiently large to ensure that all objects of interest are in
![]() $H_{\Upsilon }$
. Apply
$H_{\Upsilon }$
. Apply
![]() with
with
![]() $p:=\{\vec \lambda ,\vec f,A\}$
and
$p:=\{\vec \lambda ,\vec f,A\}$
and
![]() $X := i+1$
to find
$X := i+1$
to find
![]() $N \prec H_{\Upsilon }$
such that:
$N \prec H_{\Upsilon }$
such that:
-
•
 $p\in N$
;
$p\in N$
; -
•
 $|N| < \lambda $
;
$|N| < \lambda $
; -
• N is internally approachable of length
 $\operatorname {\mathrm {cf}}(\lambda )^+$
;
$\operatorname {\mathrm {cf}}(\lambda )^+$
; -
• for all sufficiently large
 $j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
$j < \operatorname {\mathrm {cf}}(\lambda )$
, we have
 $X_{\sup (N \cap \lambda _j^+)} = i+1$
.
$X_{\sup (N \cap \lambda _j^+)} = i+1$
.
As
![]() $|N|<\lambda $
and
$|N|<\lambda $
and
![]() $\vec \lambda \in N$
, there exists a function
$\vec \lambda \in N$
, there exists a function
![]() $\chi _N\in \prod _{j<\operatorname {\mathrm {cf}}(\lambda )}\operatorname {\mathrm {acc}}(\lambda _j^+)$
such that
$\chi _N\in \prod _{j<\operatorname {\mathrm {cf}}(\lambda )}\operatorname {\mathrm {acc}}(\lambda _j^+)$
such that
![]() $\chi _N(j)=\sup (N\cap \lambda _j^+)$
for all sufficiently large
$\chi _N(j)=\sup (N\cap \lambda _j^+)$
for all sufficiently large
![]() $j<\operatorname {\mathrm {cf}}(\lambda )$
. Let
$j<\operatorname {\mathrm {cf}}(\lambda )$
. Let
![]() $\beta :=\sup (N\cap \lambda ^+)$
. As N is internally approachable of length
$\beta :=\sup (N\cap \lambda ^+)$
. As N is internally approachable of length
![]() $\operatorname {\mathrm {cf}}(\lambda )^+$
, we know that
$\operatorname {\mathrm {cf}}(\lambda )^+$
, we know that
![]() $\beta \in \Sigma \cap E^{\lambda ^+}_{\operatorname {\mathrm {cf}}(\lambda )^+}$
. Since
$\beta \in \Sigma \cap E^{\lambda ^+}_{\operatorname {\mathrm {cf}}(\lambda )^+}$
. Since
![]() $\vec {f} \in N$
,
$\vec {f} \in N$
,
![]() $\vec {f}$
is continuous, and N is internally approachable, we know that
$\vec {f}$
is continuous, and N is internally approachable, we know that
![]() $f_{\beta }(j) = \chi _N(j)$
for all sufficiently large
$f_{\beta }(j) = \chi _N(j)$
for all sufficiently large
![]() $j<\operatorname {\mathrm {cf}}(\lambda )$
. Thus, for all sufficiently large
$j<\operatorname {\mathrm {cf}}(\lambda )$
. Thus, for all sufficiently large
![]() $j<\operatorname {\mathrm {cf}}(\lambda )$
and all
$j<\operatorname {\mathrm {cf}}(\lambda )$
and all
![]() $\eta \in (f_{\beta }(j), \lambda _j^+)$
,
$\eta \in (f_{\beta }(j), \lambda _j^+)$
,
Consequently,
![]() $c(\beta , \gamma )>i$
for all
$c(\beta , \gamma )>i$
for all
![]() $\gamma>\beta $
.
$\gamma>\beta $
.
Fix
![]() $\gamma \in A \setminus (\beta + 1)$
. Since
$\gamma \in A \setminus (\beta + 1)$
. Since
![]() $\beta \in \Sigma $
and c is
$\beta \in \Sigma $
and c is
![]() $\Sigma $
-closed, there is
$\Sigma $
-closed, there is
![]() $\epsilon < \beta $
such that
$\epsilon < \beta $
such that
![]() $c(\alpha , \gamma )>i$
for all
$c(\alpha , \gamma )>i$
for all
![]() $\alpha \in (\epsilon , \beta )$
. As
$\alpha \in (\epsilon , \beta )$
. As
![]() $A\in N$
, the elementarity of N entails that
$A\in N$
, the elementarity of N entails that
![]() $\sup (A \cap \beta ) = \beta $
, so we may fix
$\sup (A \cap \beta ) = \beta $
, so we may fix
![]() $\alpha \in A \cap (\epsilon , \beta )$
. Then
$\alpha \in A \cap (\epsilon , \beta )$
. Then
![]() $c(\alpha , \gamma )>i$
, as desired.
$c(\alpha , \gamma )>i$
, as desired.
We now connect the above finding with the notion of the C-sequence spectrum, introduced in Part II of this series.
Definition 5.5 [Reference Lambie-Hanson and Rinot22].
-
(1) For every C-sequence
 $\vec {C} = \langle C_{\beta } \mathrel {|} \beta < \kappa \rangle $
,
$\vec {C} = \langle C_{\beta } \mathrel {|} \beta < \kappa \rangle $
,
 $\chi (\vec {C})$
is the least cardinal
$\chi (\vec {C})$
is the least cardinal
 $\chi \leq \kappa $
such that there exist
$\chi \leq \kappa $
such that there exist
 $\Delta \in [\kappa ]^{\kappa }$
and
$\Delta \in [\kappa ]^{\kappa }$
and
 $b:\kappa \rightarrow [\kappa ]^{\chi }$
with
$b:\kappa \rightarrow [\kappa ]^{\chi }$
with
 $\Delta \cap \alpha \subseteq \bigcup _{\beta \in b(\alpha )}C_{\beta }$
for every
$\Delta \cap \alpha \subseteq \bigcup _{\beta \in b(\alpha )}C_{\beta }$
for every
 $\alpha <\kappa $
.
$\alpha <\kappa $
. -
(2)
 $\operatorname {\mathrm {Cspec}}(\kappa ) := \{\chi (\vec {C}) \mathrel {|} \vec {C}$
is a C-sequence over
$\operatorname {\mathrm {Cspec}}(\kappa ) := \{\chi (\vec {C}) \mathrel {|} \vec {C}$
is a C-sequence over
 $\kappa \} \setminus \omega $
.
$\kappa \} \setminus \omega $
.
The next result yields the “In particular” part of Theorem B.
Corollary 5.6. Suppose that
![]() $\lambda $
is a singular cardinal,
$\lambda $
is a singular cardinal,
![]() $\vec \lambda $
is an increasing
$\vec \lambda $
is an increasing
![]() $\operatorname {\mathrm {cf}}(\lambda )$
-sequence of cardinals, converging to
$\operatorname {\mathrm {cf}}(\lambda )$
-sequence of cardinals, converging to
![]() $\lambda $
, such that
$\lambda $
, such that
![]() holds, and
holds, and
![]() $\operatorname {\mathrm {tcf}}(\prod \vec \lambda ,<^*)=\lambda ^+$
. Then
$\operatorname {\mathrm {tcf}}(\prod \vec \lambda ,<^*)=\lambda ^+$
. Then
![]() $\operatorname {\mathrm {Reg}}(\lambda )\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
$\operatorname {\mathrm {Reg}}(\lambda )\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
Proof
-
▸ By Remark 5.2,
 $2^{\operatorname {\mathrm {cf}}(\lambda )}<\lambda $
. So, by [Reference Lambie-Hanson and Rinot22, Theorem 5.29(1)],
$2^{\operatorname {\mathrm {cf}}(\lambda )}<\lambda $
. So, by [Reference Lambie-Hanson and Rinot22, Theorem 5.29(1)],
 $\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
$\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
. -
▸ By [Reference Lambie-Hanson and Rinot22, Lemma 4.11],
 $\operatorname {\mathrm {cf}}(\lambda )\in \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
$\operatorname {\mathrm {cf}}(\lambda )\in \operatorname {\mathrm {Cspec}}(\lambda ^+)$
. -
▸ By Theorem 5.4 and [Reference Lambie-Hanson and Rinot22, Corollary 5.21],
 $\operatorname {\mathrm {Reg}}(\lambda )\setminus (\operatorname {\mathrm {cf}}(\lambda )+1)\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
$\operatorname {\mathrm {Reg}}(\lambda )\setminus (\operatorname {\mathrm {cf}}(\lambda )+1)\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
Our next goal is to improve the following fact from Part II, and present a weaker sufficient condition for
![]() $\operatorname {\mathrm {Cspec}}(\lambda ^+)$
to cover
$\operatorname {\mathrm {Cspec}}(\lambda ^+)$
to cover
![]() $\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))$
.
$\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))$
.
Fact 5.7 [Reference Lambie-Hanson and Rinot22, Theorem 5.29(2)].
Suppose that
![]() $\lambda $
is a singular cardinal of successor cofinality
$\lambda $
is a singular cardinal of successor cofinality
![]() $\mu ^+$
. Then:
$\mu ^+$
. Then:
-
•
 $\operatorname {\mathrm {Reg}}(\mu )\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
$\operatorname {\mathrm {Reg}}(\mu )\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
. -
• If
 $2^{\mu }\le \lambda $
, then
$2^{\mu }\le \lambda $
, then
 $\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
$\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
Theorem 5.8. Suppose that
![]() $\lambda $
is a singular cardinal. If
$\lambda $
is a singular cardinal. If
![]() $\lambda $
is of uncountable cofinality, suppose also that
$\lambda $
is of uncountable cofinality, suppose also that
![]() $\chi (\operatorname {\mathrm {cf}}(\lambda ))>1$
. Then, for every infinite regular
$\chi (\operatorname {\mathrm {cf}}(\lambda ))>1$
. Then, for every infinite regular
![]() $\theta \le \operatorname {\mathrm {cf}}(\lambda )$
, there exists a closed witness to
$\theta \le \operatorname {\mathrm {cf}}(\lambda )$
, there exists a closed witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\theta ,\operatorname {\mathrm {cf}}(\lambda ))$
.
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\theta ,\operatorname {\mathrm {cf}}(\lambda ))$
.
Proof By [Reference Lambie-Hanson and Rinot20, Corollary 4.17], there exists a closed witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ), \operatorname {\mathrm {cf}}(\lambda ))$
, so assume that
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\operatorname {\mathrm {cf}}(\lambda ), \operatorname {\mathrm {cf}}(\lambda ))$
, so assume that
![]() $\lambda $
has uncountable cofinality. Denote
$\lambda $
has uncountable cofinality. Denote
![]() $\nu :=\operatorname {\mathrm {cf}}(\lambda )$
, so that
$\nu :=\operatorname {\mathrm {cf}}(\lambda )$
, so that
![]() $\chi (\nu )>1$
. Recalling Claim 4.21.3 from the proof of [Reference Lambie-Hanson and Rinot20, Theorem 4.21], it suffices to prove that the ideal
$\chi (\nu )>1$
. Recalling Claim 4.21.3 from the proof of [Reference Lambie-Hanson and Rinot20, Theorem 4.21], it suffices to prove that the ideal
![]() $\mathcal I$
defined there in “Case 1: Uncountable cofinality” is not weakly
$\mathcal I$
defined there in “Case 1: Uncountable cofinality” is not weakly
![]() $\nu $
-saturated.
$\nu $
-saturated.
Let us first remind the reader that the definition of the ideal
![]() $\mathcal I$
goes through first fixing a stationary subset
$\mathcal I$
goes through first fixing a stationary subset
![]() $\Delta \subseteq E^{\lambda ^+}_{\operatorname {\mathrm {cf}}(\lambda )}$
and a sequence
$\Delta \subseteq E^{\lambda ^+}_{\operatorname {\mathrm {cf}}(\lambda )}$
and a sequence
![]() $\vec e=\langle e_{\delta }\mathrel {|} \delta \in \Delta \rangle $
such that:
$\vec e=\langle e_{\delta }\mathrel {|} \delta \in \Delta \rangle $
such that:
-
• for every
 $\delta \in \Delta $
,
$\delta \in \Delta $
,
 $e_{\delta }$
is a club in
$e_{\delta }$
is a club in
 $\delta $
of order type
$\delta $
of order type
 $\operatorname {\mathrm {cf}}(\lambda )$
;
$\operatorname {\mathrm {cf}}(\lambda )$
; -
• for every
 $\delta \in \Delta $
,
$\delta \in \Delta $
,
 $\langle \operatorname {\mathrm {cf}}(\gamma )\mathrel {|} \gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })\rangle $
is strictly increasing and converging to
$\langle \operatorname {\mathrm {cf}}(\gamma )\mathrel {|} \gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })\rangle $
is strictly increasing and converging to
 $\lambda $
;
$\lambda $
; -
• for every club D in
 $\lambda ^+$
, there exists
$\lambda ^+$
, there exists
 $\delta \in \Delta $
such that
$\delta \in \Delta $
such that
 $e_{\delta }\subseteq D$
.
$e_{\delta }\subseteq D$
.
Then, the ideal
![]() $\mathcal I$
consists of all subsets
$\mathcal I$
consists of all subsets
![]() $\Gamma \subseteq \lambda ^+$
for which there exists a club
$\Gamma \subseteq \lambda ^+$
for which there exists a club
![]() $D\subseteq \lambda ^+$
such that
$D\subseteq \lambda ^+$
such that
![]() $\sup (\operatorname {\mathrm {nacc}}(e_{\delta })\cap D\cap \Gamma )<\delta $
for every
$\sup (\operatorname {\mathrm {nacc}}(e_{\delta })\cap D\cap \Gamma )<\delta $
for every
![]() $\delta \in \Delta \cap D$
.
$\delta \in \Delta \cap D$
.
Now, since
![]() $\chi (\nu )>1$
, by [Reference Inamdar and Rinot12, Theorem A],
$\chi (\nu )>1$
, by [Reference Inamdar and Rinot12, Theorem A],
![]() $\operatorname {\mathrm {\textsf {unbounded}}}^+(J^{\textrm {bd}}[\nu ],\nu )$
holds. That is, we may fix a coloring
$\operatorname {\mathrm {\textsf {unbounded}}}^+(J^{\textrm {bd}}[\nu ],\nu )$
holds. That is, we may fix a coloring
![]() $c:[\nu ]^2\rightarrow \nu $
satisfying that, for every cofinal
$c:[\nu ]^2\rightarrow \nu $
satisfying that, for every cofinal
![]() $B\subseteq \nu $
, there exist
$B\subseteq \nu $
, there exist
![]() $(\eta ,T)\in (\nu ,[\nu ]^{\nu })$
such that, for all
$(\eta ,T)\in (\nu ,[\nu ]^{\nu })$
such that, for all
![]() $\tau \in T$
,
$\tau \in T$
,
![]() $\sup \{\beta \in B\mathrel {|} c(\eta ,\beta )=\tau \}=\nu $
.
$\sup \{\beta \in B\mathrel {|} c(\eta ,\beta )=\tau \}=\nu $
.
Fix a club
![]() $\Lambda $
in
$\Lambda $
in
![]() $\lambda $
of order-type
$\lambda $
of order-type
![]() $\nu $
. For every
$\nu $
. For every
![]() $\eta <\nu $
and
$\eta <\nu $
and
![]() $\tau <\nu $
, let
$\tau <\nu $
, let
Claim 5.8.1. There exists
![]() $\eta <\nu $
such that
$\eta <\nu $
such that
![]() $|\{ \tau <\nu \mathrel {|} \Gamma ^{\tau }_{\eta }\in \mathcal I^+\}|=\nu $
.
$|\{ \tau <\nu \mathrel {|} \Gamma ^{\tau }_{\eta }\in \mathcal I^+\}|=\nu $
.
Proof Suppose not. Then, for every
![]() $\eta <\nu $
, the set
$\eta <\nu $
, the set
![]() $T_{\eta }:=\{ \tau <\nu \mathrel {|} \Gamma ^{\tau }_{\eta }\in \mathcal I^+\}$
is bounded in
$T_{\eta }:=\{ \tau <\nu \mathrel {|} \Gamma ^{\tau }_{\eta }\in \mathcal I^+\}$
is bounded in
![]() $\nu $
. For each
$\nu $
. For each
![]() $\eta <\nu $
and
$\eta <\nu $
and
![]() $\tau \in \nu \setminus T_{\eta }$
, fix a club
$\tau \in \nu \setminus T_{\eta }$
, fix a club
![]() $D_{\eta }^{\tau }\subseteq \lambda ^+$
such that
$D_{\eta }^{\tau }\subseteq \lambda ^+$
such that
![]() $\sup (\operatorname {\mathrm {nacc}}(e_{\delta })\cap D_{\eta }^{\tau }\cap \Gamma _{\eta }^{\tau })<\delta $
for every
$\sup (\operatorname {\mathrm {nacc}}(e_{\delta })\cap D_{\eta }^{\tau }\cap \Gamma _{\eta }^{\tau })<\delta $
for every
![]() $\delta \in \Delta \cap D^{\eta }_{\tau }$
. Let
$\delta \in \Delta \cap D^{\eta }_{\tau }$
. Let
![]() $D:=\bigcap \{ D_{\eta }^{\tau }\mathrel {|} \eta <\nu , \tau \in \nu \setminus T_{\eta }\}$
. Now, using the choice of
$D:=\bigcap \{ D_{\eta }^{\tau }\mathrel {|} \eta <\nu , \tau \in \nu \setminus T_{\eta }\}$
. Now, using the choice of
![]() $\vec e$
, let us fix
$\vec e$
, let us fix
![]() $\delta \in \Delta $
such that
$\delta \in \Delta $
such that
![]() $e_{\delta }\subseteq D$
. In particular,
$e_{\delta }\subseteq D$
. In particular,
![]() ${\delta \in D}$
. As
${\delta \in D}$
. As
![]() $\langle \operatorname {\mathrm {cf}}(\gamma )\mathrel {|} \gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })\rangle $
is strictly increasing and converging to
$\langle \operatorname {\mathrm {cf}}(\gamma )\mathrel {|} \gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })\rangle $
is strictly increasing and converging to
![]() $\lambda $
, it follows that
$\lambda $
, it follows that
![]() $B:=\{ \operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))\mathrel {|} \gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })\}$
is cofinal in
$B:=\{ \operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))\mathrel {|} \gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })\}$
is cofinal in
![]() $\nu $
. Thus, by the choice of c, we may now find
$\nu $
. Thus, by the choice of c, we may now find
![]() $(\eta ,T)\in (\nu ,[\nu ]^{\nu })$
such that, for all
$(\eta ,T)\in (\nu ,[\nu ]^{\nu })$
such that, for all
![]() $\tau \in T$
,
$\tau \in T$
,
![]() $\sup \{\beta \in B\mathrel {|} c(\eta ,\beta )=\tau \}=\nu $
. Pick
$\sup \{\beta \in B\mathrel {|} c(\eta ,\beta )=\tau \}=\nu $
. Pick
![]() $\tau \in T\setminus T_{\eta }$
. As
$\tau \in T\setminus T_{\eta }$
. As
![]() $\delta \in \Delta \cap D\subseteq \Delta \cap D_{\eta }^{\tau }$
, we infer that
$\delta \in \Delta \cap D\subseteq \Delta \cap D_{\eta }^{\tau }$
, we infer that
![]() ${\sup (\operatorname {\mathrm {nacc}}(e_{\delta })\cap D_{\eta }^{\tau }\cap \Gamma _{\eta }^{\tau })<\delta }$
. In particular,
${\sup (\operatorname {\mathrm {nacc}}(e_{\delta })\cap D_{\eta }^{\tau }\cap \Gamma _{\eta }^{\tau })<\delta }$
. In particular,
![]() $A:=\{\operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))\mathrel {|} \gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })\cap D_{\eta }^{\tau }\cap \Gamma _{\eta }^{\tau }\}$
is bounded in
$A:=\{\operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))\mathrel {|} \gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })\cap D_{\eta }^{\tau }\cap \Gamma _{\eta }^{\tau }\}$
is bounded in
![]() $\nu $
. Pick
$\nu $
. Pick
![]() $\beta \in B$
above
$\beta \in B$
above
![]() $\sup (A\cup (\eta +1))$
such that
$\sup (A\cup (\eta +1))$
such that
![]() $c(\eta ,\beta )=\tau $
. Then, find
$c(\eta ,\beta )=\tau $
. Then, find
![]() $\gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })$
such that
$\gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })$
such that
![]() $\beta =\operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))$
. Altogether:
$\beta =\operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))$
. Altogether:
-
•
 $\gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })$
;
$\gamma \in \operatorname {\mathrm {nacc}}(e_{\delta })$
; -
•
 $\gamma \in e_{\delta }$
, so that
$\gamma \in e_{\delta }$
, so that
 $\gamma \in D\subseteq D^{\tau }_{\eta }$
;
$\gamma \in D\subseteq D^{\tau }_{\eta }$
; -
•
 $c(\eta ,\operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))=c(\eta ,\beta )=\tau $
, so that
$c(\eta ,\operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))=c(\eta ,\beta )=\tau $
, so that
 $\gamma \in \Gamma ^{\tau }_{\eta }$
;
$\gamma \in \Gamma ^{\tau }_{\eta }$
; -
•
 $\operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))=\beta>\sup (A)$
, so that
$\operatorname {\mathrm {otp}}(\Lambda \cap \operatorname {\mathrm {cf}}(\gamma ))=\beta>\sup (A)$
, so that
 $\gamma \notin \operatorname {\mathrm {nacc}}(e_{\delta })\cap D_{\eta }^{\tau }\cap \Gamma _{\eta }^{\tau }$
.
$\gamma \notin \operatorname {\mathrm {nacc}}(e_{\delta })\cap D_{\eta }^{\tau }\cap \Gamma _{\eta }^{\tau }$
.
This is a contradiction.
It follows that
![]() $\mathcal I$
is indeed not weakly
$\mathcal I$
is indeed not weakly
![]() $\nu $
-saturated, so we are done.
$\nu $
-saturated, so we are done.
As successor cardinals are non-Mahlo, the following indeed improves Fact 5.7.
Corollary 5.9. Suppose that
![]() $\lambda $
is a singular cardinal of cofinality
$\lambda $
is a singular cardinal of cofinality
![]() $\nu $
. If
$\nu $
. If
![]() $\nu $
is not greatly Mahlo, then
$\nu $
is not greatly Mahlo, then
![]() $\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
$\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))\subseteq \operatorname {\mathrm {Cspec}}(\lambda ^+)$
.
Proof By [Reference Lambie-Hanson and Rinot22, Corollary 5.21], to show that an infinite regular cardinal
![]() $\theta $
is in
$\theta $
is in
![]() $\operatorname {\mathrm {Cspec}}(\lambda ^+)$
, it suffices to prove that there exists a closed witness to
$\operatorname {\mathrm {Cspec}}(\lambda ^+)$
, it suffices to prove that there exists a closed witness to
![]() $\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\theta ,\theta )$
. By the preceding theorem, if
$\operatorname {\mathrm {U}}(\lambda ^+,\lambda ^+,\theta ,\theta )$
. By the preceding theorem, if
![]() $\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))$
is not a subset of
$\operatorname {\mathrm {Reg}}(\operatorname {\mathrm {cf}}(\lambda ))$
is not a subset of
![]() $\operatorname {\mathrm {Cspec}}(\lambda ^+)$
, then
$\operatorname {\mathrm {Cspec}}(\lambda ^+)$
, then
![]() $\operatorname {\mathrm {cf}}(\lambda )$
is an uncountable cardinal and
$\operatorname {\mathrm {cf}}(\lambda )$
is an uncountable cardinal and
![]() $\chi (\operatorname {\mathrm {cf}}(\lambda ))\le 1$
. In this case, by [Reference Lambie-Hanson and Rinot22, Theorem A(2)],
$\chi (\operatorname {\mathrm {cf}}(\lambda ))\le 1$
. In this case, by [Reference Lambie-Hanson and Rinot22, Theorem A(2)],
![]() $\operatorname {\mathrm {cf}}(\lambda )$
is greatly Mahlo.
$\operatorname {\mathrm {cf}}(\lambda )$
is greatly Mahlo.
6 Stationarily layered posets
In Part I of this project [Reference Lambie-Hanson and Rinot20], we motivated the study of
![]() $\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
by showing that it places limits on the infinite productivity of the
$\operatorname {\mathrm {U}}(\kappa , \mu , \theta , \chi )$
by showing that it places limits on the infinite productivity of the
![]() $\kappa $
-Knaster condition. Here, we present an analogous result, indicating that closed witnesses to
$\kappa $
-Knaster condition. Here, we present an analogous result, indicating that closed witnesses to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2, \theta , 2)$
place limits on the infinite productivity of the property of being
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2, \theta , 2)$
place limits on the infinite productivity of the property of being
![]() $\kappa $
-stationarily layered, which is a strengthening of the
$\kappa $
-stationarily layered, which is a strengthening of the
![]() $\kappa $
-Knaster condition.
$\kappa $
-Knaster condition.
Definition 6.1 [Reference Cummings, Foreman and Magidor6].
A partial order
![]() $\mathbb {P}$
is
$\mathbb {P}$
is
![]() $\kappa $
-stationarily layered if the collection of regular suborders of
$\kappa $
-stationarily layered if the collection of regular suborders of
![]() $\mathbb {P}$
of size less than
$\mathbb {P}$
of size less than
![]() $\kappa $
is stationary in
$\kappa $
is stationary in
![]() $\mathcal {P}_{\kappa }(\mathbb {P})$
.
$\mathcal {P}_{\kappa }(\mathbb {P})$
.
By [Reference Cox7, Lemma 1.5], any
![]() $\kappa $
-stationarily layered poset is also
$\kappa $
-stationarily layered poset is also
![]() $\kappa $
-Knaster. We now recall a useful equivalence.
$\kappa $
-Knaster. We now recall a useful equivalence.
Fact 6.2 [Reference Cox7, Lemma 2.3].
Given a poset
![]() $\mathbb {P}$
, the following are equivalent.
$\mathbb {P}$
, the following are equivalent.
-
(1)
 $\mathbb {P}$
is
$\mathbb {P}$
is
 $\kappa $
-stationarily layered.
$\kappa $
-stationarily layered. -
(2) There is a regular cardinal
 $\Upsilon $
with
$\Upsilon $
with
 $\mathcal {P}_{\kappa }(\mathbb {P}) \in H_{\Upsilon }$
and an elementary substructure
$\mathcal {P}_{\kappa }(\mathbb {P}) \in H_{\Upsilon }$
and an elementary substructure
 $M \prec H_{\Upsilon }$
such that:
$M \prec H_{\Upsilon }$
such that:-
(a)
 $\kappa ,\mathbb {P}\in M$
;
$\kappa ,\mathbb {P}\in M$
; -
(b)
 $\kappa \cap M \in \kappa $
;
$\kappa \cap M \in \kappa $
; -
(c)
 $\mathbb {P} \cap M$
is a regular suborder of
$\mathbb {P} \cap M$
is a regular suborder of
 $\mathbb {P}$
.
$\mathbb {P}$
.
-
The following is Theorem D:
Theorem 6.3. Suppose that
![]() $\theta \leq \chi < \kappa $
are infinite, regular cardinals,
$\theta \leq \chi < \kappa $
are infinite, regular cardinals,
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\chi $
-inaccessible, and
${<}\chi $
-inaccessible, and
![]() $c:[\kappa ]^2\rightarrow \theta $
is a closed witness to
$c:[\kappa ]^2\rightarrow \theta $
is a closed witness to
![]() $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
that is subadditive of the second kind. Then:
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
that is subadditive of the second kind. Then:
-
• There is a sequence of posets
 $\langle \mathbb {P}_i \mathrel {|} i < \theta \rangle $
such that:
$\langle \mathbb {P}_i \mathrel {|} i < \theta \rangle $
such that:-
(1) for all
 $i < \theta $
,
$i < \theta $
,
 $\mathbb {P}_i$
is well-met and
$\mathbb {P}_i$
is well-met and
 $\chi $
-directed closed with greatest lower bounds
$\chi $
-directed closed with greatest lower bounds
 $;$
$;$
-
(2) for all
 $j < \theta $
,
$j < \theta $
,
 $\prod _{i < j} \mathbb {P}_i$
is
$\prod _{i < j} \mathbb {P}_i$
is
 $\kappa $
-stationarily layered
$\kappa $
-stationarily layered
 $;$
$;$
-
(3)
 $\prod _{i < \theta } \mathbb {P}_i$
is not
$\prod _{i < \theta } \mathbb {P}_i$
is not
 $\kappa $
-cc.
$\kappa $
-cc.
-
-
• There is a poset
 $\mathbb P$
such that, if
$\mathbb P$
such that, if
 $\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then:
$\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then:-
(1)
 $\mathbb {P}$
is well-met and
$\mathbb {P}$
is well-met and
 $\chi $
-directed closed with greatest lower bounds
$\chi $
-directed closed with greatest lower bounds
 $;$
$;$
-
(2) for all
 $j < \theta $
,
$j < \theta $
,
 $\mathbb {P}^j$
is
$\mathbb {P}^j$
is
 $\kappa $
-stationarily layered
$\kappa $
-stationarily layered
 $;$
$;$
-
(3)
 $\mathbb {P}^{\theta }$
is not
$\mathbb {P}^{\theta }$
is not
 $\kappa $
-cc.
$\kappa $
-cc.
-
Proof Using Lemma 2.4(3) (with
![]() $S:=E^{\kappa }_{\chi }$
), let us fix
$S:=E^{\kappa }_{\chi }$
), let us fix
![]() $\epsilon <\kappa $
such that, for every
$\epsilon <\kappa $
such that, for every
![]() $j<\theta $
,
$j<\theta $
,
![]() $\{\beta \in E^{\kappa }_{\chi }\mathrel {|} c(\epsilon ,\beta )>j\}$
is stationary. For every
$\{\beta \in E^{\kappa }_{\chi }\mathrel {|} c(\epsilon ,\beta )>j\}$
is stationary. For every
![]() $i<\theta $
, let:
$i<\theta $
, let:
-
•
 $\Gamma _i:=\{\gamma < \kappa \mathrel {|} \epsilon < \gamma \text { and } c(\epsilon ,\gamma )\le i\}$
,
$\Gamma _i:=\{\gamma < \kappa \mathrel {|} \epsilon < \gamma \text { and } c(\epsilon ,\gamma )\le i\}$
, -
•
 $P_i$
denote the collection of all pairs
$P_i$
denote the collection of all pairs
 $(i,f)$
where
$(i,f)$
where
 $f:\kappa \rightarrow 2$
is a partial function of size less than
$f:\kappa \rightarrow 2$
is a partial function of size less than
 $\chi $
.
$\chi $
.
Set
![]() $P:=\{\emptyset \}\cup \biguplus _{i<\theta }P_i$
. Define an ordering
$P:=\{\emptyset \}\cup \biguplus _{i<\theta }P_i$
. Define an ordering
![]() $\le $
of P as follows:
$\le $
of P as follows:
-
(1)
 $\emptyset $
is the top element of
$\emptyset $
is the top element of
 $(P,\le )$
.
$(P,\le )$
. -
(2) For all
 $(i,f),(j,g)\in P\setminus \{\emptyset \}$
, we let
$(i,f),(j,g)\in P\setminus \{\emptyset \}$
, we let
 $(j,g)\le (i,f)$
iff:
$(j,g)\le (i,f)$
iff:-
•
 $i=j$
,
$i=j$
, -
•
 $g \supseteq f$
, and
$g \supseteq f$
, and -
• for all
 $\gamma \in \operatorname {\mathrm {dom}}(f) \cap \Gamma _i$
and
$\gamma \in \operatorname {\mathrm {dom}}(f) \cap \Gamma _i$
and
 $\alpha \in \gamma \cap \operatorname {\mathrm {dom}}(g)\setminus \operatorname {\mathrm {dom}}(f)$
, if
$\alpha \in \gamma \cap \operatorname {\mathrm {dom}}(g)\setminus \operatorname {\mathrm {dom}}(f)$
, if
 $c(\alpha ,\gamma )\le i$
, then
$c(\alpha ,\gamma )\le i$
, then
 $g(\alpha ) = 0$
.
$g(\alpha ) = 0$
.
-
We then let
![]() $\mathbb P:=(P,\le )$
and
$\mathbb P:=(P,\le )$
and
![]() $\mathbb P_i:=(\{\emptyset \}\cup P_i,\le )$
for all
$\mathbb P_i:=(\{\emptyset \}\cup P_i,\le )$
for all
![]() $i<\theta $
.
$i<\theta $
.
Claim 6.3.1.
![]() $\le $
is transitive.
$\le $
is transitive.
Proof Suppose
![]() $(i,h)\le (i,g)$
and
$(i,h)\le (i,g)$
and
![]() $(i,g)\le (i,f)$
. It is clear that
$(i,g)\le (i,f)$
. It is clear that
![]() $h\supseteq f$
. Let
$h\supseteq f$
. Let
![]() $\gamma \in \operatorname {\mathrm {dom}}(f) \cap \Gamma _i$
and
$\gamma \in \operatorname {\mathrm {dom}}(f) \cap \Gamma _i$
and
![]() $\alpha \in \gamma \cap \operatorname {\mathrm {dom}}(h)\setminus \operatorname {\mathrm {dom}}(f)$
with
$\alpha \in \gamma \cap \operatorname {\mathrm {dom}}(h)\setminus \operatorname {\mathrm {dom}}(f)$
with
![]() $c(\alpha ,\gamma )\le i$
. Clearly,
$c(\alpha ,\gamma )\le i$
. Clearly,
![]() $\gamma \in \operatorname {\mathrm {dom}}(g)\cap \Gamma _i$
.
$\gamma \in \operatorname {\mathrm {dom}}(g)\cap \Gamma _i$
.
-
▸ If
 $\alpha \notin \operatorname {\mathrm {dom}}(g)$
, then from
$\alpha \notin \operatorname {\mathrm {dom}}(g)$
, then from
 $(i,h)\le (i,g)$
, it follows that
$(i,h)\le (i,g)$
, it follows that
 $h(\alpha ) = 0$
, as sought.
$h(\alpha ) = 0$
, as sought. -
▸ If
 $\alpha \in \operatorname {\mathrm {dom}}(g)$
, then from
$\alpha \in \operatorname {\mathrm {dom}}(g)$
, then from
 $(i,g)\le (i,f)$
, it follows that
$(i,g)\le (i,f)$
, it follows that
 $h(\alpha ) = g(\alpha )= 0$
, as sought.
$h(\alpha ) = g(\alpha )= 0$
, as sought.
Clearly,
![]() $\mathbb P$
and each of the
$\mathbb P$
and each of the
![]() $\mathbb P_i$
’s are a well-met poset which is
$\mathbb P_i$
’s are a well-met poset which is
![]() $\chi $
-directed closed with greatest lower bounds.
$\chi $
-directed closed with greatest lower bounds.
Claim 6.3.2.
-
(1)
 $\prod _{i < \theta } \mathbb {P}_i$
does not satisfy the
$\prod _{i < \theta } \mathbb {P}_i$
does not satisfy the
 $\kappa $
-cc.
$\kappa $
-cc. -
(2)
 $\mathbb {P}^{\theta }$
does not satisfy the
$\mathbb {P}^{\theta }$
does not satisfy the
 $\kappa $
-cc.
$\kappa $
-cc.
Proof (1) For every
![]() $\alpha <\kappa $
, define
$\alpha <\kappa $
, define
![]() $p_{\alpha }\in \prod _{i < \theta }\mathbb {P}_i$
by setting
$p_{\alpha }\in \prod _{i < \theta }\mathbb {P}_i$
by setting
![]() $p_{\alpha }(i):=(i,\{(\alpha , 1)\})$
for all
$p_{\alpha }(i):=(i,\{(\alpha , 1)\})$
for all
![]() $i<\theta $
. To see that
$i<\theta $
. To see that
![]() $\{p_{\alpha }\mathrel {|} \alpha <\kappa \}$
is an antichain (of size
$\{p_{\alpha }\mathrel {|} \alpha <\kappa \}$
is an antichain (of size
![]() $\kappa $
) in
$\kappa $
) in
![]() $\prod _{i < \theta }\mathbb {P}_i$
, fix arbitrary
$\prod _{i < \theta }\mathbb {P}_i$
, fix arbitrary
![]() $(\alpha ,\gamma )\in [\kappa ]^2$
. Let
$(\alpha ,\gamma )\in [\kappa ]^2$
. Let
![]() $i:=\max \{c(\epsilon ,\gamma ),c(\alpha ,\gamma )\}$
. Then
$i:=\max \{c(\epsilon ,\gamma ),c(\alpha ,\gamma )\}$
. Then
![]() $p_{\alpha }(i)$
and
$p_{\alpha }(i)$
and
![]() $p_{\gamma }(i)$
are incompatible in
$p_{\gamma }(i)$
are incompatible in
![]() $\mathbb {P}_i$
, so
$\mathbb {P}_i$
, so
![]() $p_{\alpha }$
and
$p_{\alpha }$
and
![]() $p_{\gamma }$
are incompatible in
$p_{\gamma }$
are incompatible in
![]() $\prod _{i < \theta }\mathbb {P}_i$
.
$\prod _{i < \theta }\mathbb {P}_i$
.
(2) This follows from Clause (1).
Claim 6.3.3. Let
![]() $j < \theta $
.
$j < \theta $
.
-
(1)
 $\prod _{i < j} \mathbb {P}_i$
is
$\prod _{i < j} \mathbb {P}_i$
is
 $\kappa $
-stationarily layered.
$\kappa $
-stationarily layered. -
(2) If
 $\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then
$\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then
 $\mathbb P^j$
is
$\mathbb P^j$
is
 $\kappa $
-stationarily layered.
$\kappa $
-stationarily layered.
Proof Let
![]() $\mathbb {Q}$
denote
$\mathbb {Q}$
denote
![]() $\prod _{i < j} \mathbb {P}_i$
(resp.
$\prod _{i < j} \mathbb {P}_i$
(resp.
![]() $\mathbb P^j$
). Let
$\mathbb P^j$
). Let
![]() $\Upsilon $
be a regular cardinal with
$\Upsilon $
be a regular cardinal with
![]() $\mathcal {P}_{\kappa }(\mathbb {Q}) \in H_{\Upsilon }$
. Using the fact that
$\mathcal {P}_{\kappa }(\mathbb {Q}) \in H_{\Upsilon }$
. Using the fact that
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\chi $
-inaccessible, construct an
${<}\chi $
-inaccessible, construct an
![]() $\in $
-increasing, continuous sequence
$\in $
-increasing, continuous sequence
![]() $\vec M=\langle M_{\beta } \mathrel {|} \beta < \kappa \rangle $
such that, for all
$\vec M=\langle M_{\beta } \mathrel {|} \beta < \kappa \rangle $
such that, for all
![]() $\beta < \kappa $
:
$\beta < \kappa $
:
-
•
 $M_{\beta } \prec H_{\Upsilon }$
;
$M_{\beta } \prec H_{\Upsilon }$
; -
•
 $|M_{\beta }| < \kappa $
;
$|M_{\beta }| < \kappa $
; -
•
 $\kappa ,\mathbb {Q} \in M_{\beta }$
;
$\kappa ,\mathbb {Q} \in M_{\beta }$
; -
•
 ${^{{<}\chi }}M_{\beta } \subseteq M_{\beta + 1}$
.
${^{{<}\chi }}M_{\beta } \subseteq M_{\beta + 1}$
.
-
▸ If
 $\mathbb {Q}=\prod _{i < j} \mathbb {P}_i$
, then, using our choice of
$\mathbb {Q}=\prod _{i < j} \mathbb {P}_i$
, then, using our choice of
 $\epsilon $
, we fix
$\epsilon $
, we fix
 $\beta \in E^{\kappa }_{\chi }$
with
$\beta \in E^{\kappa }_{\chi }$
with
 $\kappa \cap M_{\beta }=\beta>\epsilon $
such that
$\kappa \cap M_{\beta }=\beta>\epsilon $
such that
 $c(\epsilon ,\beta )>j$
.
$c(\epsilon ,\beta )>j$
. -
▸ If
 $\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then we fix
$\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then we fix
 $\beta \in \partial (c)\cap E^{\kappa }_{\chi }$
with
$\beta \in \partial (c)\cap E^{\kappa }_{\chi }$
with
 $\kappa \cap M_{\beta }=\beta>\epsilon $
.
$\kappa \cap M_{\beta }=\beta>\epsilon $
.
Note that by the continuity of the sequence
![]() $\vec M$
,
$\vec M$
,
![]() ${^{{<}\chi }}M_{\beta } \subseteq M_{\beta }$
. Now, by Fact 6.2, it suffices to prove that
${^{{<}\chi }}M_{\beta } \subseteq M_{\beta }$
. Now, by Fact 6.2, it suffices to prove that
![]() $\mathbb {Q} \cap M_{\beta }$
is a regular suborder of
$\mathbb {Q} \cap M_{\beta }$
is a regular suborder of
![]() $\mathbb {Q}$
. To this end, we will define, for each
$\mathbb {Q}$
. To this end, we will define, for each
![]() $p \in \mathbb {Q}$
, a reduction of p to
$p \in \mathbb {Q}$
, a reduction of p to
![]() $M_{\beta }$
, i.e., a condition
$M_{\beta }$
, i.e., a condition
![]() $p \vert M_{\beta } \in \mathbb {Q} \cap M_{\beta }$
such that, for all
$p \vert M_{\beta } \in \mathbb {Q} \cap M_{\beta }$
such that, for all
![]() $q \leq _{\mathbb {Q}} p \vert M_{\beta }$
with
$q \leq _{\mathbb {Q}} p \vert M_{\beta }$
with
![]() $q \in M_{\beta }$
, q is compatible with p.
$q \in M_{\beta }$
, q is compatible with p.
Fix
![]() $p \in \mathbb {Q}$
. For every
$p \in \mathbb {Q}$
. For every
![]() $\eta < j$
, write
$\eta < j$
, write
![]() $p(\eta )$
as
$p(\eta )$
as
![]() $(i_{\eta },f_{\eta })$
, and set
$(i_{\eta },f_{\eta })$
, and set
![]() $x_{\eta } := \operatorname {\mathrm {dom}}(f_{\eta }) \cap \Gamma _{i_{\eta }} \setminus \beta $
.
$x_{\eta } := \operatorname {\mathrm {dom}}(f_{\eta }) \cap \Gamma _{i_{\eta }} \setminus \beta $
.
Subclaim 6.3.3.1. Let
![]() $\eta <j$
and
$\eta <j$
and
![]() $\gamma \in x_{\eta }$
. Then
$\gamma \in x_{\eta }$
. Then
![]() $D^c_{\leq i_{\eta }}(\gamma )\cap \beta $
is a closed bounded subset of
$D^c_{\leq i_{\eta }}(\gamma )\cap \beta $
is a closed bounded subset of
![]() $\beta $
.
$\beta $
.
Proof As c is closed, it suffices to prove that
![]() $\sup (D^c_{\leq i_{\eta }}(\gamma )\cap \beta )<\beta $
. To avoid trivialities, suppose that
$\sup (D^c_{\leq i_{\eta }}(\gamma )\cap \beta )<\beta $
. To avoid trivialities, suppose that
![]() $\beta \notin \partial (c)$
. So,
$\beta \notin \partial (c)$
. So,
![]() $\mathbb {Q}=\prod _{i < j} \mathbb {P}_i$
and
$\mathbb {Q}=\prod _{i < j} \mathbb {P}_i$
and
![]() $i_{\eta }=\eta $
. Now, as c is subadditive of the second kind,
$i_{\eta }=\eta $
. Now, as c is subadditive of the second kind,
So, since
![]() $c(\epsilon ,\gamma )\le i_{\eta }=\eta <j$
, it follows that
$c(\epsilon ,\gamma )\le i_{\eta }=\eta <j$
, it follows that
![]() $c(\beta ,\gamma )\ge j>i_{\eta }$
. As c is closed, it thus follows that
$c(\beta ,\gamma )\ge j>i_{\eta }$
. As c is closed, it thus follows that
![]() $\{\alpha < \beta \mathrel {|} c(\alpha , \gamma ) \leq i_{\eta }\}$
is bounded below
$\{\alpha < \beta \mathrel {|} c(\alpha , \gamma ) \leq i_{\eta }\}$
is bounded below
![]() $\beta $
.
$\beta $
.
For every
![]() $\eta <j$
, by the subclaim and since
$\eta <j$
, by the subclaim and since
![]() $|x_{\eta }|<\chi $
,
$|x_{\eta }|<\chi $
,
is a well-defined element of
![]() $[\beta ]^{<\chi }$
.
$[\beta ]^{<\chi }$
.
For each
![]() $\eta < j$
, define a partial function
$\eta < j$
, define a partial function
![]() $g_{\eta }:\beta \rightarrow 2$
by letting
$g_{\eta }:\beta \rightarrow 2$
by letting
Clearly,
![]() $g_{\eta }$
has size less than
$g_{\eta }$
has size less than
![]() $\chi $
, so as
$\chi $
, so as
![]() ${^{{<}\chi }}M_{\beta } \subseteq M_{\beta }$
, we have
${^{{<}\chi }}M_{\beta } \subseteq M_{\beta }$
, we have
![]() $(i_{\eta },g_{\eta })\in M_{\beta }\cap P_{i_{\eta }}$
. Define a condition
$(i_{\eta },g_{\eta })\in M_{\beta }\cap P_{i_{\eta }}$
. Define a condition
![]() $p \vert M_{\beta }$
in
$p \vert M_{\beta }$
in
![]() $\mathbb Q$
by letting
$\mathbb Q$
by letting
![]() $(p \vert M_{\beta })(\eta ) := (i_{\eta },g_{\eta })$
for all
$(p \vert M_{\beta })(\eta ) := (i_{\eta },g_{\eta })$
for all
![]() $\eta <j$
.
$\eta <j$
.
As
![]() ${^{{<}\theta }}M_{\beta } \subseteq M_{\beta }$
, we have
${^{{<}\theta }}M_{\beta } \subseteq M_{\beta }$
, we have
![]() $p \vert M_{\beta }\in M_{\beta }\cap \mathbb Q$
. To see that
$p \vert M_{\beta }\in M_{\beta }\cap \mathbb Q$
. To see that
![]() $p \vert M_{\beta }$
is a reduction of p to
$p \vert M_{\beta }$
is a reduction of p to
![]() $M_{\beta }$
, fix
$M_{\beta }$
, fix
![]() $q \leq _{\mathbb {Q}} p \vert M_{\beta }$
in
$q \leq _{\mathbb {Q}} p \vert M_{\beta }$
in
![]() $M_{\beta }$
. The only way that q can fail to be compatible with p is if, for some
$M_{\beta }$
. The only way that q can fail to be compatible with p is if, for some
![]() $\eta < j$
, there are
$\eta < j$
, there are
![]() $\gamma \in x_{\eta }$
and
$\gamma \in x_{\eta }$
and
![]() $\alpha \in \operatorname {\mathrm {dom}}(q(\eta )) \setminus \operatorname {\mathrm {dom}}(f_{\eta })$
such that
$\alpha \in \operatorname {\mathrm {dom}}(q(\eta )) \setminus \operatorname {\mathrm {dom}}(f_{\eta })$
such that
![]() $c(\alpha ,\gamma )\le i_{\eta }$
, but
$c(\alpha ,\gamma )\le i_{\eta }$
, but
![]() $q(\eta )(\alpha ) = 1$
. So suppose
$q(\eta )(\alpha ) = 1$
. So suppose
![]() $\eta $
,
$\eta $
,
![]() $\alpha $
, and
$\alpha $
, and
![]() $\gamma $
are as described. In particular,
$\gamma $
are as described. In particular,
![]() $\alpha $
is smaller than
$\alpha $
is smaller than
![]() $\gamma _{\eta }:=\max (D^c_{\leq i_{\eta }}(\gamma )\cap \beta )$
. As
$\gamma _{\eta }:=\max (D^c_{\leq i_{\eta }}(\gamma )\cap \beta )$
. As
![]() $\gamma _{\eta }\in \operatorname {\mathrm {dom}}(g_{\eta })$
, it thus follows that either
$\gamma _{\eta }\in \operatorname {\mathrm {dom}}(g_{\eta })$
, it thus follows that either
![]() $\gamma _{\eta }\notin \Gamma _{i_{\eta }}$
or
$\gamma _{\eta }\notin \Gamma _{i_{\eta }}$
or
![]() $c(\alpha ,\gamma _{\eta })> i_{\eta }$
. But c is subadditive of the second kind, so
$c(\alpha ,\gamma _{\eta })> i_{\eta }$
. But c is subadditive of the second kind, so
![]() $c(\epsilon ,\gamma _{\eta })\le \max \{c(\epsilon ,\gamma ),c(\gamma _{\eta },\gamma )\}\le i_{\eta }$
and
$c(\epsilon ,\gamma _{\eta })\le \max \{c(\epsilon ,\gamma ),c(\gamma _{\eta },\gamma )\}\le i_{\eta }$
and
![]() $c(\alpha ,\gamma _{\eta })\le \max \{c(\alpha ,\gamma ),c(\gamma _{\eta },\gamma )\}\le i_{\eta }$
. This is a contradiction.
$c(\alpha ,\gamma _{\eta })\le \max \{c(\alpha ,\gamma ),c(\gamma _{\eta },\gamma )\}\le i_{\eta }$
. This is a contradiction.
⊣
Remark 6.4. For infinite regular cardinals
![]() $\theta \leq \chi < \kappa $
such that
$\theta \leq \chi < \kappa $
such that
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\chi $
-inaccessible, for any coloring
${<}\chi $
-inaccessible, for any coloring
![]() $c:[\kappa ]^2\rightarrow \theta $
, the poset
$c:[\kappa ]^2\rightarrow \theta $
, the poset
![]() $\mathbb P$
derived from c in the preceding proof has the following features:
$\mathbb P$
derived from c in the preceding proof has the following features:
-
(1)
 $\mathbb P$
is well-met and
$\mathbb P$
is well-met and
 $\chi $
-directed closed with greatest lower bounds.
$\chi $
-directed closed with greatest lower bounds. -
(2) If c witnesses
 $\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, then for all
$\operatorname {\mathrm {U}}(\kappa ,2,\theta ,2)$
, then for all
 $j<\theta $
,
$j<\theta $
,
 $\mathbb P^j$
is
$\mathbb P^j$
is
 $\kappa $
-cc.
$\kappa $
-cc. -
(3) If c witnesses
 $\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,2)$
, then for all
$\operatorname {\mathrm {U}}(\kappa ,\kappa ,\theta ,2)$
, then for all
 $j<\theta $
,
$j<\theta $
,
 $\mathbb P^j$
has precaliber
$\mathbb P^j$
has precaliber
 $\kappa $
.
$\kappa $
. -
(4) If c is closed, subadditive of the second kind, and
 $\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then for all
$\partial (c)\cap E^{\kappa }_{\chi }$
is stationary, then for all
 $j < \theta $
,
$j < \theta $
,
 $\mathbb {P}^j$
is
$\mathbb {P}^j$
is
 $\kappa $
-stationarily layered.
$\kappa $
-stationarily layered. -
(5)
 $\mathbb P^{\theta }$
is not
$\mathbb P^{\theta }$
is not
 $\kappa $
-cc.
$\kappa $
-cc.
Corollary 6.5. Suppose that
![]() $\kappa $
is
$\kappa $
is
![]() ${<}\theta $
-inaccessible and any one of the following six statements holds.
${<}\theta $
-inaccessible and any one of the following six statements holds.
-
(1)
 $\kappa =\lambda ^+$
and
$\kappa =\lambda ^+$
and
 $\square _{\lambda }$
holds.
$\square _{\lambda }$
holds. -
(2)
 $V = L$
and
$V = L$
and
 $\kappa $
is not weakly compact.
$\kappa $
is not weakly compact. -
(3)
 $\square (\kappa )$
holds after being added generically.Footnote
5
$\square (\kappa )$
holds after being added generically.Footnote
5
-
(4) There exists a
 $\square (\kappa )$
-sequence that avoids a stationary subset of
$\square (\kappa )$
-sequence that avoids a stationary subset of
 $E^{\kappa }_{\theta }$
.
$E^{\kappa }_{\theta }$
. -
(5)
 $\kappa =\lambda ^+$
where
$\kappa =\lambda ^+$
where
 $\lambda $
is a former inaccessible that changed its cofinality to
$\lambda $
is a former inaccessible that changed its cofinality to
 $\theta $
via Prikry/Magidor forcing.
$\theta $
via Prikry/Magidor forcing. -
(6)
 $\theta =\omega $
and
$\theta =\omega $
and
 $\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
holds after being added generically.
$\square ^{\operatorname {\mathrm {ind}}}(\kappa ,\omega )$
holds after being added generically.
Then there is a poset
![]() $\mathbb P$
such that:
$\mathbb P$
such that:
-
•
 $\mathbb {P}$
is well-met and
$\mathbb {P}$
is well-met and
 $\theta $
-directed closed with greatest lower bounds
$\theta $
-directed closed with greatest lower bounds
 $;$
$;$
-
• for all
 $j < \theta $
,
$j < \theta $
,
 $\mathbb {P}^j$
is
$\mathbb {P}^j$
is
 $\kappa $
-stationarily layered
$\kappa $
-stationarily layered
 $;$
$;$
-
•
 $\mathbb {P}^{\theta }$
is not
$\mathbb {P}^{\theta }$
is not
 $\kappa $
-cc.
$\kappa $
-cc.
Proof We will show that any one of the assumptions entails the existence of a closed witness c to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2, \theta , 2)$
such that
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2, \theta , 2)$
such that
![]() $\partial (c)$
is stationary. Then the second bullet point of Theorem 6.3 will furnish the desired poset
$\partial (c)$
is stationary. Then the second bullet point of Theorem 6.3 will furnish the desired poset
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Note first that
![]() $(1) \implies (4)$
and
$(1) \implies (4)$
and
![]() $(2)\implies (4)$
(cf. [Reference Jensen13, Theorem 6.1] or [Reference Devlin10, Theorem VII.1.2’]). In addition, as established in the proof of Theorem 4.15,
$(2)\implies (4)$
(cf. [Reference Jensen13, Theorem 6.1] or [Reference Devlin10, Theorem VII.1.2’]). In addition, as established in the proof of Theorem 4.15,
![]() $(3)\implies (4)$
. Next, by Theorem 4.13(2), if (4) holds, then there is a closed witness c to
$(3)\implies (4)$
. Next, by Theorem 4.13(2), if (4) holds, then there is a closed witness c to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2, \theta , 2)$
for which
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2, \theta , 2)$
for which
![]() $\partial (c)$
is stationary.
$\partial (c)$
is stationary.
The fact that Clause (5) implies the desired conclusion is a consequence of Theorem 4.8 and the fact that Prikry forcing and Magidor forcing do not kill the stationarity of the ground model’s
![]() $E^{\lambda ^+}_{\lambda }$
.
$E^{\lambda ^+}_{\lambda }$
.
It remains to deal with (6). To this end, suppose that
![]() $\vec {C} = \langle C_{\alpha , i} \mathrel {|} \alpha \in \operatorname {\mathrm {acc}}(\kappa ), i(\alpha ) \leq i < \omega \rangle $
is a generically added
$\vec {C} = \langle C_{\alpha , i} \mathrel {|} \alpha \in \operatorname {\mathrm {acc}}(\kappa ), i(\alpha ) \leq i < \omega \rangle $
is a generically added
![]() $\square ^{\mathrm {ind}}(\kappa , \omega )$
-sequence, i.e., V is an extension of some ground model by the forcing from [Reference Lambie-Hanson17, Section 7] to add a
$\square ^{\mathrm {ind}}(\kappa , \omega )$
-sequence, i.e., V is an extension of some ground model by the forcing from [Reference Lambie-Hanson17, Section 7] to add a
![]() $\square ^{\mathrm {ind}}(\kappa , \omega )$
-sequence, and
$\square ^{\mathrm {ind}}(\kappa , \omega )$
-sequence, and
![]() $\vec {C}$
is the sequence generated by the generic filter. Let
$\vec {C}$
is the sequence generated by the generic filter. Let
By [Reference Lambie-Hanson and Rinot22, Claim 3.4.1], S is stationary. Let
![]() $\Gamma := \operatorname {\mathrm {acc}}(\kappa ) \setminus S$
. We now define an
$\Gamma := \operatorname {\mathrm {acc}}(\kappa ) \setminus S$
. We now define an
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \omega )$
-sequence
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \omega )$
-sequence
![]() $\vec {D} := \langle D_{\alpha , i} \mathrel {|} \alpha \in \Gamma , ~ j(\alpha ) \leq i < \omega \rangle $
as follows. For each
$\vec {D} := \langle D_{\alpha , i} \mathrel {|} \alpha \in \Gamma , ~ j(\alpha ) \leq i < \omega \rangle $
as follows. For each
![]() $\alpha \in S$
, let
$\alpha \in S$
, let
![]() $j(\alpha )$
be the least
$j(\alpha )$
be the least
![]() $j \in [i(\alpha ), \omega )$
such that
$j \in [i(\alpha ), \omega )$
such that
![]() $\sup (\operatorname {\mathrm {acc}}(C_{\alpha }, i)) = \alpha $
and, for all
$\sup (\operatorname {\mathrm {acc}}(C_{\alpha }, i)) = \alpha $
and, for all
![]() $j \in [j(\alpha ), \omega )$
, let
$j \in [j(\alpha ), \omega )$
, let
![]() $D_{\alpha , j} := \operatorname {\mathrm {acc}}(C_{\alpha , j})$
. Using our choice of S and the fact that
$D_{\alpha , j} := \operatorname {\mathrm {acc}}(C_{\alpha , j})$
. Using our choice of S and the fact that
![]() $\vec {C}$
is an
$\vec {C}$
is an
![]() $\square ^{\operatorname {\mathrm {ind}}}(\kappa , \omega )$
sequence, it is straightforward to verify that
$\square ^{\operatorname {\mathrm {ind}}}(\kappa , \omega )$
sequence, it is straightforward to verify that
![]() $\vec {D}$
is an
$\vec {D}$
is an
![]() $\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \omega )$
-sequence. By the proof of Theorem 4.4 (cf. also Theorem 4.13) and the fact that
$\boxminus ^{\operatorname {\mathrm {ind}}}(\kappa , \omega )$
-sequence. By the proof of Theorem 4.4 (cf. also Theorem 4.13) and the fact that
![]() $\Gamma \cap S = \emptyset $
, it follows that there is a closed witness c to
$\Gamma \cap S = \emptyset $
, it follows that there is a closed witness c to
![]() $\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2, \omega , 2)$
such that
$\operatorname {\mathrm {U}}^{\operatorname {\mathrm {subadditive}}}(\kappa , 2, \omega , 2)$
such that
![]() $S \subseteq \partial (c)$
.
$S \subseteq \partial (c)$
.
Acknowledgments
The second author was partially supported by the Israel Science Foundation (grant agreement 2066/18) and by the European Research Council (grant agreement ERC-2018-StG 802756).
The results of this paper were presented by the first author at the Kobe Set Theory Workshop 2021, March 2021. Preliminary results of this paper were presented by the second author at the 15th International Luminy Workshop in Set Theory, September 2019. We thank the organizers for the invitations.