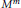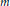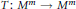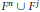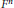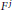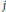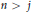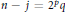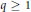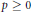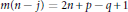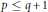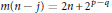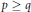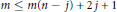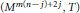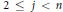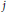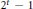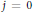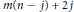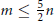Let 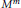 ${{M}^{m}}$ be an
${{M}^{m}}$ be an 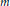 $m$-dimensional, closed and smooth manifold, equipped with a smooth involution
$m$-dimensional, closed and smooth manifold, equipped with a smooth involution 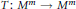 $T\,:\,{{M}^{m}}\,\to \,{{M}^{m}}$ whose fixed point set has the form
$T\,:\,{{M}^{m}}\,\to \,{{M}^{m}}$ whose fixed point set has the form 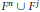 ${{F}^{n}}\,\bigcup \,{{F}^{j}}$, where
${{F}^{n}}\,\bigcup \,{{F}^{j}}$, where 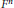 ${{F}^{n}}$ and
${{F}^{n}}$ and 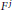 ${{F}^{j}}$ are submanifolds with dimensions
${{F}^{j}}$ are submanifolds with dimensions  $n$ and
$n$ and 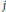 $j$,
$j$, 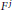 ${{F}^{j}}$ is indecomposable and
${{F}^{j}}$ is indecomposable and 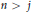 $n\,>\,j$. Write
$n\,>\,j$. Write 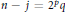 $n\,-\,j\,={{2}^{p}}q$, where
$n\,-\,j\,={{2}^{p}}q$, where 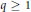 $q\,\ge \,1$ is odd and
$q\,\ge \,1$ is odd and 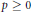 $p\,\ge \,0$, and set
$p\,\ge \,0$, and set 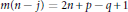 $m(n\,-\,j)\,=\,2n\,+\,p\,-q\,+\,1$ if
$m(n\,-\,j)\,=\,2n\,+\,p\,-q\,+\,1$ if 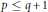 $p\,\le \,q\,+\,1$ and
$p\,\le \,q\,+\,1$ and 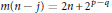 $m(n\,-\,j)\,=\,2n\,+\,{{2}^{p-q}}$ if
$m(n\,-\,j)\,=\,2n\,+\,{{2}^{p-q}}$ if 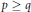 $p\,\ge \,q$. In this paper we show that
$p\,\ge \,q$. In this paper we show that 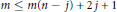 $m\,\le \,m(n-j)+2j+1$. Further, we show that this bound is almost best possible, by exhibiting examples
$m\,\le \,m(n-j)+2j+1$. Further, we show that this bound is almost best possible, by exhibiting examples 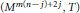 $({{M}^{m(n-j)+2j}},\,T)$ where the fixed point set of
$({{M}^{m(n-j)+2j}},\,T)$ where the fixed point set of  $T$ has the form
$T$ has the form 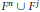 ${{F}^{n}}\,\bigcup \,{{F}^{j}}$ described above, for every
${{F}^{n}}\,\bigcup \,{{F}^{j}}$ described above, for every 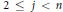 $2\,\le \,j\,<\,n$ and
$2\,\le \,j\,<\,n$ and 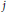 $j$ not of the form
$j$ not of the form 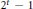 ${{2}^{t}}\,-\,1$ (for
${{2}^{t}}\,-\,1$ (for 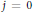 $j\,=\,0$ and 2, it has been previously shown that
$j\,=\,0$ and 2, it has been previously shown that 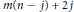 $m(n\,-\,j)\,+\,2j$ is the best possible bound). The existence of these bounds is guaranteed by the famous 5/2-theorem of J. Boardman, which establishes that under the above hypotheses
$m(n\,-\,j)\,+\,2j$ is the best possible bound). The existence of these bounds is guaranteed by the famous 5/2-theorem of J. Boardman, which establishes that under the above hypotheses 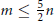 $m\,\le \,\frac{5}{2}\,n$.
$m\,\le \,\frac{5}{2}\,n$.